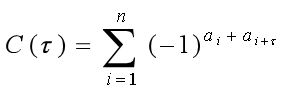现代密码学课程笔记(1)
密码学是一门研究秘密信息的隐写技术的学科,可以使消息的内容对除发送者和接收者以外的所有人保密,可以使接收者验证消息的正确性,是解决计算机与通信安全问题重要技术之一。
密码学历史——代换与置换
- 古典密码:代换与置换
- 代换密码
- 凯撒密码:每个字母用后面的第三个字母替换
Plain: ABCDEFGHIJKLMNOPQRSTUVWXYZ Cipher: DEFGHIJKLMNOPQRSTUVWXYZABC- 一般形式:字母移动位数改为1-25
- 混合表单替换密码:每个字母可以用其他任何一个字母替换(不可重复)——密钥为26个字母
- 简单的单表替换密码
- 写没有重复字母的“密钥字”,其它字母按顺序写在密钥字最后字母后面
- 多字母替换密码
- 一个字母可以被多个字母替换
- 明文下重复写出密钥字,依次使用每个字母作为密钥,加密对应的明文字母
Plaintext:THISPROCESSCANALSOBEEXPRESSED Keyword:CIPHERCIPHERCIPHERCIPHERCIPHE Plaintext:VPXZTIQKTZWTCVPSWFDMTETIGAHLH
- 凯撒密码:每个字母用后面的第三个字母替换
- 置换密码
- 通过重新编排消息字母隐藏信息,没有改变原来消息的子母集
- 按一定规则写出明文,按另一规则读出密文,密钥为读密文的方法和写明文的方法
- 轨道栅栏密码:以不同的行写下消息字母,按行读取消息
- 几何图形密码:一种形式写下消息,以另一种形式读取消息
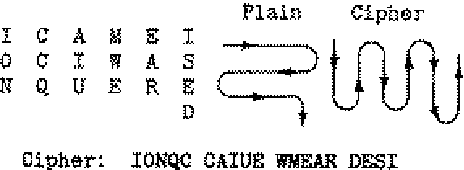
- 行变换密码:按行写出字母,以密钥给出的顺序按行读出密文
- 例:Key(R):读取顺序

- 例:

- 例:Key(R):读取顺序
- 攻击:频率分析;利用常出现的双字母或三字母对,猜测密钥周期,对可能的行列变换进行猜测
- 代换密码
分组密码(对称密码)
对称密码算法:
- 分组密码
- 流密码
私钥加密算法:单钥或对称算法,双方用相同密钥加密/解密
分组密码中,消息被分成许多块,每块都被加密
替换-置换密码
S-P networks
替换(S-boxes):一个二进制字用其他二进制字替换(混淆作用)
- 替换函数为密钥
- 可视为查表运算
- 使明文和密文、密文和密钥之间的统计相关特性极小化,避免统计分析攻击
置换(P-boxes):二进制字次序打乱,重排的方法为密钥(扩散作用),明文和密钥的影响分布到多个密文中
组合:混合变换,一些 S-boxes 由 P-box 连接
Feistel 密码
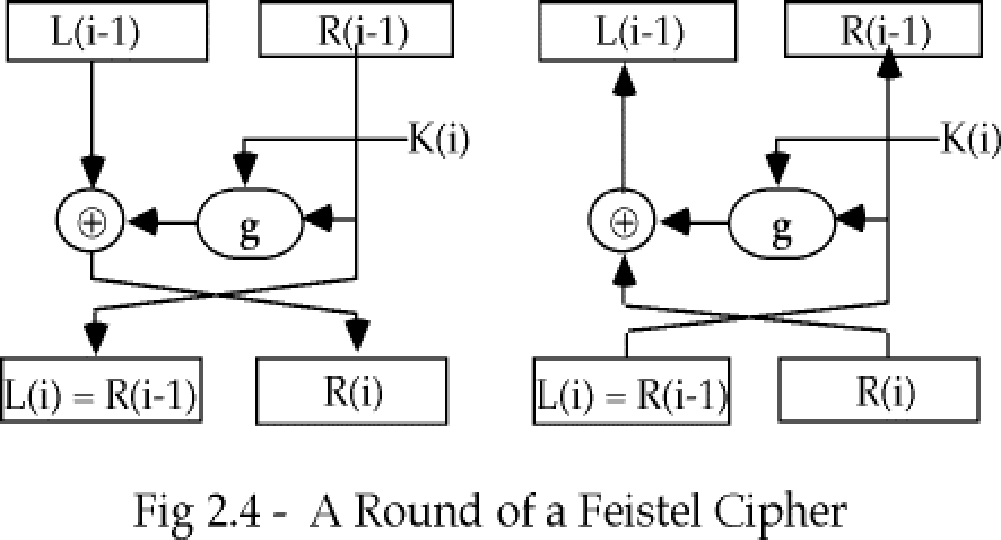
- 输入块分成左右两部分 L(i-1) 和 R(i-1),变换是在密码的第I轮只使用R(i-1)
- g 由第i个密钥K(i)控制
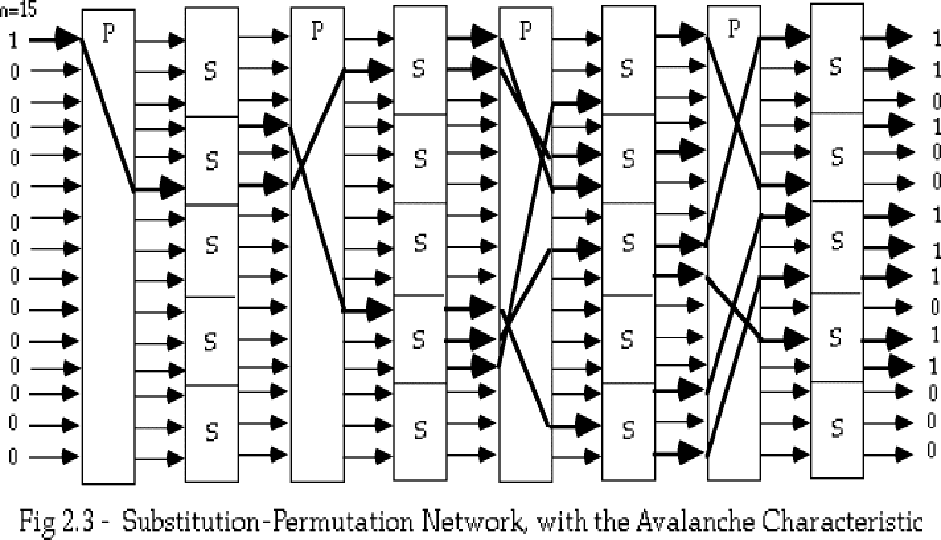
雪崩效应
- 输入改变1bit, 导致近一半的比特发生变化——小的输入变化导致大的输出变化
- 函数$F$有雪崩特性:对$2^m$个明文向量,分为$2^{m-1}$个向量对$x_i$和$x_i’$,每对向量只有一个比特不同,若$V_i=F(x_i)XORF(x_i’)$,则近一半的$V_i$为1
完备性
- 每个输出比特是所有输入比特的复杂函数的输出——每个输出比特依赖于所有输入比特
- 函数$F$有完备性:对每个输出向量的每一比特$j(0<j<m)$,至少存在一个明文对$x_i$和$x_i’$只在第$i$个比特不同,且$F(x_i)$和$F(x_i’)$的第$j$比特不同
Lusifer 密码
DES 前身
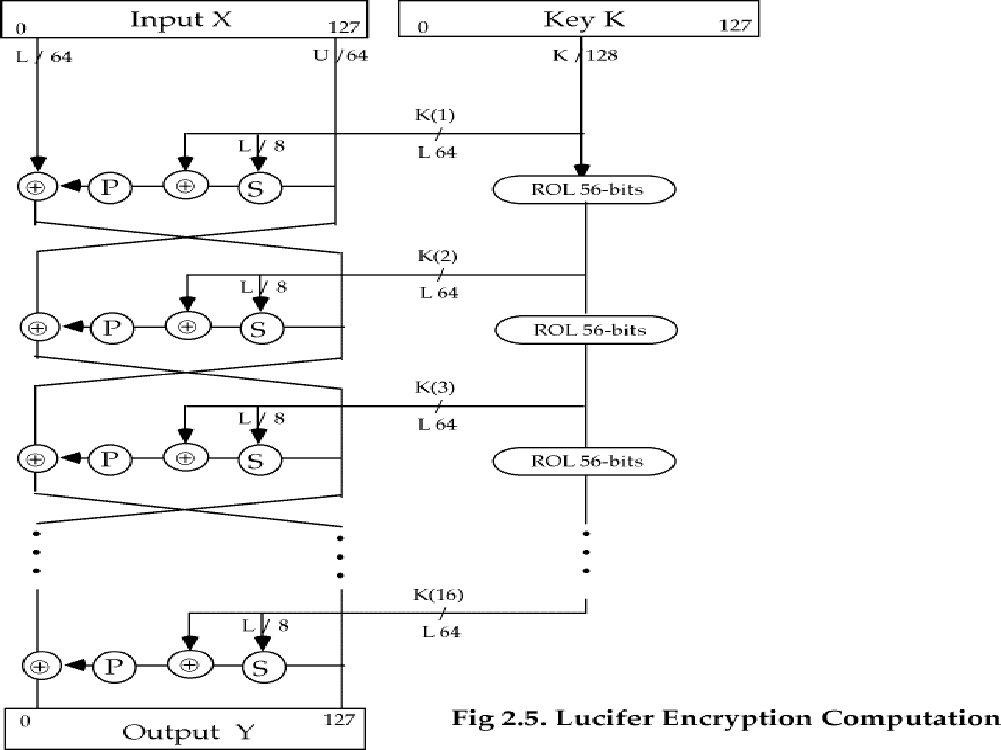
分组长度128bit,密钥长度128bit
16轮,每轮子密钥为密钥左半部分,密钥每次向左旋转56bits
DES
S-DES
五个函数
- 初始置换函数$IP$(initial permutation)
- 复合函数$f_{k1}$,由密钥K确定的,具有转换和替换的运算
- 转换函数$SW$
- 复合函数$f_{k2}$
- 初始置换$IP$的逆置换$IP^{-1}$
流程:
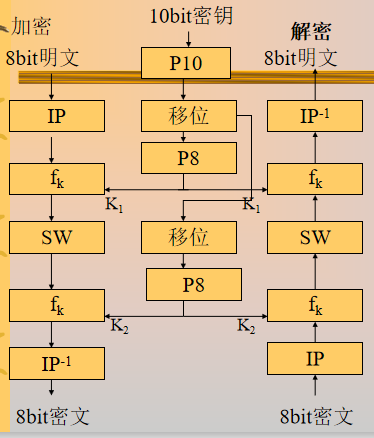
$P10$置换:$P10(k1,k2,…,k10)=(k3,k5,k2,k7,k4,k10,k1,k9,k8,k6)$
$LS-1$为循环左移1位, $LS-2$为循环左移2位
密钥生成:
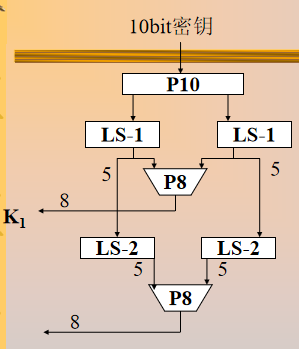
$E/P$:对4位进行扩张和置换运算,(1,2,3,4)变为(4,1,2,3,2,3,4,1)
$S_0$与$S_1$:$S$盒,第一和第四输入比特决定行,第二第三输入比特决定列,以确定选取矩阵元素的位置
加密:
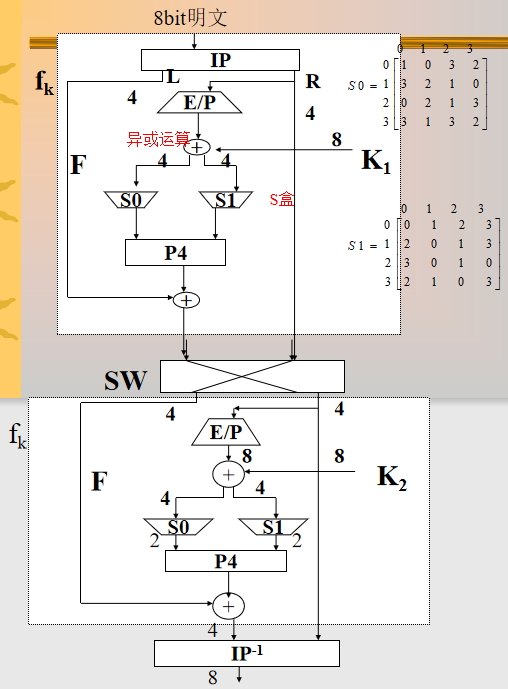
对密钥猜测攻击
DES
分组长度 64 比特,密钥 64(56+8) 比特
过程:

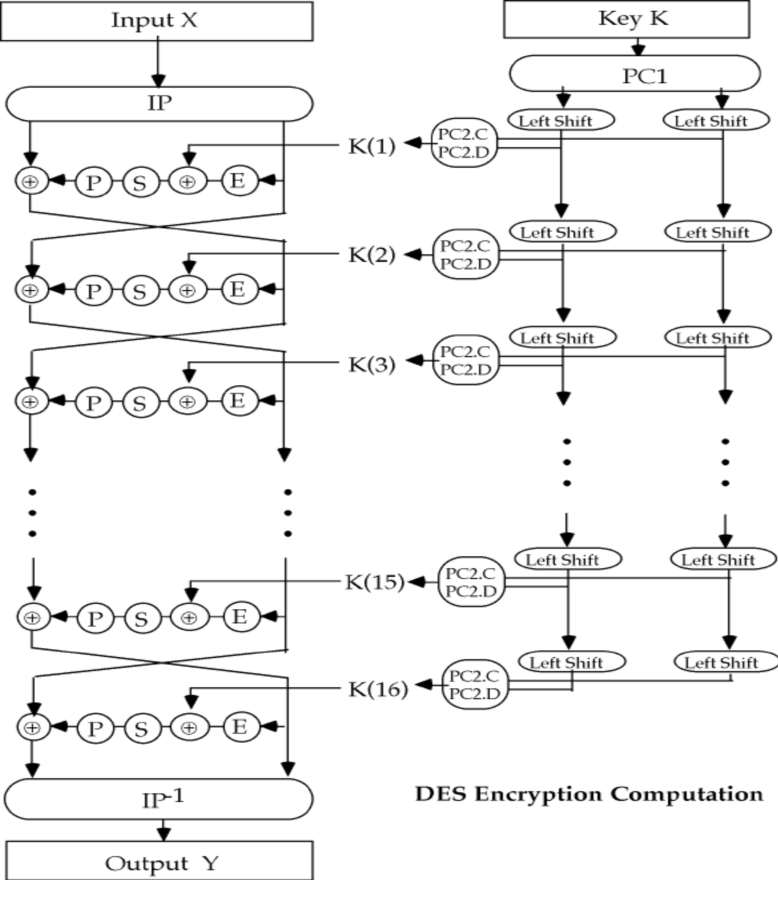
对函数$F$:32bit 通过扩展函数扩展为 48 位;XOR 计算,获得8个6位串;使用 8 个S盒:b1b6确定矩阵行,b2b3b4b5确定矩阵列,得到矩阵元素;通过P固定置换
子密钥:密钥中 56 位参与子密钥编写,8位奇偶校验(不参与密钥编写)
LS:向左循环移位;第1、2、9、16轮移动1位, 其他轮2位
PC-1、PC-2:固定置换56位、48位
每轮获得6*8的表,其中元素对应此轮子密钥使用K的第几比特
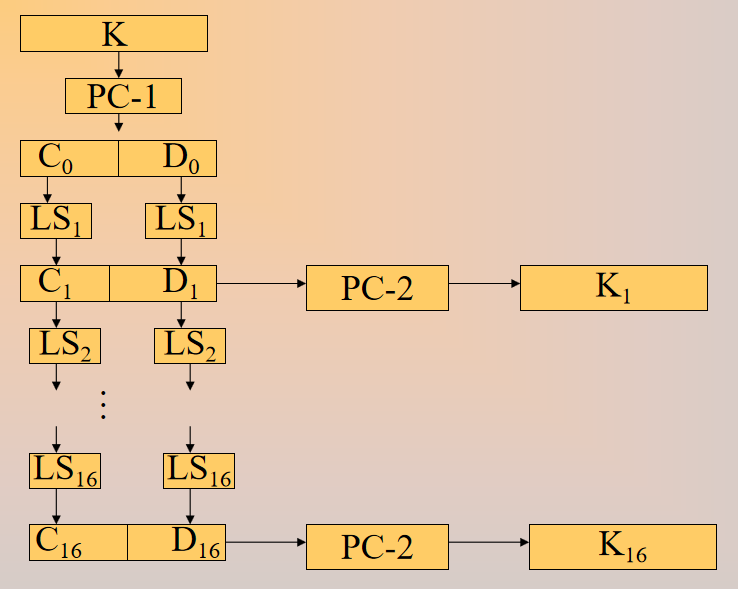
核心是S盒,其他计算是线性的
- S盒不能是线性
- 一个输入改变至少要引起两个输出的改变
- 固定一个输入比特,其他输入变化时,输出数字中0和1近似相等
三重 DES:两个密钥的三重 DES
- $C=E_{K1}[D_{K2}[E_{K1}[P]]]$
- 密钥长度:112
- 不存在$E_{K2}[E_{K1}[P]]=E_{K3}[P]$
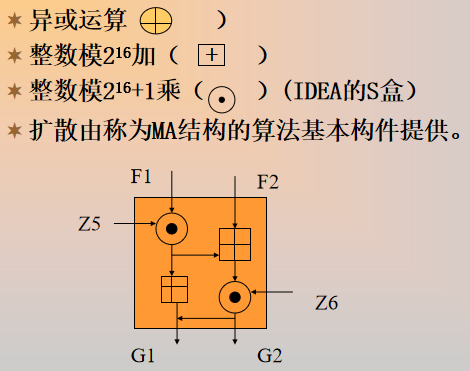
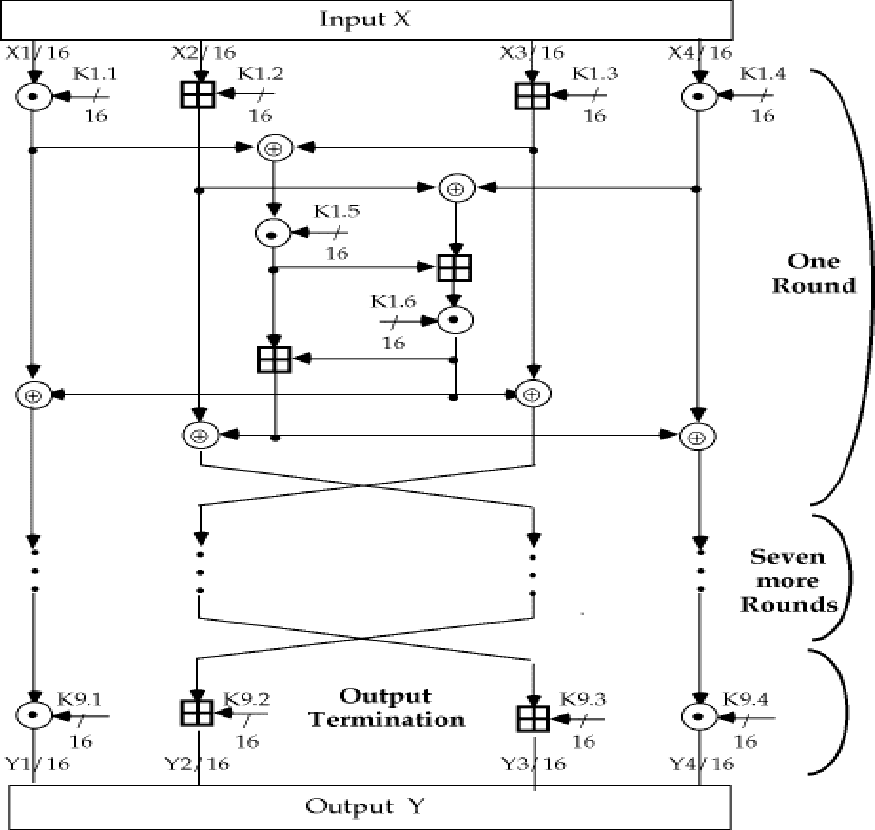
IDEA
抗差分分析和相关分析;PGP的一部分
分组长度 64 位,密钥 128 位,同一算法可加密可解密
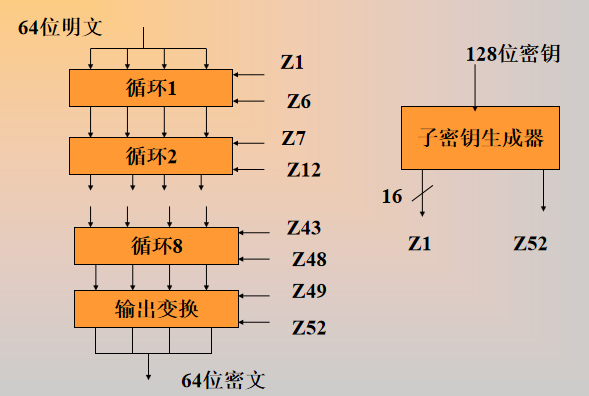
生成 52 个16bit子密钥
- 前8个直接取出
- 25bit循环左移,取出下一个子密钥;重复此过程
解密密钥从加密子密钥导出(对比上一张图理解:共9个循环,前8个每轮需要6个子密钥,最后一轮需要4个子密钥)
解密循环 I 的前4个子密钥从加密循环 10-I 的前4个子密钥导出;解密密钥第1、4个子密钥对应于1、4加密子密钥的乘法逆元;2、3对应2、3的加法逆元;
对前8个循环,循环 I 的最后两个子密钥等于加密循环 9-I 的最后两个子密钥
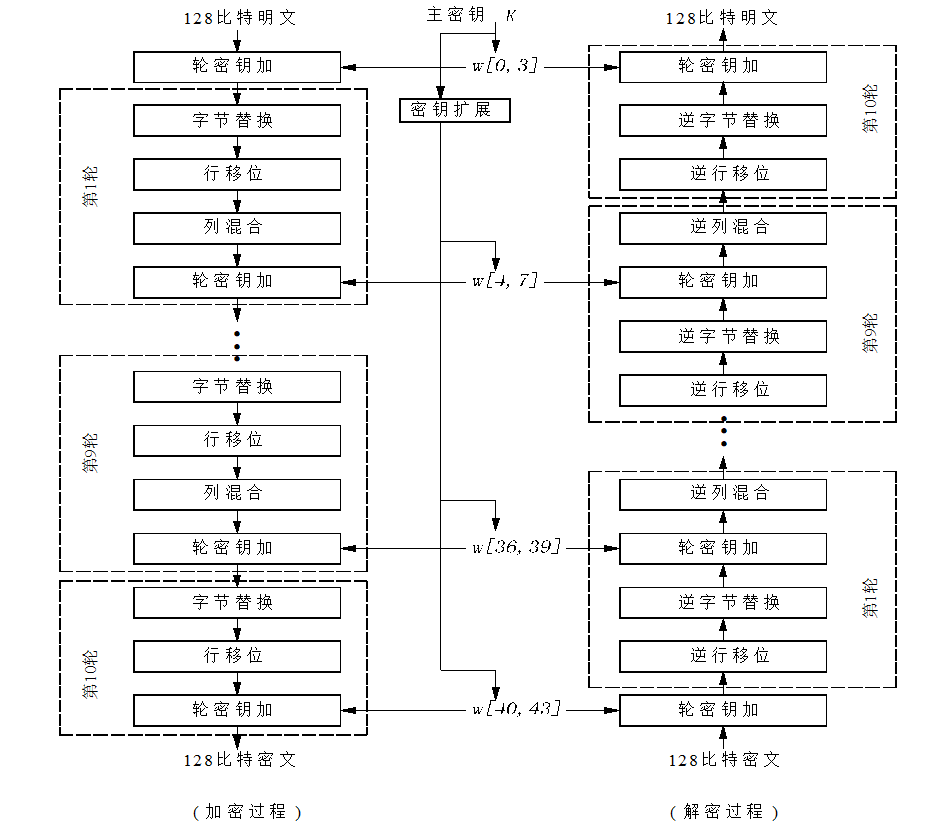
AES
AES框架(Rijndael)
可变块长,可变密钥长度
- 分组长度指定为128位
- 子密钥长度为128,192或256位,128时密钥长1408
- 相应的迭代轮数R为10、12和14
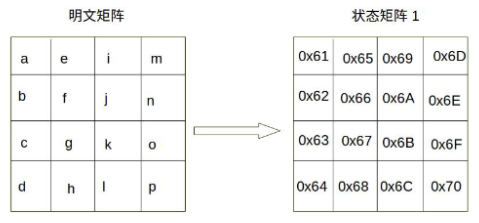
处理单位为字节,明文分组用字节为单位的正方形矩阵表示,称为状态矩阵
明文分组:abcdefghijklmnop
状态矩阵:(0x61为字符a的十六进制表示)
轮函数:
字节替换:每一字节应用非线性变换
- 替代表是一个16*16的矩阵,行来自高4bit,列来自低4bit
行移位:每一行的字节循环重新排序
$B_{i,j}=A_{i,(i+j)mod4}$,即对于4*4的16字节状态矩阵,第一行不移位,第二行左循环移动一位,第三行左循环移动两位,第四行左循环移动三位

列混合:对矩阵的列线性变换(矩阵相乘实现)
移位后的状态矩阵与固定矩阵相乘
加法与乘法时基于$GF(2^8)$的二元运算
- 加法:两个字节异或
- 乘法:乘0x02等价于左移一位,之后同0x1E异或
解密时换一个矩阵

轮密钥加:轮密钥混合到中间数据
将密钥同样变为矩阵形式(32*4),每一列和状态矩阵的同一列进行异或
解密时再进行一次异或
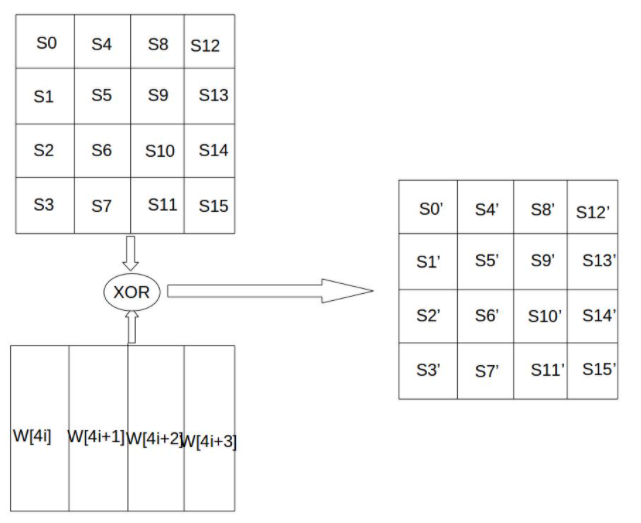
初始密钥输入4*4状态矩阵,即为W[0],W[1],W[2],W[3]
如果i不是4的倍数,则$W[i]=W[i-4]\ XOR\ W[i-1]$
如果i是4的倍数,则$W[i]=W[i-4]\ XOR \ T(W[i-1])$
T:四个字节循环左移1个字节,循环结果用S盒代换,代换结果同4个字节长度的常量进行异或,常量在每一轮都不同
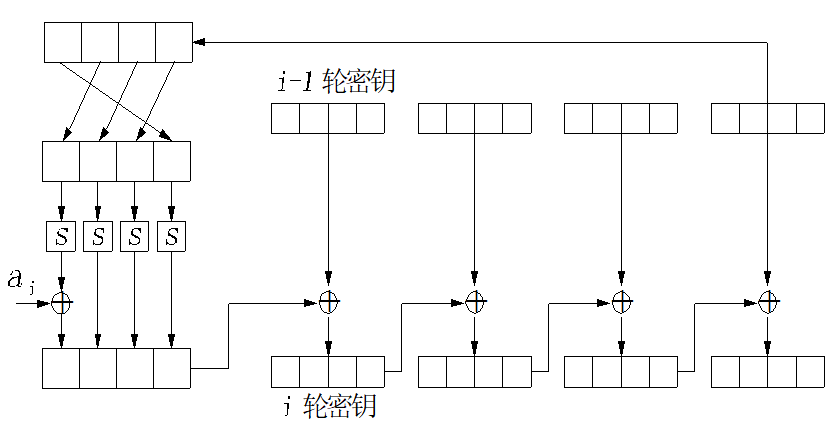
过程:
- 解密对应的字节替换矩阵为逆S盒
分组密码工作模式
DES工作模式:
- Block Modes:ECB, CBC
- Stream Modes :CFB, OFB
ECB(Electronic Code Book)
- 消息分为独立的加密模块,每块单独使用DES加密且密钥相同,适合少量数据的加密
- 少于64bit的消息需要填充
- 同一个64比特明文,如果出现多次,其密文是相同的
CBC(Cipher Block Chaining)
- 没有ECB的缺陷
- 一次对一个明文分组加密,输入为当前明文分组和前一个密文分组的异或,第一个明文加密需要一个初始向量(解密时前一个密文与当前解密结果异或,第一个密文解密需要一个收发双方都知道、被保护的初始向量)
- 可用于用户鉴别
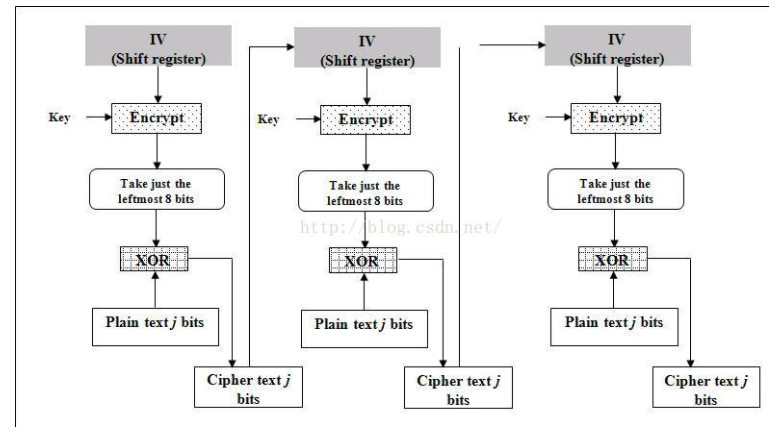
CFB(Cipher FeedBack)
将DES转换为流密码
- 不需要填充消息
- 密文和明文一样长
可用于认证
适合数据以比特或字节为单位,传输过程中比特错误会被传播——1bit错误会影响解密结果中各个明文单元的值
使用一个与块的大小相同的移位寄存器,并用初始向量IV将寄存器初始化;寄存器内容使用块密码加密,结果的最高j比特和对应明文单元(j比特长)异或,获得j位密文;密文移入寄存器最右面j位,并对j比特之后的明文重复此过程
解密过程同上,以密文作为输入
OFB(Output FeedBack)
- 将加密算法的输出(即异或之前的结果)反馈到移位寄存器,CFB将密文单元反馈到寄存器
- 传输过程中比特错误不会被传播
- 缺点:如果对密钥流的一个分组的加密结果和加密前是相同的,这一分组之后的密钥流就会变成同一值的重复
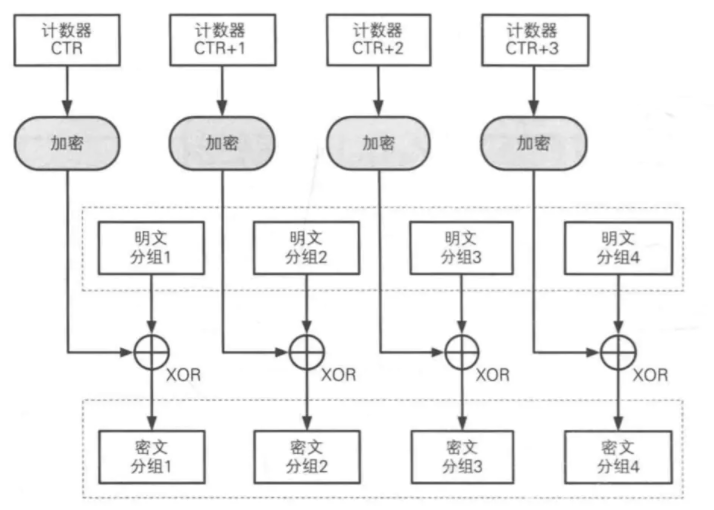
计算器模式(CTR)
- 每个分组对应一个逐次累加的计数器,通过对计数器进行加密来生成密钥流。最终的密文分组是由密钥流和明文分组异或得到
- 以任意顺序处理分组,可并行加密和预处理,吞吐量仅受可使用并行数量的限制
- 无错误传播
- 简单——只要求实现加密算法
对称密码算法分析
- 强力攻击(密钥空间穷搜索)
- 差分密码分析
- 通过分析明文对的差值对密文对的差值影响来恢复某些密钥比特
- 不能破解16轮DES,可破解低轮次
- 不能破解IDEA
序列密码
- 被加密的消息m分成连续的比特串,使用密钥流——向密钥流生成器输入一个密钥(初始密钥/种子),输出伪随机序列——第i个元素对m的第i个元素加密,所有加密输出连接起来形成密文
- 安全性完全取决种子的安全等级
同步流密码与自同步流密码
- 同步流:
- 密钥流与明文串无关
- 实现无错误传播——一个密文字符改变不影响后续符号
- 自同步流:
- 当前密钥流与先前密文有关
线性反馈移位寄存器LFSR
同步密钥流生成方式
反馈函数形如:
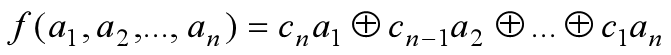
$a_i$为存储单元,取值0/1;n个存储单元称为n级,则有$2^n$个状态;$a_i$与$c_i(c_i=0/1)$相乘后模2加
多项式$c_nx^n+c_{n-1}x^{n-1}+…+c_1x+1$为联接多项式
第$t+1$时刻寄存器的内容为
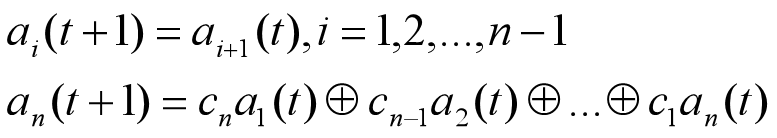
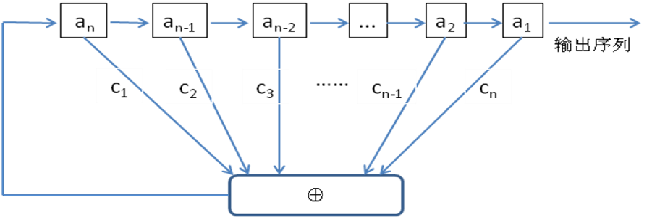
根据联结多项式画LFSR、画状态转移图、算周期
一个n级LFSR序列周期最大为$2^n-1$,若能达到这个周期,则序列为n级最大的线性移位寄存器周期序列,简称m序列,则转移图仅由两个圈构成
- 充要条件为多项式为F2上的n次本原多项式
- $2^n-1$为素数时,每一个不可约多项式都是本原多项式
伪随机序列
- 证明m序列的伪随机性:Golomb 随机性假设
- 在每一周期内,0的个数与1的个数近似相等
- 每一周期内,长度为i的游程数占游程总数的$\frac{1}{2^i}$
- 相关函数为二值函数
线性复杂度
- 序列的线性复杂度:能够输出该序列的最短线性移位寄存器的级数——衡量流密码安全性重要指标
- 序列的线性复杂度为$l$,只要知道序列中任意相继的$2l$位,就可确定整个序列
- 良好的密钥流:周期充分长;随机统计特性好;线性复杂度为序列长度的一半
基于LFSR的伪随机序列生成器
滤波生成器
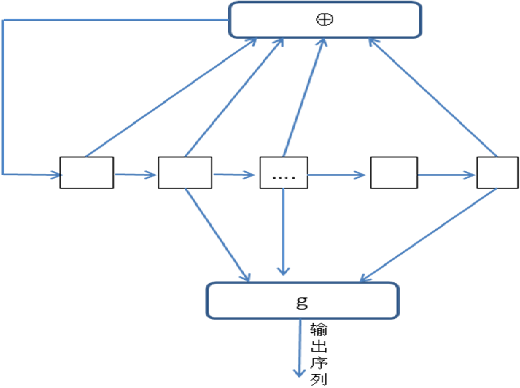
- n级线性移位寄存器+m元非线性滤波函数g,g为m元布尔函数
组合生成器
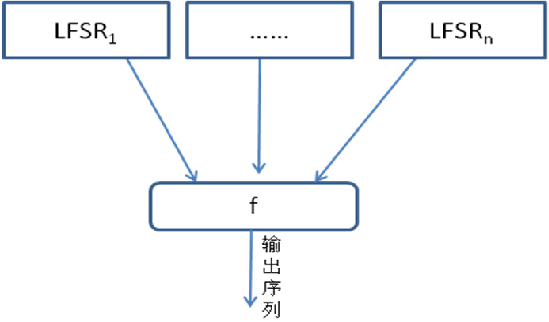
- 若干个线性移位寄存器+非线性组合函数
- 若级数两两互素,f与n个输出都有关,则序列周期为$\prod_{j=1}^n(2^{r_j}-1)$
钟控生成器
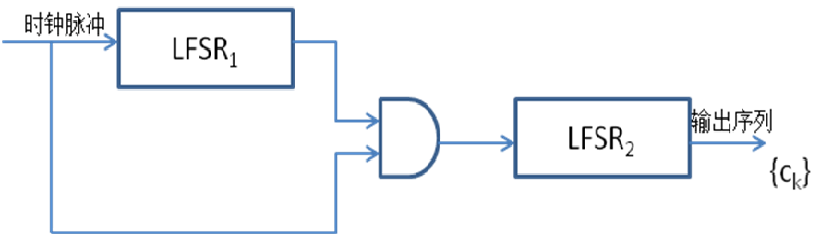
一个或多个移位寄存器来控制另一个或多个移位寄存器的时钟,输出钟控序列
- LFSR1输出1时,时钟脉冲通过与门使LFSR2进行一次移位,生成下一位
- 当LFSR1输出0时,LFSR2重复输出前一位
- LFSR1:10101循环;LFSR2:a0a1a2循环;则:钟控序列为a0a0a1a1a2
交错停走式生成器:LFSR1的输出是1时,LFSR2被时钟驱动;LFSR1的输出是0时,LFSR3被时钟驱动
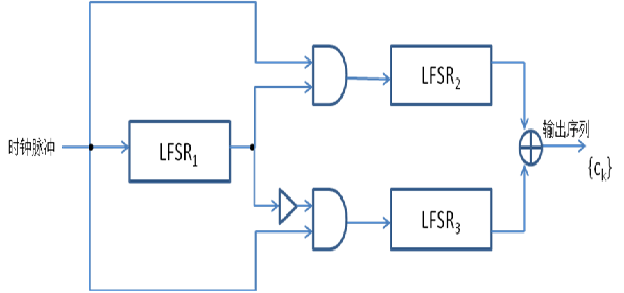
流密码应用
- A5算法:全球移动通信系统GSM中执行加密运算,从用户手机到基站的连接加密
- RC4:密钥长度可变,且面向字节操作