More Than Code

现代密码学（2）公钥密码

发表于 分类于
本文字数： 4.1k 阅读时长 ≈ 4 分钟

现代密码学课程笔记（2）

公钥密码学

  • 对称密码体制缺陷：

    • 密钥分配问题：需要安全信道协商密钥
    • 密钥管理问题：任意两个用户间都要有共享密钥，用户太多则密钥太多
    • 无签名功能：无法向第三方证明来源

  • 理论：

    • 私钥及其他密码信息容易计算公钥
    • 由公钥和算法描述难以计算私钥

  • 安全性：

    • 穷搜索理论上能够破解公钥密码
    • 加密速度慢

  • 公钥分配方案：

    • 不能交换任意消息，可以建立共享密钥
    • 安全性基于离散对数的困难性

  • D-H公钥分配：

    • 初始化
      • 一个大素数p（200位）
      • 一个生成元a
      • 密钥$x_A < p，x_B<p$
      • 计算$y_A=a^{x_A}mod\ p,y_B=a^{x_B}mod\ p$
      • 双方分别公开$y_A,y_B$
    • 计算共享密钥
      • $K_{AB} = (y_A)^{x_B} mod\ p =(y_B)^{x_A} mod\ p$
      • 前者为B的计算，后者为A的计算
    • D-H应用：
      • 抵抗被动攻击,但不能抵抗主动攻击——中间人截获并生成新的私钥、伪造新的公钥，最终发送方接收方以为互相通信，实际上是与中间人通信
      • 主体每次可以选择新的私钥，计算及交换新的公钥

公钥加密算法

基于不同有限域的指数运算：RSA，ElGamal；其他问题的公钥体制大多被攻破

RSA

  • 建立

    • 选择两个随机大素数p，q并计算乘积N、N的欧拉函数$\phi(N)=(p-1)(q-1)$
    • 选择随机数e，e与欧拉函数互素，e为加密密钥
    • 计算d，d满足$ed = 1\ mod\ \phi(N)$
    • 公钥为${e、N}$，私钥为${d、p、q}$
    • 明文M（$M<N$），密文为$C=M^e mod\ N$
    • 解密：$M=C^dmod\ N$

  • e对所有用户可以相同，通常为65535

  • 利用中国剩余定理CRT快速计算

  • 安全性：RSA破译难度不超过大素数分解

    • 共模攻击
    • 低加密指数攻击：e不能太小，短消息要随机数字填充

  • Rabin：对RSA的修正

    • 基于二次剩余问题和模n平方根问题

    • 加密密钥e为2，安全性等价于对n的分解；解密更为困难

    • 不能抵抗选择密文攻击

      • 定理：

        image-20201227164248688

      • 攻击者随机选取一个整数，并计算$m=x^2mod\ n$，骗取签名者对$m$签名，则有0.5的概率从签名$s$和$x$中破解$n$的分解——签名者不知道$x$，则$s\neq \pm x\ mod\ n$，由上面定理可从$gcd(s+x,n)$得到$n$的素因子$p_1$或$p_2$

    • 一个密文对应四个解，其中一个为明文——若M是文字消息则易于识别；若M是随机数字流则无法确定真正的明文

EI Gamal

  • D-H方案的变形，可用于交换密钥；基于离散对数，但增加了消息长度（2倍）
  • 过程：
    • 生成密钥
      • 选取大素数p和本元g
      • 接收方有私钥$x_B$，公开$(y_B=g^{x_B}mod \ p,\ g,\ p)$
    • 加密
      • 明文为M
      • 发送者选取随机数$k$（永久保密）$0\leq k\leq p-1，K=y_B^k mod\ p$
      • 密文对$C={g^kmod\ p,KMmod\ p}$
    • 解密
      • $K=C_1^{x_B}mod\ p,M=C_2K^{-1}mod\ p$

认证与哈希函数

认证函数

  • 认证目的：
    • 防止主动攻击
    • 实体认证——发送者身份，消息认证——消息完整性
  • 攻击：泄露+通信量分析（加密），伪装+内容篡改+序号篡改+计时篡改（消息认证），抵赖（数字签名）
  • 三类认证：消息加密，MAC，哈希函数

消息加密

消息加密提供认证

  • 对称加密：提供保密与一定程度的认证——来自A且没有更改，不提供签名（发送者可否认）
  • 公钥加密：三种情况
    • 接收方公钥（只保密无认证）
    • 发送方私钥（只认证和签名）
    • 接受方公钥+发送方私钥——数字信封

MAC

对选定消息，使用一个密钥，产生一个短小的定长数据分组（认证码），附加在消息中提供认证功能

  • 方法
    • $M || C_k(M)$——认证
    • $E_{k2}(M || C_{k1}(M)$——认证+加密
    • $E_{k2}(M) || C_{k1}(E_{k2}(M))$——认证+加密
  • 适用于消息广播、比加密解密的工作量小、认证与保密分离、延长消息的保护期限
  • 不可逆，且不提供数字签名
  • 性质：
    • 有$M$和 $C_k(M)$，试图生成$M’$，使得$C_k(M’)= C_k(M)$计算上不可行
    • 能均匀分布——$C_k(M)= C_k(M’)$的概率为$2^{-n}$，n为认证码长度——抗选择明文攻击
    • 消息$M’$为$M$的某种已知代换，则$C_k(M)= C_k(M’)$的概率为$2^{-n}$
  • 基于DES的MAC

哈希函数

将任意长度消息映射成一个较短定长输出消息的函数，为文件、消息或其它的分组数据产生“数字指纹”

  • 鉴别方式：
    • $E_k(M || H(M) )$
    • $M || E_k(H(M) )$
    • $M || E_{KRa}(H(M) )$——鉴别与数字签名
    • $E_k(M || E_{KRa}(H(M) ))$
    • $M || H(M || S)$，S为双方共享的一个秘密
    • $E_k(M || H(M || S))$
  • 函数要求：
    • 消息长度任意，输出定长
    • 易于计算
    • 单向性
    • 任意给定分组x，寻求不等于x的y，使得H(y)= H(x)在计算上不可行——弱抗碰撞性
    • 寻求对任何的(x,y)对使得H(x)=H(y)在计算上不可行——强抗碰撞性
  • 用途
    • 检查下载软件的完整性
    • 减少存储空间
    • 数字签名
    • 存储密码
  • 攻击：野蛮攻击，生日攻击

简单的哈希算法

每个n比特长度分组按比特异或，得到长度为n的哈希码

  • 改进：
    • 先将n比特的哈希值设置为0
    • 当前的哈希值循环左移一位
    • 数据分组与哈希值异或形成新的哈希值
  • Merkle-Damgard结构：
    • $M=(Y_0,…,Y_L)，CV_0=初始n比特值$
    • $CV_i=f(CV_{i-1},Y_{i-1}),0<i\leq L$，$f$为压缩函数；如果$f$抗碰撞，则哈希结果抗碰撞
    • $H(M)=CV_L$

MD5

输入任意长度报文，输出128比特的摘要；输入分组长度为512比特；符合Merkle-Damgard结构

img

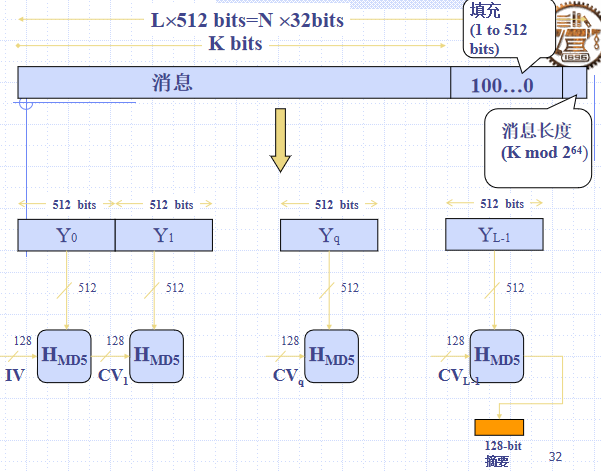
  • 步骤

    • 填充消息，使消息长度为i*512+448比特（i大于0）

    • 添加消息长度（64位）——消息表示为N个32位字

    • 初始化128位MD缓存，存放杂凑中间与最后结果；低端字节存储——低位字节在高地址前

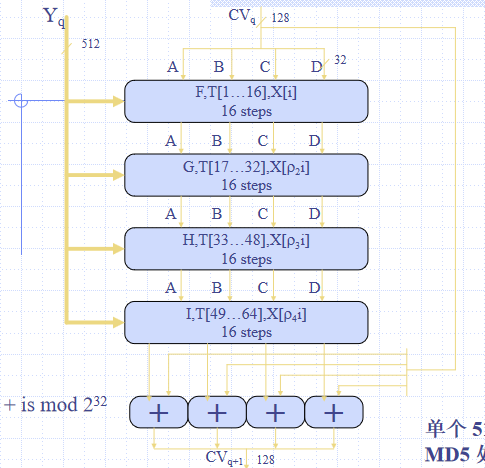
    • 处理报文分组

      • 输入：当前512位分组$Y_q$与上一轮输出$CV_q$

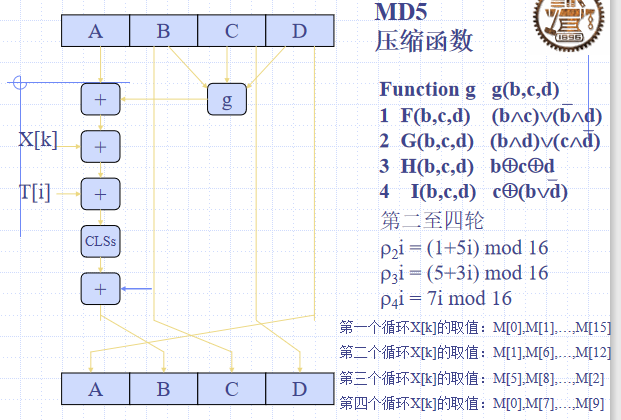
      • 压缩：包含4个循环，顺次记为F，G，H，I；借助列表T[1,…,64]，列表提供随机化的32位模板以消除输入的规律

        • 每个循环包含16步操作

        • 每一步的基本操作：$b \leftarrow b + ((a + g(b, c, d) + X[k] + T[i]) <<< s)$

          • 模$2^{32}$加

          • $a,b,c,d$：MD缓存中的4个字，一开始被初始化，之后每一步操作结果都会替换其中一个字

          • $<<<s$：循环左移s位

          • $T[i]$：矩阵T中的第i个32比特字，i = 1,…,16

          • $g$：循环函数F、G、H、I

          • $X[k]$：当前分组中第k个字

            image-20201212131622648

      • 输出：第四次循环输出加到$CV_q$，得$CV_{q+1}$——模$2^{32}$相加

        image-20201212130317783

  • 应用

    • 生成消息摘要
    • 用于数字签名

  • 逆向

SHA1

输入最大长度为$2^{64}$位的消息，输出160比特，分组为512比特

  • 步骤：

    • 添加填充位，一个1和若干0，使得长度同上

    • 添加消息长度（同上）

    • 初始化160位MD缓冲区，表示为5个字的寄存器；前四个字同MD5；高端字节存储

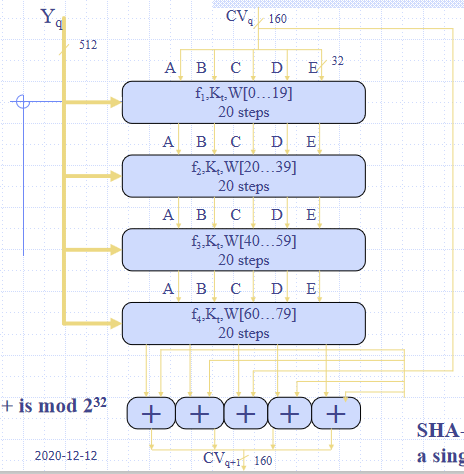
    • 512位数据块为单位，四轮，一轮20步，每轮分别使用一个额外的常数$K_t$

      • 每一步：

        $A,B,C,D,E\leftarrow E+f_t(B,C,D)+S^5(A)+W_i+K_t),A,S^{30}(B),C,D$

        • $f_t$：逻辑函数，每轮循环不同
        • $S^i$：32位常数循环左移$i$位
        • $W_i$：当前512位数据导出的一个32位字；共80个
        • 前16个直接来自当前分组的16个字
          • 其余：$W_t=S^1(W_{t-16}\bigoplus W_{t-14}\bigoplus W_{t-8}\bigoplus W_{t-3})$

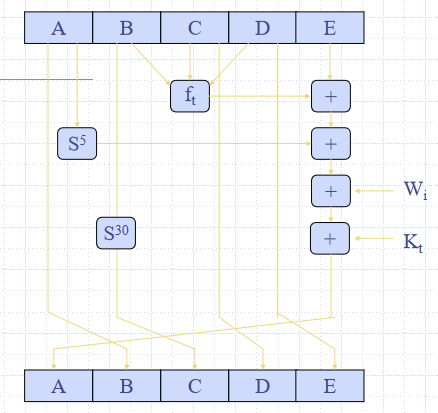
        image-20201212135533253

    • 第四次循环输出加到$CV_q$，得160位$CV_{q+1}$——模$2^{32}$相加

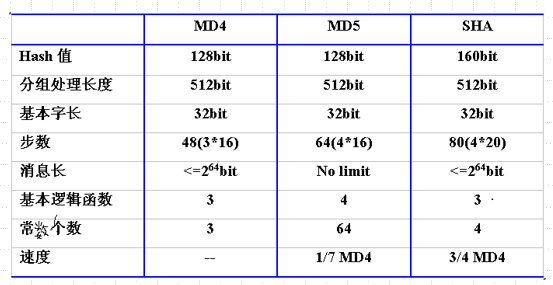
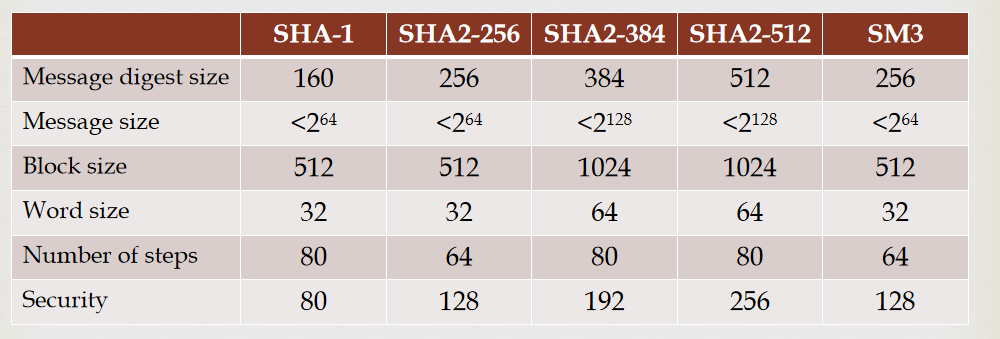
  • 对比

    • SHA = MD4 ＋ 扩展变换 ＋ 外加一轮 ＋ 更好的雪崩（每一轮加上前一步的结果）
    • MD5 = MD4 ＋ 改进的比特杂凑 ＋ 外加一轮 ＋ 更好的雪崩

    image-20201212135015810

    image-20201226134207709

数字签名

只对消息的哈希签名（否则交换信息长度增加一倍）

RSA

已知：${(e,N),(d,p,q)}$

  • 计算明文M的哈希h，$S=h^d(mod\ N)$，发送$(M,S)$
  • 接收方同样计算哈希h，$S^e mod\ N=h’mod\ N$，对比h和h’
  • 若先加密后签名，签名可能被替换

El Gamal

  • 加密算法不可交换——需要专门的签名算法
  • 安全性基于离散对数的计算困难性
  • 公钥：$(y、g、p)$，私钥$(x)$
  • 签名方案
    • 随机数k，与p-1互素
    • $K=g^kmod\ p$
    • $S=k^{-1}(M-Kx)\ mod(p-1)$
    • 发送$(M,K,S)$，销毁k
    • 验证$y^KK^Smod\ p=g^M mod\ p$
  • 签名长度为消息的两倍

DSA

  • El Gamal的变形，生成320位签名
  • 安全性基于离散对数的计算困难性
  • 密钥生成
    • 公开参数$(p,q,g)$
      • p：大素数，$2^L$，L为512到1024位且为64的倍数
      • q：160位（p-1）的素因子
      • g：$h^{(p-1)/q},h<p-1且h^{(p-1)/q}(mod\ p)>1 $
    • 选择私钥x，计算$y=g^xmod\ p$，公钥为$(p,q,g,y)$
  • 签名生成（SHA：哈希函数）
    • $r = (g^k(mod\ p))mod\ q$
    • $s = k^{-1}(SHA(M)+ xr (mod q) )$
    • 发送$(M,r,s)$
  • 签名验证
    • $w = s^{-1}mod\ q $
    • $u1= (SHA(M)w)mod\ q$
    • $u2= rw\ mod\ q$
    • $v = (g^{u1}y^{u2}(mod\ p))mod\ q$
    • 验证$v=r$

HMAC

  • 以上为需要私钥的认证方案，计算量大

  • 密钥与消息同时参加运算：

    $KeyedHash = Hash(Key|Message)$或$Hash(Key1|Hash(Key2|Message))$

  • HMAC：使用带密钥hash函数的结果

    • $HMACK = Hash((K’ \bigoplus opad)||Hash((K’ \bigoplus ipad)||M)) $
    • K’（也为K+）：经过填充的密钥
    • opad、ipad：特殊的填充值

  • 安全性基于原始的hash

相关文章推荐