More Than Code

Faster Password Guessing Using an Ordered Markov Enumerator

发表于 分类于
本文字数： 6.4k 阅读时长 ≈ 6 分钟

《OMEN: Faster Password Guessing Using an Ordered Markov Enumerator》论文阅读记录

摘要

  • 人工生成的密码随机性非常差，这使得它们容易受到猜测攻击
  • 了解对手猜测攻击的能力是评估其影响和提出建议、对策的基本必要条件
  • 介绍了一种新的基于马尔可夫模型的密码破解工具 OMEN，它根据密码候选项的出现概率来生成密码候选项，即首先输出最有可能的密码
  • OMEN 显著提高了猜测速度，在100亿次猜测中正确猜测了80%以上的密码，同比较的所有概率密码破解方法都多
  • OMEN 的性能与 JTR 的马尔可夫模式进行了比较，后者实现了过去的马尔可夫模型功能——最初的9000万次猜测中，OMEN正确猜测了40%以上的密码，后者需要至少8倍的猜测次数才能获得一致的效果

介绍

  • 现状：密码有很高的可移植性，对外行人来说易于理解，对操作员来说易于实施；其他身份验证可以在特定情况下取代密码，但迄今为止，它们还不能大规模取代密码[3]
  • 专注于离线猜测攻击——攻击者只能在愿意投入的时间和资源范围内进行多次猜测
  • JtR 通过对现有的单词字典应用规则进行修改，从现有的数据语料库中生成新的猜测
  • 【24】用 PCFG 从泄露密码库自动提取规则
  • 本文提出了 OMEN，一种新的基于马尔可夫模型的密码破解工具，根据候选密码的出现概率生成候选密码，即首先输出最可能的密码

相关工作

  • 密码以散列形式在服务器存储；破解工作主要由散列函数的计算来完成，因此根据尝试正确猜测密码的次数来评估所有密码破解方法
  • JTR：【17】提出了不同的方法来生成密码。字典模式下，提供一个密码字典作为输入，用户可指定各种规则。对于相对较少的猜测（少于10^8$），字典模式下的 JTR 产生最好的结果。在模式 JtR-inc 中，JTR 基于3元马尔可夫模型尝试破解密码
  • 马尔可夫模型：
    • 【14】对比了不同形式的概率密码模型，并得出结论，马尔可夫模型比概率上下文无关语法更适合估计密码概率——但【14】只是估计了密码的相似性，而没有提出一个具体的密码猜测工具
    • 基本思想：密码中的相邻字母不是独立选择的，而是遵循一定的规律
      • n元马尔可夫模型中，根据长度为 n-1 的前缀对字符串中下一个字符的概率进行建模
      • $P(c_1, . . . , c_m) ≈ P(c_1, . . . , c_{n−1}) ·\prod_{i=n}^mP(c_i|c_{i−n+1}, . . . , c_{i−1})$
      • 模型学习初始概率和转移概率，按照估计的递减概率顺序枚举密码
      • 数据的稀疏性、枚举的最佳顺序是需要考虑的问题
  • PCFG：【24】认为密码具有一定的结构，不同结构的概率从实际的密码中提取，并用于生成猜测密码
  • 密码强度估计：通常，主动密码检查器用于排除弱密码【[22，11，1，18，4】，但大多数主动的密码强度检查工具使用相对简单的规则集来确定口令强度，其效果被证明非常差【23，12，5】。【10】研究了密码策略对密码强度的影响，【2】提出了测量密码强度的新方法。【21】通过限制密码数据库中密码出现的次数来对密码强度进行分类。【5】证明马尔可夫模型可用于安全地衡量密码强度。

OMEN

改进的枚举算法

  • 将所有概率离散成不同的层次，按照递减的顺序遍历。对每一个层次，找与其关联的所有匹配密码

  • 首先获得所有n-gram概率，然后根据$lvl_i= round (log(c_1· prob_i+ c_2))$（$c_1、c_2$使得最频繁的 n-gram 分到0级，而训练中没有出现的 n-gram 也能分到小的概率）将 log 函数处理后的概率离散到不同层次。这里级别是一个参数，可以取值为 0、-1、-2、-3…

  • 给定级别$\eta$和特定长度$l$（假如为3元）

    • 计算所有向量$a=(a_2,…,a_l)$，其中元素为$[0,\eta-1]$之间的整数，且元素之和为$\eta$

    • $P(password) = P(pa)P(s|pa)P(s|as)P(w|ss)P(o|sw)P(r|wo)P(d|or)$

    • 对每一个这样的向量，选择所有二元组$x1x2$，其概率在级别$a_2$中，然后迭代

      image-20210109210300991

OMEN算法

  • 对考虑的所有长度值，执行上面的枚举算法（参数为0，长度值），并计算对应的成功概率
  • 按成功概率降序排列三元组（概率、级别、长度）
  • 删除最高概率的三元组，并执行上面的枚举算法（参数为最高三元组级别-1，最高三元组组长度），获得新的三元组和猜测密码
  • 同样地进行降序排列。重复上面步骤，直到所有三元组都被遍历，或者达到猜测总数

参数选择

  • grams：通常 n 越大效果更好，因为更大的 n 能提供更精确的密码分布估计，但运行时间、内存、空间需求更高。本文对比了 n 为2-5的情况，n=5 的提升比 n=4 的提升小
  • 字符表大小：字符表越大，需要预估越多参数，字符表小则不能生成所有的密码。经过测试，字母表大小为72时，在 Rockyou 测试集上的效果最好
  • 级别：枚举密码候选项的级别数。级别越高，准确率越高。本文结果显示，级别从5增加到10能显著提高准确性，20和30时没有显著提升
  • 4元，字母表为72，10级

评估

数据集

  • Rockyou 数据集：
    • 3260万
    • 大数目能有效训练马尔可夫模型
    • 通过 SQL 注入攻击获得，因此获得了所有的用户，代表性强
    • 分作训练集（RY-t）和测试集（RY-e）
  • MySpace（MS）
    • 50000
    • 来自 2006 年的网络钓鱼攻击
  • Facebook（FB）
    • 2011 年发布
    • 尚不清楚如何获取的
  • 道德审查：
    • 数据集已经被用过
    • 数据集公开
    • 本文只发布几乎不透露实际密码信息的汇总结果

OMEN 与 JTR（马尔可夫模式）

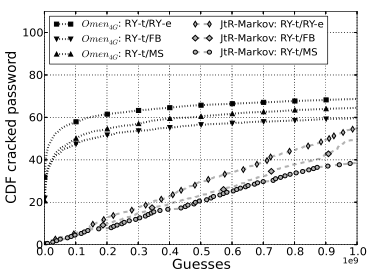
  • 固定猜测次数，并测试覆盖率（OMEN 为4元，JTR-Markov为2元）

  • 曲线显示了破解速度的显著提高，但 JTR-Markov 没有以特定的顺序输出猜测，说明密码可能会在猜测的后期随机出现，因此曲线近似线性

  • 猜测次数更多，JTR-Markov 也不会超过 OMEN。本文对比了猜测次数分别为1和10亿的情况，JTR-Markov的曲线变得更加平缓

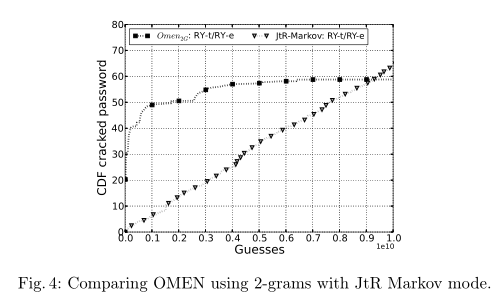
  • 在前一千万次，OMEN 的破解效果更好

  • 设置 OMEN 也为2元后进一步对比，JTR-Markov 仍然为近似为线性

  • 结果

    image-20210109193605696

image-20210109193631327

OMEN 与 PCFG

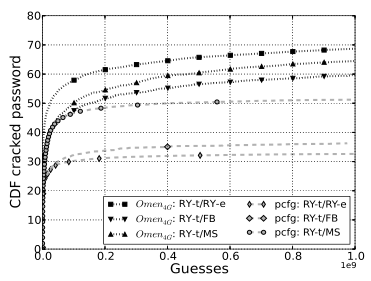
  • 利用【19】的代码：使用RY-t提取语法，使用字典dict-0294 【25】生成候选密码

  • 经过2亿次猜测后，对于 RY-e 和 FB 数据集，OMEN 破解的密码比 PCFG 多20%，ms 多10%——原因可能是 PCFG 的语法是在 MS 的子集上训练的

    image-20210109193020546

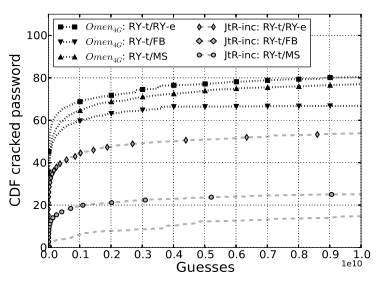
OMEN 与 JtR-inc 模式

  • 同样在 Rockyou 的三千万条密码上训练，在 RY-e、MS、FB 上测试

  • 结果如下

    image-20210109191945907

讨论和结论

  • OMEN 性能优于所有公开的口令猜测工具
  • 100亿次猜测可以猜出80%以上的密码
  • 过去的马尔可夫模型只能按照算法内部规定的顺序输出相应的猜测，与它们的实际频率几乎无关；OMEN 可以近似地按照频率递减顺序输出猜测，从而显著提高现实世界的猜测速度
  • 评估了不同参数对算法精度的影响，并找到了最优参数

参考文献

  1. M. Bishop and D. V. Klein. Improving system security via proactive password checking. Computers & Security, 14(3):233–249, 1995.
  2. J. Bonneau. The science of guessing: analyzing an anonymized corpus of 70 million passwords. In Proc. IEEE Symposium on Security and Privacy. IEEE, 2012.
  3. J. Bonneau, C. Herley, P. C. van Oorschot, and F. Stajano. The quest to replace passwords: A framework for comparative evaluation of web authentication schemes. In Proc. IEEE Symposium on Security and Privacy. IEEE, 2012.
  4. W. E. Burr, D. F. Dodson, and W. T. Polk. Electronic authentication guideline: NIST special publication 800-63, 2006.
  5. C. Castelluccia, M. Dürmuth, and D. Perito. Adaptive password-strength meters from Markov models. In Proc. Network and Distributed Systems Security Symposium (NDSS). The Internet Society, 2012.
  6. M. Dell’Amico, P. Michiardi, and Y. Roudier. Password strength: an empirical analysis. In Proc. 29th conference on Information communications, INFOCOM’10, pages 983–991, Piscataway, NJ, USA, 2010. IEEE Press.
  7. S. Egelman, J. Bonneau, S. Chiasson, D. Dittrich, and S. Schechter. It’s not stealing if you need it: A panel on the ethics of performing research using public data of illicit origin. In Financial Cryptography and Data Security. Springer Berlin Heidelberg, 2012.
  8. HashCat. OCL HashCat-Plus, 2012. http://hashcat.net/oclhashcat-plus/.
  9. G. Kedem and Y. Ishihara. Brute force attack on unix passwords with SIMD computer. In Proc. 8th conference on USENIX Security Symposium - Volume 8, SSYM’99. USENIX Association, 1999.
  10. P. G. Kelley, S. Komanduri, M. L. Mazurek, R. Shay, T. Vidas, L. Bauer, N. Christin, L. F. Cranor, and J. Lopez. Guess again (and again and again): Measuring password strength by simulating password-cracking algorithms. In Proc. IEEE Symposium on Security and Privacy. IEEE, 2012.
  11. D. V. Klein. Foiling the cracker: A survey of, and improvements to, password security. In Proc. USENIX UNIX Security Workshop, 1990.
  12. S. Komanduri, R. Shay, P. G. Kelley, M. L. Mazurek, L. Bauer, N. Christin, L. F. Cranor, and S. Egelman. Of passwords and people: Measuring the effect of password-composition policies. In CHI 2011: Conference on Human Factors in Computing Systems, 2011.
  13. Z. Li, W. Han, and W. Xu. A large-scale empirical analysis of chinese web passwords. In Proc. 23rd USENIX Security Symposium (USENIX Security), Aug. 2014.
  14. J. Ma, W. Yang, M. Luo, and N. Li. A study of probabilistic password models. In Proc. IEEE Symposium on Security and Privacy. IEEE Computer Society, 2014.
  15. R. Morris and K. Thompson. Password security: a case history. Communications. ACM, 22(11):594 – 597, 1979.
  16. A. Narayanan and V. Shmatikov. Fast dictionary attacks on passwords using time space tradeoff. In Proc. 12th ACM conference on Computer and communications security (CCS), pages 364–372. ACM, 2005.
  17. OpenWall. John the Ripper, 2012. http://www.openwall.com/john.
  18. The password meter. Online at http://www.passwordmeter.com/.
  19. PCFG Password Cracker implementation. Matt Weir, 2012. https://sites.google.com/site/reusablesec/Home/password-cracking-tools/probablistic_cracker.13
  20. N. Provos and D. Mazières. A future-adaptive password scheme. In Proc. Annual conference on USENIX Annual Technical Conference, ATEC ’99. USENIX Association, 1999.
  21. S. Schechter, C. Herley, and M. Mitzenmacher. Popularity is everything: a new approach to protecting passwords from statistical-guessing attacks. In Proc. 5th USENIX conference on Hot topics in security, pages 1–8. USENIX Association, 2010.
  22. E. H. Spafford. Observing reusable password choices. In Proc. 3rd Security Symposium, pages 299–312. USENIX, 1992.
  23. M. Weir, S. Aggarwal, M. Collins, and H. Stern. Testing metrics for password creation policies by attacking large sets of revealed passwords. In Proc. 17th ACM conference on Computer and communications security (CCS 2010), pages 162–175. ACM, 2010.
  24. M. Weir, S. Aggarwal, B. de Medeiros, and B. Glodek. Password cracking using probabilistic context-free grammars. In Proc. IEEE Symposium on Security and Privacy, pages 391–405. IEEE Computer Society, 2009.
  25. Word list Collection, 2012. http://www.outpost9.com/files/WordLists.html.
相关文章推荐