Monte Carlo Strength Evaluation：Fast and Reliable Password Checking

《Monte Carlo Strength Evaluation：Fast and Reliable Password Checking》论文阅读记录

摘要

提出了一种新的方法，来估计使用现代攻击查找密码所需的猜测次数
所需资源少，适用于广泛的概率模型，具有很好的收敛性
实验证明了该方案的可扩展性和通用性，并报告了对密码强度的多方向评估，以及对大数据集密码攻击的评估

介绍

【12】表明，在可预见的未来，密码仍然会在大量的场景中应用
密码表鼓励用户选择更好的密码，但它们的输出通常是有问题的，因为它不是对攻击者破解密码所需要工作的可靠评估【6】
密码强度定义为攻击者猜测密码强度所需的尝试次数【1,7,15,18,19,28,29】——猜测策略的基础，并指出可以通过模拟来计算密码强度，但很大一部分未访问密码的强度仍然未知
本文提出一种方法，通过给定的一个攻击模型，评估密码在此模型下的强度
计算效率：采样步骤占用少，可以预先计算；一旦完成，计算密码强度就和通过二分查找一样方便。准确性可以用蒙特卡罗抽样理论描述；对密码强度的估计以速度$O(1/\sqrt{n})$收敛，n是样本中的密码个数
采样100-1000次就已经能够获得正确数量级的猜测次数（密码强度估计），提高采样数目，能够获得更准确的结果
可以用本文的方法评估攻击模型的性能
对于攻击模型，较大的训练集可以改进对“一般”密码的攻击，而对于特别容易或难以猜测的密码，则没有太多效果。而且对于攻击模型的训练，长度要求比有关字符组成的要求更可取
贡献：
- 一种合理的计算密码强度的方法
- 对攻击模型的精度进行了实证评估，包括计算成本和精度之间的权衡
- 一个广泛的经验评估，以比较最新的攻击模型，给出了训练集的影响和密码选择的限制

密码强度评估

最新的密码研究基于概率密码模型，试图在字符串和人类选择字符串作为密码的频率之间建立映射，来描述选择密码的方式
设置所有密码的集合为$\Gamma$，概率密码模型是一个函数$p$，$\sum_{\alpha\in\Gamma} p(\alpha)=1$
攻击模型按概率的降序枚举密码，模型$p$下密码$\alpha$的强度（或秩）$S_{p}（\alpha）$是概率大于$\alpha$的密码数
所有的猜测模型都能实现函数$p$，但如何枚举密码（计算$S_p(\alpha)$）是一个公开的难题【8，21】，但本文的方法只需要采样，不需要实现这个枚举

方法

$\Delta= \begin{Bmatrix} \beta\in\Gamma:p(\beta)>p(\alpha) \end{Bmatrix}\quad$，$\Delta$是强度比$\alpha$弱的密码的集合
采样得到 n 个样本密码，当$n$趋于无穷时，能有效地逼近$S_{p}（\alpha）$
生成 n 个密码的样本集$\theta$，每个密码$\beta$用概率$p（\beta）$采样并替换
**$C_\Delta$为集合$\Delta$的势（度量集合规模大小）为（$\alpha$为需要估计强度的密码） **
为避免概率的上溢和下溢：32位浮点数，使用64位算法
可证明：
- 攻击模型$p$下，$C_\Delta$的期望为$|\Delta|$，等于$S_p(\alpha)$的值
- $C_∆$的方差随样本量增加而减少，收敛速度（标准差）为$O（1/\sqrt{n}）$——蒙特卡罗估计的标准
上面的式子相当于反向的概率加权，即每个元素的贡献乘该元素概率的倒数
【13】在统计中利用了类似的方法

方法优化

以上描述中，每次想要评估密码$\alpha$的强度时从模型$p$采样得到一个大小为$n$的样本$\theta$
优化措施：预计算概率排名曲线，并通过执行$O（log n）$查找来计算新密码的强度，即只需要采样一次并存储数组$A = [p (\beta_1), . . . , p (\beta_n)]$，其中元素降序排列
创建数组$C$：$C[i]=\frac{1}{n}\sum_{j=1}^i\frac{1}{A[j]}=C[j-1]+\frac{1}{nA[j]}$，此时每个$A[i]$和每个$C[i]$对应
计算密码$\alpha$的强度：首先通过二分查找$A[j]>p（\alpha）$中最右边$A[j]$的索引$j$。而对应的$C_\Delta$就等于$C[j]$

实验设置

数据库

Rockyou 数据集
使用 Xato 作为训练集，Rockyou 作为测试集；前者包含了多个密码库，但不包含后者
还交换了二者，结果在很大程度上类似于本文报告的结果——增强了对结果普遍性的信心，证实了两个数据集都没有明显的缺陷，并表明来自使用相同语言的用户的非常大的密码数据集显示出相似的属性
需要明文密码来训练攻击模型和评估强度

攻击模型

N-Grams（n-1阶 Markov 模型）
- 将字符串$c_a…c_b$在训练数据集中出现的次数设置为$o(c_a…c_b)$
- 将字符$c_b$出现在字符串$c_a…c_{b-1}$后面的频率设置为
$$ P(c_b|c_a…c_{b-1}=\frac{o(c_a…c_b)}{o(c_a…c_{b-1})} $$
- 密码$c_1…c_l$的概率为：
$$p_{n-grams}(c_1…c_l)=\prod_{i=1}^{l+1}P(c_i|c_{i-n+1}…c_{i-1})$$
- **$i≤0$或$i>l$时，$c_i$被认为是一个不出现在密码中的特殊符号$\perp$**，表示密码的开始或结束
- 数据稀疏性问题：一些 n-grams 可能训练集中没有，模型会错误地将其概率标记为0——backoff 模型解决了这个问题
- 实现细节：
  - 算法如下图：
  - 设置$c_a…c_{b-1}$为状态$s$，$c_b$为转换$t$，以简化计算
  - 对每个状态$s$，降序排列所有的转换$t_{s,i}$
  - 预计算一个累计概率数组$C_s$，$C_s[i]=\sum_{j=1}^iP(t_{s,j}|s)=C_s[i-1]+P(t_{s,i}|s)$。对此数组可使用二分查找
  - 计算的概率可能非常小，因此存储并计算概率的$log_2$对数，而不是概率本身（后面的方法同样如此）
- 生成的密码按降序排列
PCFG【30】
- 此方法认为，密码通常遵循类似的结构，例如一个单词后跟一个数字。在 PCFG 中，密码按模板分组
- 密码的概率是通过将模板的频率乘以模板中每个模式的频率来计算的，例子如下：
$$p_{PCFG}(“abc123”) = P (L_3D_3) P (“abc”|L_3) P (“123”|D_3)$$
- 从密码训练集中获取模板、数字和符号的频率，并从字典中获取字母组的频率
- 实现细节：
  - 不存储模板和字符组的频率，而是存储它们出现的次数
  - 计算给定密码的概率时，减去由于评估中的密码而导致的一次出现
BackOff【19】
- 通过考虑所有长度的 n-grams 来解决稀疏性，并丢弃出现次数小于阈值$\tau$的那些——对于每一个新字符的选择，模型考虑了前面字符在训练集中出现至少$τ$次的最长序列
- 具体如下图（一个字符的概率是字符在训练集出现的频率）
- 每个密码结尾为$\perp$符号；由于此模型经常生成看上去像后缀的密码，考虑在每个密码前面加上一个开始符号
- 实现细节
  - 简单方法是对训练集进行一次处理，对 n 的任何值计算所有 n-grams 的出现次数，并在处理结束时删除出现次数小于$\tau$的所有 n-grams 的信息
  - 可以迭代处理：第 i 次迭代中，计算 i-grams 的出现次数，丢弃那些少于$\tau$出现次数的 i-grams——本文认为 i-gram 的出现次数不会高于其长度 i-1 的前缀或后缀出现次数
  - 算法如下：

实验结果

评估本文的方法的精度和局限性
比较以上三种攻击模型破解密码的效率
讨论训练集大小对猜测算法性能的影响
评估满足典型限制的密码强度
抽取样本$\theta$为10000；阈值$\tau$为10

方法精度

下图显示了模型计算出密码的概率和对应密码强度$S_{p}(\alpha)$之间关系，这里密码的概率不小于$2^{-20}$。每个模型训练五次，对应的阴影部分为密码强度的范围
- 第一个图表明，估计值接近于正常值，以至于无法辨别阴影区域
- 第二个图对上图某一段做了放大；模型之间的概率结果可能存在差异，因为每个模型生成的密码有不同的概率分布
下图显示在每个$2^{-n}-2^{-n-1}$概率之间的密码比例，显示每个模型都具有非常不同的特征——n-gram 更有可能生成频率低的密码
论文图3证明了先前的收敛定理：样本数目大，则收敛速度快，即相对标准偏差小，而且如果用户只需要密码强度的粗略数量级，那100个样本就够了
图4显示了本文方法的局限性：对于概率非常低的密码，本文的估计是不准确的，因为如果$p(\alpha)$较低则不太可能相似的样本不太可能被采样到，但这种样本对强度估计又十分重要，因为其倒数会给估计结果增加一个很大的值
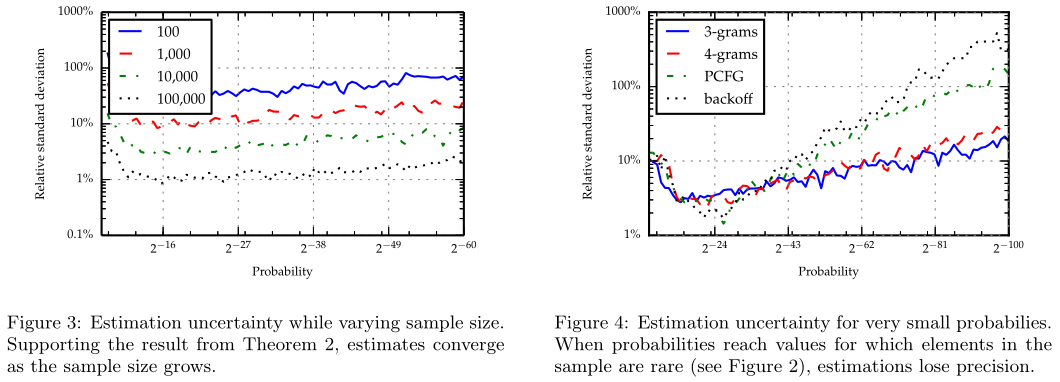
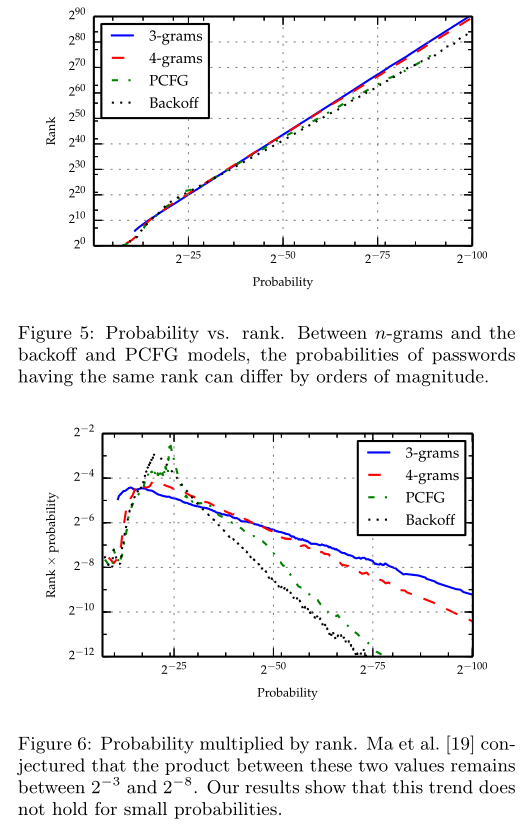
图5显示了，本文的方法相对“以概率评估密码强度”的优势。随着$S_p(\alpha)$的增加，不同模型对$\alpha$的概率值不同，而且会有几个数量级的差异
图6通过$S_p(\alpha)$乘概率值，进一步突出了模型的差异（使图5的差异更为明显）

比较攻击模型

图7绘制了攻击者猜测一个密码的次数和这个密码的概率之间的关系——使用 Xato 作为训练集，通过计算 Rockyou 数据集中的密码获得结果
对于前$2^{16}-2^{20}$个猜测，backoff 和 PCFG 的性能几乎相等：这是因为这两个模型基本上都在猜测训练数据集中最频繁的密码
密码的出现次数低于 BackOff 模型的阈值时，PCFG 模型继续猜测训练集中的单词，而 BackOff 模型开始尝试“泛化”——起初，这有利于 PCFG，但最终 BackOff 模型的效果更好
最佳攻击策略取决于攻击者能够承受的猜测次数
图8分析了不同的攻击是否要经过数目近似的猜测次数，才能猜测到相同的密码（通过绘制散点图）。结果表明，密码抵抗某一攻击的强度表明了密码抵抗其他攻击的强度
N-grams：
- 训练集较大，因此即使使用更高阶的模型（n=3和n=4）也可以找到大部分密码
- 基于 2-grams 和 1-grams 的攻击模型效果较差
PCFG：
- 更好的训练集（Rockyou 而不是 Xato）显著提高了性能
BackOff：
- 使用匹配的数据集作为训练集可以提高攻击效果

训练集的影响

这里只考虑 BackOff 模型，它对于任何次数的尝试都获得了很好的猜测概率
在训练数据集的0.1%到100%之间改变训练集大小
较大的训练集对猜测最简单的密码（最常见的密码可能位于原始训练集的较小子集中）或最难的密码（它们很可能是唯一的，并且即使从较大的训练集中也很少能收集到关于它们的信息）几乎没有影响
提高训练集大小对于“一般”密码（即在较大的数据集中可以找到给定密码或类似的密码）似乎很有用

评估强制性要求

强制要求包括：最小长度、字符组成等
假设攻击者知道此限制，因此不会生成不满足要求的猜测密码
给定一个布尔函数$f(\alpha)$，该函数表示了当前密码是否符合要求，新强度度量应该只计算概率高于$p(\beta)>p(\alpha)$且$f(\beta)$为真的密码
使用 backoff 攻击模型，结果如下：
结果显示，对密码的字符组成做要求不会提高安全性，因为包含字母和数字的密码通常具有可预测的模式；包含特殊符号的密码大约与长度至少为12的密码一样强
结果应被视为对通过实施此类限制可以获得的强度改进的乐观评估

结论

提供了一个可靠的估计——使用最先进的猜测技术对密码进行非常昂贵的攻击的成功率
猜测密码所需的尝试次数与不同的攻击之间存在相关性
应针对几种攻击模型检查用户密码，合理的策略是保守地输出产生最低强度值的结果
相信密码猜测的新发展将很可能继续使用生成概率模型

参考文献

[1] J. Bonneau. The science of guessing: analyzing an anonymized corpus of 70 million passwords. In S&P. IEEE, 2012.

[2] G. Bontempi and S. Ben Taieb. Statistical foundations of machine learning. 2009.

[3] M. Burnett. Today I am releasing ten million passwords. https://xato.net/passwords/ten-million-passwords/, February 2015.

[4] W. Burr, D. Dodson, R. Perlner, W. Polk, and S. Gupta. NIST special publication 800-63-1 electronic authentication guideline, 2006.

[5] C. Castelluccia, M. Dürmuth, and D. Perito. Adaptive password-strength meters from markov models. In NDSS. Internet Society, 2012.

[6] X. de Carn´ e de Carnavalet and M. Mannan. From very weak to very strong: Analyzing password-strength meters. In NDSS. Internet Society, 2014.

[7] M. Dell’Amico, P. Michiardi, and Y. Roudier. Password strength: An empirical analysis. In INFOCOM. IEEE, 2010.

[8] M. Duermuth, F. Angelstorf, C. Castelluccia, D. Perito, and A. Chaabane. OMEN: Faster password guessing using an ordered Markov enumerator. In ESSoS. IEEE, 2015.

[9] S. Egelman, A. Sotirakopoulos, I. Muslukhov, K. Beznosov, and C. Herley. Does my password go up to eleven?: the impact of password meters on password selection. In SIGCHI. ACM, 2013.

[10] D. Florˆ encio, C. Herley, and P. C. Van Oorschot. An administrator’s guide to internet password research. In LISA. USENIX, 2014.

[11] D. Florˆ encio, C. Herley, and P. C. Van Oorschot. Password portfolios and the finite-effort user: Sustainably managing large numbers of accounts. In USENIX Security, 2014.

[12] C. Herley and P. Van Oorschot. A research agenda acknowledging the persistence of passwords. In S&P. IEEE, 2012.

[13] D. G. Horvitz and D. J. Thompson. A generalization of sampling without replacement from a finite universe. J. Am. Stat. Assoc., 47(260):663–685, 1952.

[14] S. Katz. Estimation of probabilities from sparse data for the language model component of a speech recognizer. IEEE TASSP, 35(3):400–401, 1987.

[15] P. G. Kelley, S. Komanduri, M. L. Mazurek, R. Shay, T. Vidas, L. Bauer, N. Christin, L. F. Cranor, and J. Lopez. Guess again (and again and again): Measuring password strength by simulating password-cracking algorithms. In S&P. IEEE, 2012.

[16] D. V. Klein. Foiling the cracker: A survey of, and improvements to, password security. In USENIX Security, 1990.

[17] S. Komanduri, R. Shay, L. F. Cranor, C. Herley, and S. Schechter. Telepathwords: Preventing weak passwords by reading users’ minds. In USENIX Security, 2014.

[18] Z. Li, W. Han, and W. Xu. A large-scale empirical analysis of chinese web passwords. In USENIX Security, 2014.

[19] J. Ma, W. Yang, M. Luo, and N. Li. A study of probabilistic password models. In S&P. IEEE, 2014.

[20] R. Morris and K. Thompson. Password security: A case history. CACM, 22(11):594–597, 1979.

[21] A. Narayanan and V. Shmatikov. Fast dictionary attacks on passwords using time-space tradeoff. In CCS. ACM, 2005.

[22] P. Oechslin. Making a faster cryptanalytic time-memory trade-off. In CRYPTO. Springer, 2003.

[23] C. Percival and S. Josefsson. The scrypt password-based key derivation function. 2012.

[24] W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical Recipes: The Art of Scientific Computing. Cambridge University Press, 3rd edition, 2007.

[25] Solar Designer and S. Marechal. Password security: past, present, future. Passwordˆ12 workshop, December 2012.

[26] E. H. Spafford. Observing reusable password choices. In USENIX Security, 1992.

[27] B. Ur, P. G. Kelley, S. Komanduri, J. Lee, M. Maass, M. L. Mazurek, T. Passaro, R. Shay, T. Vidas, L. Bauer, et al. How does your password measure up? the effect of strength meters on password creation. In USENIX Security, 2012.

[28] R. Veras, C. Collins, and J. Thorpe. On the semantic patterns of passwords and their security impact. In NDSS. Internet Society, 2014.

[29] M. Weir, S. Aggarwal, M. Collins, and H. Stern. Testing metrics for password creation policies by attacking large sets of revealed passwords. In CCS. ACM, 2010.

[30] M. Weir, S. Aggarwal, B. De Medeiros, and B. Glodek. Password cracking using probabilistic context-free grammars. In S&P. IEEE, 2009.

More Than Code

Monte Carlo Strength Evaluation：Fast and Reliable Password Checking

摘要

介绍

相关工作

密码破解

密码强度评估

密码强度评估

方法

方法优化

实验设置

数据库

攻击模型

实验结果

方法精度

比较攻击模型

训练集的影响

评估强制性要求

结论

参考文献