More Than Code

Empirical Analysis of Password Reuse and Modification across Online Service

发表于 分类于
本文字数： 8.1k 阅读时长 ≈ 7 分钟

《Empirical Analysis of Password Reuse and Modification across Online Service》论文阅读记录

摘要

  • 分析了107个服务中2880万用户及其6150万密码
  • 38%的用户在不同的站点重复使用完全相同的密码，而20%的用户修改了现有的密码来创建新的密码
  • 密码修改模式在不同的用户群体中高度一致——密码修改模式具有很高的可预测性
  • 一个新的基于训练的猜测算法——在10次尝试内可以破解1600多万个密码对（30%的修改密码和所有重复使用的密码）

介绍

  • 通过分析公开的密码数据集，试图对用户常用的密码重用/修改方式进行实证测试
  • 开发了一种基于训练的算法，根据目标用户泄露的密码来猜测目标用户的密码
  • 重用频率
    • 38%的用户曾经在两种不同的服务中重用过相同的密码、
    • 21%的用户曾经修改过现有的密码来注册新的服务
    • 电子邮件服务（如Gmail）的密码重用率（60.4%）明显较高
  • 修改密码方式
    • 根据经验测量了8个高级类别的密码转换规则
    • 用户更喜欢使用简单的规则来修改密码
    • 密码转换模式在不同职业和国家的用户中高度一致
  • 攻击者猜测修改后的密码的可能性
    • 基于训练的算法可以在10次尝试内猜出30%的修改密码（100次尝试内46.5%）
    • 即使只训练了0.1%的数据，该算法也能获得相似的性能——密码修改模式的方差低

相关工作

  • 用户遵循简单的转换模式来修改他们的密码，这使得他们的密码是可预测的【8、38】
  • 现有的工作基于用户调查或小规模数据分析（6—7K用户）调查了密码重用和转换【8、15、35、38】
  • 在线密码猜测需要攻击者在有限的尝试次数内猜测密码
  • 基于拖网的方法只是猜测用户选择的最流行密码
  • 大量的工作集中于离线猜【[12-14，21，22，33，36】，尝试的次数是无限的
  • 常见的场景是，给定一个散列密码数据集，脱机猜测将寻求恢复明文密码
    • Markov模型【18、22】
    • 混乱的单词表方法【31】
    • 概率上下文无关文法（PCFGs）【14、22、33、36】
    • 神经网络【21】

数据集

  • 数据集应该包含电子邮件地址，以便跨服务链接用户的密码
  • 很难大规模恢复数据集的密码，因此排除了只包含哈希结果的数据集
  • 总共获得 460874306 个明文密码与 428199842 个唯一用户（占所有密码的93%）。剩下的7%很难用离线猜测工具【2、13、31】恢复，将使用它们来测试猜测算法
  • 需要出现在至少两个网站上的用户——构建了一个包含 28836775 个用户的主数据集，这些用户至少拥有两个明文密码

跨服务重用密码

  • 分析用户为不同服务重用完全相同密码的频率
    • 提取 37301406 密码对，若用户有两个以上的密码，则考虑所有可能的密码对（例如，4个密码意味着6个密码对）
    • 34.3%的密码对相同，38%的用户（1090万）至少有一对相同的密码
  • 拥有更多密码的用户是否更可能重用相同的密码？
    • 密码少于5个的用户，这个假设正确
    • 对于拥有更多密码的用户来说，这种趋势相反——密码越多的用户越有可能为新服务“修改“现有密码
  • 包含电子邮件密码的密码对重用率（60.4%）比总体重用率更高，用户更有可能将其电子邮件密码用于其他服务

密码转换

研究过程如下图：

转换规则

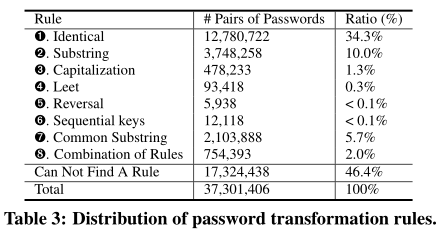
image-20210127184130290

  • 大多数密码对（55.6%）可以用一个转换规则来解释

  • 完全相同：最常见的规则是重复使用相同的密码

  • 子字符串：一个密码是另一个密码的子字符串，此规则匹配 10%。大多数插入/删除发生在尾部，大多数插入/删除的字符串是纯数字（74%）和短字符串

  • 大写：比率不高（1.3%），通常在密码开头大写字母（73%）

  • Leet：0.3%符合 leet 规则。10个变换 leet 变换覆盖了96.6%的 leet 转换密码对

  • 倒转：<0.1% 使用此规则

  • 顺序键：包括字母顺序键（abcd）、顺序号（1234）和键盘上的相邻键。<0.1% 使用此规则

  • 公共子串：要求最长的公共字符串大于2个字符，并且所有的公共子字符串应该覆盖超过 50% 的密码字符。此规则匹配5.7%；本文统计了最长公共子串的典型转换方式，这里一个密码对可能会有多个转换方式

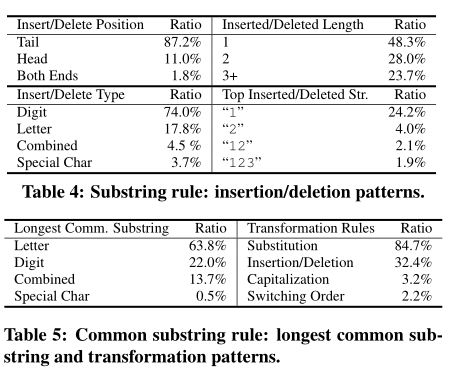
    image-20210127184103796

  • 规则的组合：使用rule3-6的组合首先修改密码，然后测试rule2或rule7是否可以得到匹配结果。此规则匹配了另外2.0%数据

  • 测试了以上所有规则后，仍有46.4%的密码对不匹配——认为46.4%的密码对是用户“从头开始创建新密码”的结果

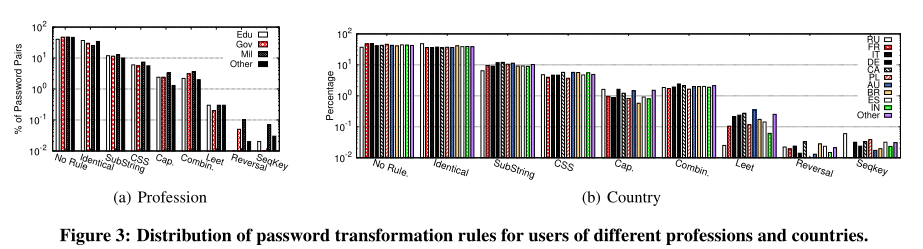
用户人口统计的影响

  • 不同的用户统计数据之间的转换模式的差异——从用户的电子邮件地址推断出他们的人口统计数据
  • 职业
    • 根据邮箱后缀，确定了来自教育机构的128036名用户、来自军队的7376名用户和来自政府的3384名用户
    • 密码转换模式极为相似
  • 国家
    • 识别包含国家代码的邮箱后缀
    • 来自不同国家的用户的转换模式非常相似

image-20210127184020174

密码猜测

猜测算法

  • 针对 DBCBW【8】 中存在的不足，提出了一种新的密码猜测算法

    • DBCBW 通过转换同一用户的已知密码来猜测目标用户密码
    • DBCBW 算法简单，但有两个缺点：第一，缺乏训练数据，该算法使用手工生成的转换规则。第二，以固定的顺序应用这些规则，对于单个密码来说可能不是最优的

  • 学习目标：

    • （1）每个规则的转换过程
    • （2）一个模型来定制每个密码的规则顺序

  • 训练：

    • 训练过程：

      • 对于每个规则$R_i$，我们试图学习密码转换的列表$T_i$
        $$

          T_i=[t_{i1}，t_{i2}，…t_{iN_i}]

        $$
        其中$t_{ij}$表示此规则下的一个转换

      • $T_i$根据每个转换在训练数据集中出现的频率进行排序

      • 密码猜测期间，将独立测试每个转换——“子字符串”规则中，$t$的特征是< insert/delete >< position >< string >，“大写规则”中，$t$的特征是< position >< #chars >

      • “leet”、“顺序键”和“倒转”的转换列表$T$同理

      • “公共子串”：学习排序转换列表（插入、删除、替换、替换、切换顺序）

        • 对于给定的密码，首先分割密码以检测潜在的公共子串
        • 纯数字/字母/特殊字符的子串
        • 英语单词/名称
        • 训练数据中常见的子串

      • “规则的组合”：$T$是规则组合的排序列表，其中每个规则组合都有一个待测试的转换规则排序列表

    • 规则排序：

      • 对于给定的密码，使用贝叶斯模型来学习应该首先应用哪个规则。这视作一个多类分类问题
      • 给定一个密码，训练一个模型来估计密码被每个规则转换的可能性。选择朴素贝叶斯分类器（多项式模型），该模型产生数据点（密码）属于类（规则）的概率；下图为特征

  • 密码猜测

    • 对于给定的密码对（$pw_1$，$pw_2$），测量通过转换已知的$pw2$来测试猜测$pw_1$需要多少次尝试
    • 使用贝叶斯模型为$pw_1$生成一个特定的规则顺序，据此有两个猜测选项：
      • 顺序：一次测试一个规则。在测试了规则下的所有转换之后，转到下一个规则
      • 旋转：一次测试一个规则和一个转换。在根据规则测试一个转换之后，将转到下一个规则来测试另一个转换。轮流测试每一条规则，只做一个猜测
    • 顺序猜测需要更高精度的预测顺序，旋转猜测对预测误差基线的容忍度更高

  • 基准

    • 使用两个基准进行比较
      • 使用固定顺序的规则来“顺序猜测”（类似于DBCBW）
      • 一个流行的现成密码破解工具，开膛手约翰（JtR）【2】。使用 JtR 的“单一”模式并保持默认设置；给定一个密码，JtR 应用一系列规则来转换密码

猜测结果

  • 排除了相同的密码对和没有成对的密码
  • 对50%的数据进行训练，50%数据进行测试：
    • 密码猜测过程中，测试每个密码对的两个方向（$pw_1$→$pw_2$和$pw_2$→$pw_1$）
    • 仅在100次尝试内就猜出46.5%的密码，10次猜测已经破解了30%的密码
    • JtR 基准在前10次尝试中几乎没有破解
    • 贝叶斯模型优于固定排序方法
    • 旋转猜测比顺序猜测要好；顺序猜测的优势在于前5次猜测；通过更频繁地切换规则，旋转猜测具有更好的总体性能
  • 使用更小的训练数据
    • 使用更小的数据集来训练算法（贝叶斯+旋转），以验证转换模式的低方差假设
    • 测试数据不变，训练数据减少到0.1%
    • 0.1%的训练曲线仍然与50%的曲线重叠
  • 破解剩下的哈希密码散列
    • 有6218778个密码对，其中一个密码是未破解的散列，另一个是纯文本的
    • 成功地在5000次尝试中恢复了939400（15.1%）的散列

讨论

  • 考虑到密码的高重用率，有必要通知用户重置密码——被破解的服务，以及具有类似密码的其他服务
  • 在密码重置过程中，应确保用户不修改已泄漏的密码以创建新密码
  • 更好的做法是使用密码管理器为每个服务设置唯一和复杂的密码
  • 电子邮件密码的重复使用率相当高。认为应该向用户发出更具体的警告，以避免在注册服务时重用电子邮件密码

参考文献

[1] Have i been pwned. https://haveibeenpwned.com/.

[2] John the ripper. http://www.openwall.com/john/.

[3] Leet transformation. https://qntm.org/l33t.

[4] Vigilante. https://www.vigilante.pw/.

[5] BAILEY, D. V., DÜRMUTH, M., AND PAAR, C. Statistics on password re-use and adaptive strength for financial accounts. In Proc. of SCN (2014).

[6] BIRD, S., KLEIN, E., AND LOPER, E. Natural Language Processing with Python, 1st ed. O’Reilly Media, Inc., 2009.

[7] CONGER, K. Dropbox employee’s password reuse led to theft of 60m+ user credentials. TechCrunch, 2016.

[8] DAS, A., BONNEAU, J., CAESAR, M., BORISOV, N., AND WANG, X. The tangled web of password reuse. In Proc. of NDSS (2014).

[9] DE CARNÉ DE CARNAVALET, X., AND MANNAN, M. From very weak to very strong: Analyzing password-strength meters. In Proc. of NDSS (2014).

[10] FLORENCIO, D., AND HERLEY, C. A large scale study of web password habits. In Proc. of WWW (2006).

[11] INC., V. 2017 data breach investigations report, 2017.

[12] JI, S., YANG, S., HU, X., HAN, W., LI, Z., AND BEYAH, R. Zero-sum password cracking game: A large-scale empirical study on the crackability, correlation, and security of passwords. IEEE TDSC PP, 99 (2015), 1–1.

[13] JI, S., YANG, S., WANG, T., LIU, C., LEE, W.-H., AND BEYAH, R. Pars: A uniform and open-source password analysis and research system. In Proc. of ACSAC (2015).
[14] KELLEY, P. G., KOMANDURI, S., MAZUREK, M. L., SHAY, R., VIDAS, T., BAUER, L., CHRISTIN, N., CRANOR, L. F., AND LOPEZ, J. Guess again (and again and again): Measuring password strength by simulating password-cracking algorithms. In Proc. of IEEE S&P (2012).

[15] KOMANDURI, S., SHAY, R., KELLEY, P. G., MAZUREK, M. L., BAUER, L., CHRISTIN, N., CRANOR, L. F., AND EGELMAN, S. Of passwords and people: Measuring the effect of password-composition policies. In Proc. of CHI (2011).

[16] LESWING, K. Here’s why linkedin wants you to reset your password. BusinessInsider, 2016.

[17] LI, Y., WANG, H., AND SUN, K. A study of personal information in human-chosen passwords and its security implications. In Proc. of INFOCOM (2016).

[18] MA, J., YANG, W., LUO, M., AND LI, N. A study of probabilistic password models. In Proc. of IEEE S&P (2014).

[19] MANNING, C. D., RAGHAVAN, P., AND SCHÜTZE, H. Introduction to Information Retrieval. Cambridge University Press, 2008.

[20] MAZUREK, M. L., KOMANDURI, S., VIDAS, T., BAUER, L., CHRISTIN, N., CRANOR, L. F., KELLEY, P. G., SHAY, R., AND UR, B. Measuring password guessability for an entire university. In Proc. of CCS (2013).

[21] MELICHER, W., UR, B., SEGRETI, S. M., KOMANDURI, S., BAUER, L., CHRISTIN, N., AND CRANOR, L. F. Fast, lean, and accurate: Modeling password guessability using neural networks. In Proc. of USENIX Security (2016).

[22] NARAYANAN, A., AND SHMATIKOV, V. Fast dictionary attacks on passwords using time-space tradeoff. In Proc. of CCS (2005).

[23] PAGANINI, P. Reuse of login credentials put more than 20m alibaba accounts at risk. Security Affairs, 2016.

[24] PEREZ, R. Hacker publicly releases 900gb of data stolen from cellebrite. SC Magazine, 2017.

[25] PEREZ, S. 117 million linkedin emails and passwords from a 2012 hack just got posted online. TechCrunch, 2016.

[26] RAGAN, S. Mozilla’s bug tracking portal compromised, reused passwords to blame. CSO, 2015.

[27] ROBERTS, J. J. Yahoo could face legal trouble over delay in disclosing hack. Fortune, 2016.

[28] SALINGER, T. Hackers post personal data stolen from adultery website ashley madison to dark web: reports. NY DailyNews, 2015.

[29] SOLON, O. Nhs patient data made publicly available online. Wired, 2014.

[30] UR, B., KELLEY, P. G., KOMANDURI, S., LEE, J., MAASS, M., MAZUREK, M. L., PASSARO, T., SHAY, R., VIDAS, T., BAUER, L., CHRISTIN, N., AND CRANOR, L. F. How does your password measure up? the effect of strength meters on password creation. In Proc. of USENIX Security (2012).

[31] UR, B., SEGRETI, S. M., BAUER, L., CHRISTIN, N., CRANOR, L. F., KOMANDURI, S., KURILOVA, D., MAZUREK, M. L., MELICHER, W., AND SHAY, R. Measuring real-world accuracies and biases in modeling password guessability. In Proc. of USENIX Security (2015).

[32] UR, B., SEGRETI, S. M., BAUER, L., CHRISTIN, N., CRANOR, L. F., KOMANDURI, S., KURILOVA, D., MAZUREK, M. L., MELICHER, W., AND SHAY, R. Measuring real-world accuracies and biases in modeling password guessability. In Proc. of USENIX Security (2015).

[33] VERAS, R., COLLINS, C., AND THORPE, J. On semantic patterns of passwords and their security impact. In Proc. of NDSS (2014).

[34] WANG, D., ZHANG, Z., WANG, P., YAN, J., AND HUANG, X. Targeted online password guessing: An underestimated threat. In Proc. of CCS (2016).

[35] WASH, R., RADER, E., BERMAN, R., AND WELLMER, Z. Understanding password choices: How frequently entered passwords are re-used across websites. In Proc. of SOUPS (2016).

[36] WEIR, M., AGGARWAL, S., MEDEIROS, B. D., AND GLODEK, B. Password cracking using probabilistic context-free grammars. In Proc. of IEEE S&P (2009).

[37] WONG, J. I. Stolen dropbox passwords are circulating online. here’s how to check if your account’s compromised. Quartz, 2016.

[38] ZHANG, Y., MONROSE, F., AND REITER, M. K. The security of modern password expiration: An algorithmic framework and empirical analysis. In Proc. of CCS (2010).

[39] ZHANG-KENNEDY, L., CHIASSON, S., AND VAN OORSCHOT, P. Revisiting password rules: facilitating human management of passwords. In Proc. of eCrime (2016).
相关文章推荐