《Hands-on Machine Learning》第二部分阅读笔记(1)用 tf.keras 训练网络
Introduction to Artificial Neural Networks with Keras
从生物神经元到人工神经元
- 有大量的数据可用于训练神经网络,并且 ANN 在非常大和复杂的问题上经常优于其他最大似然技术
- 计算能力的巨大增长使得在合理的时间内训练大型神经网络成为可能
- 对训练算法进行了改进
- 资金和进步的良性循环
- 一些理论局限性在实践中被证明是良性的
生物神经元
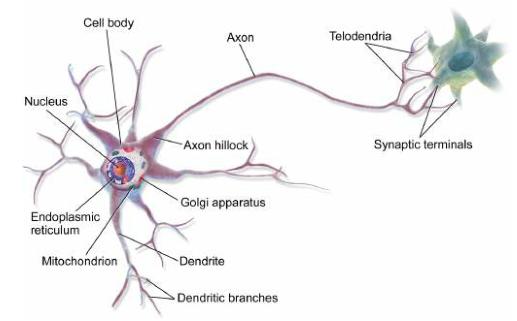
- 高度复杂的计算可以由一个相当简单的神经元组成的巨大网络来完成
- 神经元通常被组织在连续的层中
神经元逻辑计算
- 人工神经元
- 有一个或多个二进制(开/关)输入和一个二进制输出
- 超过一定数量的输入活跃时,人工神经元简单地激活其输出
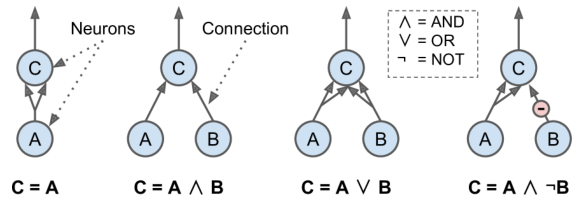
- 第一个网络:神经元 A 被激活,则神经元 C 也被激活
- 第二个网络:只有当神经元 A 和 B 都被激活时,神经元 C 才被激活
- 第三个网络:“或”逻辑
- 第四个网络:稍复杂的逻辑
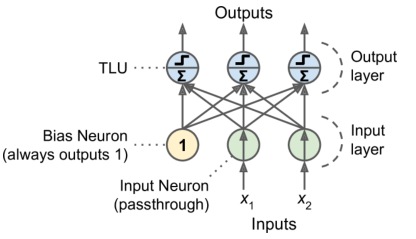
感知器
每个输入连接都与一个权重相关联
计算其输入的加权和
应用阶跃函数并输出结果(即为阈值逻辑单元,TLU)
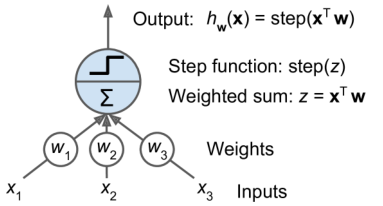
感知器由一个单层的阈值逻辑单元组成
一层中的所有神经元都连接到上一层中的每个神经元(即其输入神经元)时,称为全连接层或密集层
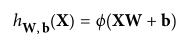
感知器学习算法支持随机梯度下降
感知器不输出类概率
通过堆叠多个感知器可以消除感知器的一些限制
1
2
3
4
5
6
7
8
9
10
11# sklearn 中的感知器
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # petal length, petal width
y = (iris.target == 0).astype(np.int) # Iris Setosa?
per_clf = Perceptron()
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5]])
多层感知器和反向传播
MLP 由一个(直通)输入层、一个或多个被称为隐藏层的 TLU 层和最后一个被称为输出层的 TLU 层组成
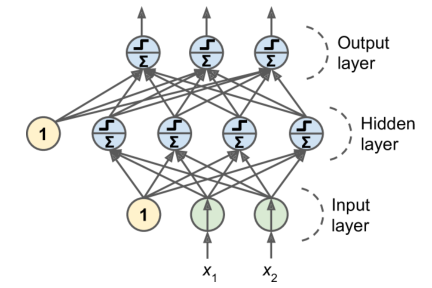
使用一种有效的技术来自动计算梯度——仅仅两次遍历网络,反向传播算法能够计算每个模型参数的网络误差梯度,即找出每个连接权重和每个偏置项应该如何调整
具体算法
- 每次处理一个 batch,一轮称为一个 epoch
- 计算,前向传播,所有中间结果保留下来
- 测量网络的输出误差
- 计算每个输出连接对错误的贡献
- 链式规则测量这些误差中有多少来自下面层的每个连接,以此类推,直到输入层——通过在网络中向后传播误差梯度来建立
- 使用计算的误差梯度调整网络中的所有连接权重
必须随机初始化所有隐藏层的连接权重
替代阶跃函数
- logistic 函数
- tanh(z)
- ReLU(z)
如果层与层之间没有一些非线性变换,即使是一个很深的网络也相当于一个单层
MLP 回归
一般来说,当建立回归的 MLP 时,不对输出神经元使用任何激活函数
- 想保证输出总是正的,可以使用 ReLU
- 保证预测值落在给定的值范围内,可以使用逻辑函数或双曲正切函数,并标签缩放
损失函数通常是均方误差
如果训练集中有很多异常值,使用平均绝对误差

MLP 分类
如果类是排他的,用 softmax
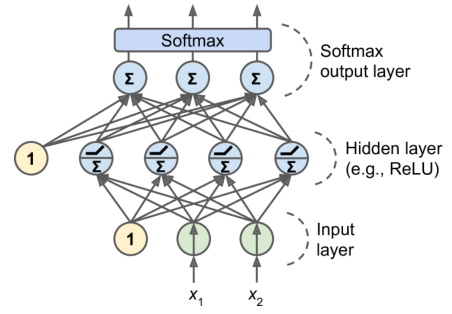

利用 Keras 实现 MLP
- 两种 Keras 实现(keras-team 和 tf.keras)
安装 tf 2.0 并激活
GPU 支持训练,需要安装 tensorflow-gpu
1
2
3
4$ cd $ML_PATH # Your ML working directory (e.g., $HOME/ml)
$ source env/bin/activate # on Linux or MacOSX
$ .\env\Scripts\activate # on Windows
$ python3 -m pip install --upgrade tensorflow-gpu验证:
1
2
3
4
5
6import tensorflow as tf
from tensorflow import keras
tf.__version__
'2.0.0'
keras.__version__
'2.2.4-tf'以下的代码都有:
1
2from tensorflow import keras
output_layer = keras.layers.Dense(10)
Sequential API 实现图像分类
数据加载
1
2fashion_mnist = keras.datasets.fashion_mnist
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()- 创建验证集,并转换像素范围
1
2X_valid, X_train = X_train_full[:5000] / 255.0, X_train_full[5000:] / 255.0
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]- 分类字典
1
2class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
"Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]创建模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))
# 或者
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="relu"),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])summary()打印模型的层信息可以得到一个模型的层列表,通过索引或层的名字来获取一个层
1
2
3
4
5
6
7
8
9model.layers
[<tensorflow.python.keras.layers.core.Flatten at 0x132414e48>,
<tensorflow.python.keras.layers.core.Dense at 0x1324149b0>,
<tensorflow.python.keras.layers.core.Dense at 0x1356ba8d0>,
<tensorflow.python.keras.layers.core.Dense at 0x13240d240>]
model.layers[1].name
'dense_3'
model.get_layer('dense_3').name
'dense_3'get_weights()和set_weights()可以访问层的所有参数1
weights, biases = hidden1.get_weights()
可以在创建层时设置
kernel_initializer与bias_initializer实现初始化,否则会随机初始化权重使用“稀疏_分类_交叉”损失,因为有稀疏标签——对于每个实例,只有一个目标类索引,并且类是排他的——如果对于每个实例,每个类都有一个目标概率,例如一个独热向量,则需要使用“分类_交叉熵”损失
训练与评估
使用
fit()训练1
history = model.fit(X_train, y_train, epochs=50, validation_data=(X_valid, y_valid))
如果训练集非常倾斜,有些类的代表比例过高,而其他类的代表比例过低,需要设置
class_weight参数,给代表比例过高的类一个较低的权重如果需要实例的权重(某些实例为专家标注,其他为众包平台标记,前者需要更大权重),设置参数
class_weight利用 history 绘图
1
2
3
4
5import pandas as pd
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1) # set the vertical range to [0-1]
plt.show()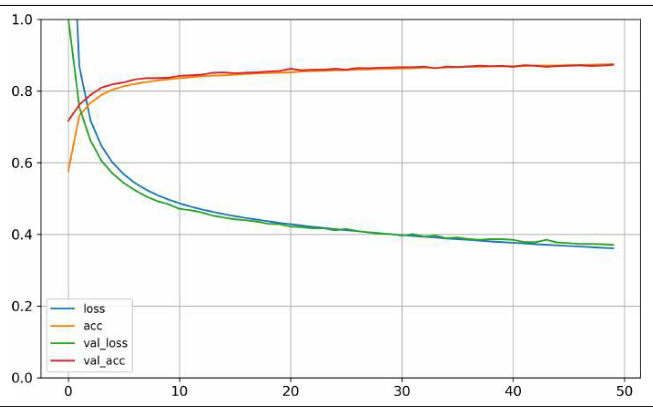
使用
model.evaluate(X_test, y_test)评估使用
model.predict(X_new).round(2)预测
Sequential API 实现回归
用
sklearn加载数据集1
2
3
4
5
6
7
8
9
10
11
12from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
X_test_scaled = scaler.transform(X_test)数据集噪音较大,因此只用一个隐层且限制神经元数目,避免过拟合
1
2
3
4
5
6
7
8
9
10model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]),
keras.layers.Dense(1)
])
model.compile(loss="mean_squared_error", optimizer="sgd")
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
X_new = X_test[:3] # pretend these are new instances
y_pred = model.predict(X_new)
函数 API 实现复杂模型
非顺序神经网络的一个例子是宽深度神经网络,将所有或部分输入直接连接到输出层,学习深度模式(使用深度路径)和简单规则(通过短路径)
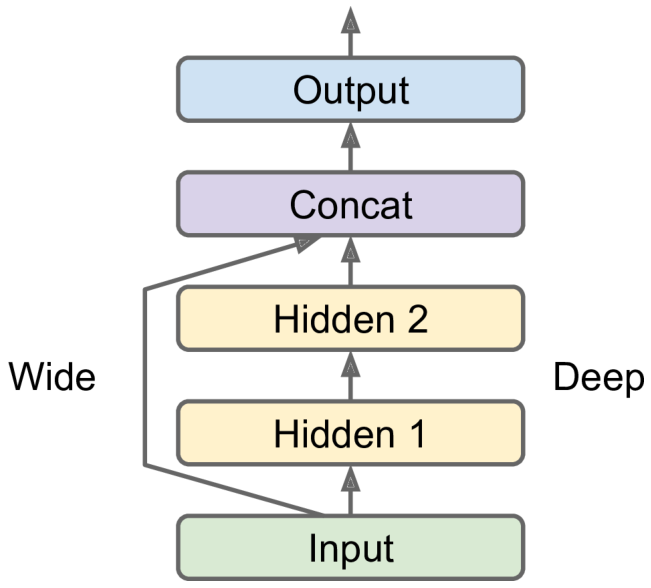
实现上面的预测网络
1
2
3
4
5
6input = keras.layers.Input(shape=X_train.shape[1:]) # 创建一个输入对象
hidden1 = keras.layers.Dense(30, activation="relu")(input) # 创建一个密集层,并像调用一个函数一样调用它,把输入传递给它
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.Concatenate()([input, hidden2]) # 创建一个Concatenate()层,连接第二个隐藏层的输出和输入
output = keras.layers.Dense(1)(concat) # 创建输出层
model = keras.models.Model(inputs=[input], outputs=[output])如果存在多个输入:
1
2
3
4
5
6
7input_A = keras.layers.Input(shape=[5])
input_B = keras.layers.Input(shape=[6])
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1)(concat)
model = keras.models.Model(inputs=[input_A, input_B], outputs=[output])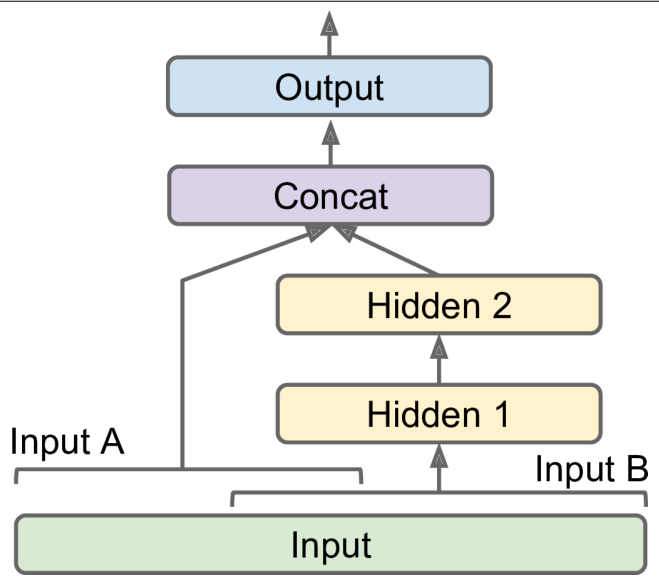
- 此时,调用
fit()方法时,必须传递一对矩阵(X_train_A,X_train_B)
- 此时,调用
如果存在多个输入和输出:
1
2
3
4
5
6
7
8
9
10
11
12
13
14[...] # Same as above, up to the main output layer
output = keras.layers.Dense(1)(concat)
aux_output = keras.layers.Dense(1)(hidden2)
model = keras.models.Model(inputs=[input_A, input_B],
outputs=[output, aux_output])
model.compile(loss=["mse", "mse"], loss_weights=[0.9, 0.1], optimizer="sgd")
history = model.fit(
[X_train_A, X_train_B], [y_train, y_train], epochs=20,
validation_data=([X_valid_A, X_valid_B], [y_valid, y_valid]))
total_loss, main_loss, aux_loss = model.evaluate(
[X_test_A, X_test_B], [y_test, y_test])
y_pred_main, y_pred_aux = model.predict([X_new_A, X_new_B])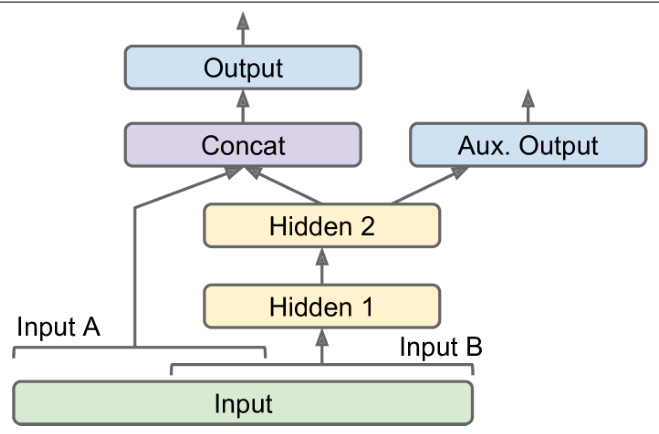
- 每个输出需要它自己的损失函数,并给主输出的损失一个更大的权重
- 训练模型时,也需要为每个输出提供标签
Subclassing API 实现动态模型
Sequential API 和 Functional API 可以推张量形状、检查类型,因为整个模型只是一个静态的层次图
一些模型涉及循环、变化的形状、条件分支和其他动态行为,此时需要 Subclassing API
只需将模型类子类化,在构造函数中创建需要的层,并在
call()方法中执行想要的计算1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class WideAndDeepModel(keras.models.Model):
def __init__(self, units=30, activation="relu", **kwargs):
super().__init__(**kwargs) # handles standard args (e.g., name)
self.hidden1 = keras.layers.Dense(units, activation=activation)
self.hidden2 = keras.layers.Dense(units, activation=activation)
self.main_output = keras.layers.Dense(1)
self.aux_output = keras.layers.Dense(1)
def call(self, inputs):
input_A, input_B = inputs
hidden1 = self.hidden1(input_B)
hidden2 = self.hidden2(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
main_output = self.main_output(concat)
aux_output = self.aux_output(hidden2)
return main_output, aux_output
model = WideAndDeepModel()- 不需要创建输入
- 将构造函数中层的创建与它们在
call()中的使用分开 - 可以在
call()中做任何事 - 模型的架构隐藏在
call(),Keras 不能很好地检查、保存或克隆;调用summary()时,只获得一个层的列表,没有关于它们如何相互连接的任何信息 - 除非真的需要额外的灵活性,否则应该坚持使用 Sequential API 和 Functional API
保存与恢复模型
1 | model.save("my_keras_model.h5") |
- 适用于 Sequential API 和 Functional API
- Subclassing API,使用
save_weights()与load_weights()保存与恢复模型参数,其他内容需要自己保存和恢复
回调
在训练期间定期保存检查点
fit()接受一个回调参数,该参数允许指定一个对象列表;Keras 将在训练开始和结束时、每个 epoch 开始和结束时、甚至在处理每个 batch 之前和之后调用该列表save_best_only设置为 true 时,则会保存在验证集上的性能最好地模型1
2
3
4
5
6
7checkpoint_cb = keras.callbacks.ModelCheckpoint("my_keras_model.h5",
save_best_only=True)
early_stopping_cb = keras.callbacks.EarlyStopping(patience=10,
restore_best_weights=True)
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, early_stopping_cb])自定义(可参见其他文章,如《Python 深度学习》)
1
2
3class PrintValTrainRatioCallback(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
print("\nval/train: {:.2f}".format(logs["val_loss"] / logs["loss"]))
TensorBoard 可视化
将想要可视化的数据输出到称为特殊二进制日志文件——事件文件;每个二进制数据记录称为摘要
TensorBoard 服务器将监控日志目录,自动获取更改并更新可视化
通常,将 TensorBoard 服务器指向一个根日志目录,并配置程序,使其每次运行时都根据时间写入不同的子目录
1
2
3
4
5
6
7root_logdir = os.path.join(os.curdir, "my_logs")
def get_run_logdir():
import time
run_id = time.strftime("run_%Y_%m_%d-%H_%M_%S")
return os.path.join(root_logdir, run_id)
run_logdir = get_run_logdir() # e.g., './my_logs/run_2019_01_16-11_28_43'TensorBoard 的回调
1
2
3
4tensorboard_cb = keras.callbacks.TensorBoard(run_logdir)
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid),
callbacks=[tensorboard_cb])最终得到:
1
2
3
4
5my_logs
├── run_2019_01_16-16_51_02
│ └── events.out.tfevents.1547628669.mycomputer.local.v2
└── run_2019_01_16-16_56_50
└── events.out.tfevents.1547629020.mycomputer.local.v2启动 TensorBoard 服务器(需要预先配置 Path 环境)
1
2$ tensorboard --logdir=./my_logs --port=6006
TensorBoard 2.0.0 at http://mycomputer.local:6006 (Press CTRL+C to quit)
微调超参数
简单地尝试多种超参数组合,看看哪一种在验证集上效果最好(下面为例子)
模型建立
1
2
3
4
5
6
7
8
9
10def build_model(n_hidden=1, n_neurons=30, learning_rate=3e-3, input_shape=[8]):
model = keras.models.Sequential()
options = {"input_shape": input_shape}
for layer in range(n_hidden):
model.add(keras.layers.Dense(n_neurons, activation="relu", **options))
options = {}
model.add(keras.layers.Dense(1, **options))
optimizer = keras.optimizers.SGD(learning_rate)
model.compile(loss="mse", optimizer=optimizer)
return model创建一个
KerasRegressor1
keras_reg = keras.wrappers.scikit_learn.KerasRegressor(build_model)
使用
fit()训练,使用score()方法评估,使用predict()进行预测(score 将与 MSE 相反,前者越高越好);传递给fit()的任何额外参数都将简单地传递给底层的 Keras 模型1
2
3
4
5keras_reg.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])
mse_test = keras_reg.score(X_test, y_test)
y_pred = keras_reg.predict(X_new)
仅关注几种超参数:使用
RandomizedSearchCV,此时使用K倍交叉验证,不使用 X_valid 和 y_valid,后者只是用来 early stop1
2
3
4
5
6
7
8
9
10
11from scipy.stats import reciprocal
from sklearn.model_selection import RandomizedSearchCV
param_distribs = {
"n_hidden": [0, 1, 2, 3],
"n_neurons": np.arange(1, 100),
"learning_rate": reciprocal(3e-4, 3e-2),
}
rnd_search_cv = RandomizedSearchCV(keras_reg, param_distribs, n_iter=10, cv=3)
rnd_search_cv.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])结束时,可以获得最佳参数、最佳分数和训练好的 Keras 模型
1
2
3
4
5rnd_search_cv.best_params_
{'learning_rate': 0.0033625641252688094, 'n_hidden': 2, 'n_neurons': 42}
rnd_search_cv.best_score_
-0.3189529188278931
model = rnd_search_cv.best_estimator_.model其他用于优化超参数的库
- Hyperopt
- Hyperas, kopt 或 Talos
- Scikit-Optimize (skopt)
- Spearmint
- Sklearn-Deap
隐藏层数目
- 深度网络比浅网络具有更高的参数效率
- 可以使用更少的神经元(指数级)来建模复杂函数,从而使它们在相同的训练数据量下达到更好的性能
- 真实世界的数据通常以分层的方式构造——例如,树叶、树枝、树、森林
- 较低的隐藏层对低层结构(例如,各种形状和方向的线段)建模,中间隐藏层组合这些低层结构来对中间层结构(例如,正方形、圆形)建模,而最高的隐藏层和输出层组合这些中间层结构来对高层结构(例如,面)建模
- 利于迁移学习,也常用迁移学习
隐藏层神经元数目
- 通常的做法是将层的大小调整为金字塔形,每层的神经元越来越少——许多低级功能可以合并成更少的高级功能
- 一般来说,增加层数比增加每层神经元的数量更划算
- 选择一个比实际需要的更多层和神经元的模型,然后使用 early stop(或者 dropout 等)来防止过拟合
学习率,batch size等
- 学习率
- 最佳学习速率约为最大学习速率的一半
- 从一个使训练算法发散的大值开始,然后将该值除以 3 并重试
- 训练期间降低学习率
- batch size
- 小批量可以确保每次训练迭代非常快
- 大批量可以给出更精确的梯度估计
- 如果使用 batch normalization,一般不小于20
- 激活函数
- ReLU 适用于所有隐藏层
- 输出层激活看具体需求
- 迭代次数(iterations)
- 早停即可
Training Deep Neural Networks
梯度消失与梯度爆炸
随着算法向下推进到更低的层,梯度通常变得越来越小,梯度下降更新使低层连接权重几乎不变——梯度消失
梯度越来越大,许多层得到大权重更新,算法发散——梯度爆炸
深度神经网络受到不稳定梯度的影响;不同的层可以以不同的速度学习
对于 logistic 激活函数,函数在 0 或 1 时饱和,导数非常接近 0,反向传播开始时,实际上没有梯度通过网络传播回来
为了数据能双向流动,需要每一层输出的方差等于其输入的方差,需要梯度在反向流过一层之前和之后具有相等的方差
每一层必须进行 Xavier initialization(Glorot initialization)

默认情况下,Keras 使用均匀分布的 Glorot initialization。可以通过在创建层时设置
kernel_initializer="he_uniform或kernel_initializer="he_normal "更改为 He initialization
1
2
3
4
5keras.layers.Dense(10, activation="relu", kernel_initializer="he_normal")
# 基于fan_avg
he_avg_init = keras.initializers.VarianceScaling(scale=2., mode='fan_avg',
distribution='uniform')
keras.layers.Dense(10, activation="sigmoid", kernel_initializer=he_avg_init)
非饱和激活函数
ReLU 对正值不饱和,但会导致训练过程中一些神经元死亡——它们只输出 0——尤其是使用了较高的学习率
leaky ReLU 解决此问题:在大型图像数据集上的表现明显优于 ReLU,但在较小的数据集上,有过拟合的风险(Keras 中必须先创建一个实例)
1
2
3leaky_relu = keras.layers.LeakyReLU(alpha=0.2)
layer = keras.layers.Dense(10, activation=leaky_relu,
kernel_initializer="he_normal")ELU:训练时间减少,神经网络在测试集上表现更好,但计算速度比 ReLU 及其变体慢
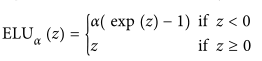
1
2
3# ELU激活函数的一个缩放版本
layer = keras.layers.Dense(10, activation="selu",
kernel_initializer="lecun_normal")
Batch Normalization
以上显著减少训练开始时的梯度消失/爆炸问题

在每个隐藏层的激活函数之前或之后在模型中添加一个操作,简单地对每个输入进行置零和归一化,然后每层使用两个新的参数向量来缩放和移动结果
增加模型的复杂性,预测变慢
Keras 中的 BN 层
1
2
3
4
5
6
7
8
9model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])每个 BN 层每个输入增加4个参数,其中两个参数增加4个参数,不可训练
论文的作者主张在激活函数之前而不是之后添加 BN 层,因此从隐藏层中移除激活功能(BN 层每个输入包含一个偏移参数,因此上一层可以移除偏移项)
1
2
3
4
5
6
7
8
9
10
11model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, kernel_initializer="he_normal", use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("elu"),
keras.layers.Dense(100, kernel_initializer="he_normal", use_bias=False),
keras.layers.Activation("elu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])超参数
axis(默认为 -1):如果想处理 3D 数据(例如[batch size, height, width]),每一个都要归一化,需要设置axis=[1, 2]
梯度裁剪
反向传播过程中简单地裁剪梯度,以防止超过某个阈值
常用于 RNN
Keras 中只需要创建优化器时设置
clipvalue或clipnorm参数1
2optimizer = keras.optimizers.SGD(clipvalue=1.0)
model.compile(loss="mse", optimizer=optimizer)- 把梯度向量的每个分量裁剪为 -1.0 到 1.0 之间——损失的所有偏导数将被限制在此区间
- 可能会改变梯度向量的方向——原始梯度向量为 [0.9,100.0],主要指向第二个轴,但裁剪后得到 [0.9,1.0],大致指向两个轴之间的对角线
- 在实践中,这种方法效果很好
- 要确保渐变裁剪不会改变渐变向量的方向,应该设置
clipnorm而不是clipvalueclipnorm=1.0时,裁剪为 [0.00899964,0.9999595],其方向不变,但几乎消除第一个分量- 容易引起梯度爆炸/消失
复用预训练的层
- 原始模型的输出层通常应该被替换,因为它很可能对新任务一点用都没有
- 原始模型的上层隐藏层不太可能像下层那样有用,因为对新任务最有用的高层特征可能与对原始任务最有用的特征有显著不同
- 首先尝试冻结所有重用的层,然后训练自己模型,看看它如何执行;尝试解冻一两个顶级隐藏层,看看性能是否有所提高
- 如果几乎没有训练数据,尝试删除顶部隐藏层,然后再次冻结所有剩余的隐藏层,迭代,直到找到合适的层数来重用
- 如果有大量的训练数据,可以尝试替换顶部的隐藏层,甚至添加更多的隐藏层
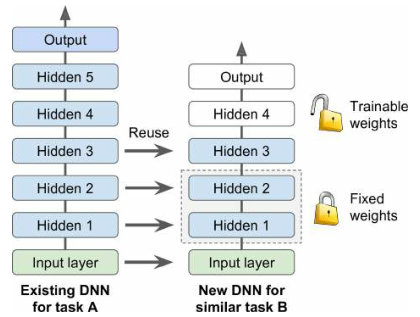
迁移学习
举例:假设 fashion-MNIST 数据集只包含除凉鞋和衬衫之外的8个类别,有人在该集合上构建并训练了一个 Keras 模型 A;现在想训练一个二分类器 B(正=衬衫,负=凉鞋);数据集非常小
加载模型 A,并基于模型 A 创建一个新模型
1
2
3model_A = keras.models.load_model("my_model_A.h5")
model_B_on_A = keras.models.Sequential(model_A.layers[:-1])
model_B_on_A.add(keras.layers.Dense(1, activation="sigmoid"))当训练 model_B_on_A 时,也会影响 model_A,如果想避免这种情况,需要先克隆 model_A
1
2
3# 克隆模型
model_A_clone = keras.models.clone_model(model_A)
model_A_clone.set_weights(model_A.get_weights())冻结层
1
2
3
4for layer in model_B_on_A.layers[:-1]:
layer.trainable = False
model_B_on_A.compile(loss="binary_crossentropy", optimizer="sgd",
metrics=["accuracy"])训练数个 epoch 后,解冻并继续训练(通常需要降低学习率)
1
2
3
4
5
6
7
8
9history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4,
validation_data=(X_valid_B, y_valid_B))
for layer in model_B_on_A.layers[:-1]:
layer.trainable = True
optimizer = keras.optimizers.SGD(lr=1e-4) # the default lr is 1e-3
model_B_on_A.compile(loss="binary_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16,
validation_data=(X_valid_B, y_valid_B))转移学习在小而密集的网络中效果不太好,在深度卷积神经网络中效果最好
无监督预训练
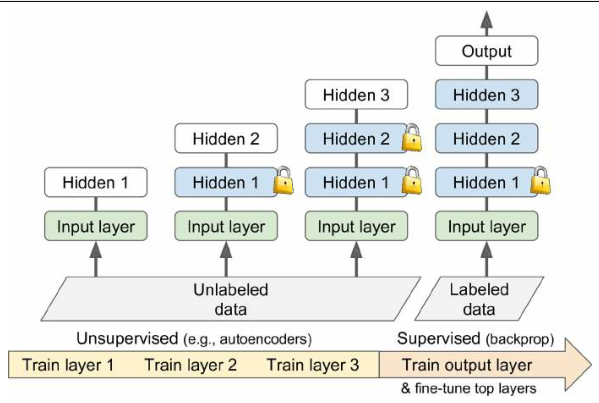
- 场景:处理一个复杂的任务,但没有多少标记的训练数据,也找不到一个为类似任务训练的模型
- 如果可以收集大量未标记的训练数据,可以尝试使用无监督的特征检测器算法,如限制性玻尔兹曼机(RBMs)或自动编码器(现在通常使用后者)
- 每个正在训练的层都是在先前训练的层的输出上训练的
- 一旦所有层都以这种方式进行了训练,就可以为目标任务添加输出层,并使用监督学习(即使用标记的训练示例)来微调最终的网络
辅助任务上预训练
- 场景:没有太多标记的训练数据
- 在辅助任务上训练第一个神经网络,以轻松获得或生成标记的训练数据,然后为实际任务重用该网络的较低层
- 如果想建立一个识别人脸的系统,可能只有每个人的几张照片
- 在网上收集大量随机人物的照片,并训练第一个神经网络来检测两张不同的照片是否表示同一个人
- 重用它的底层将允许你使用很少的训练数据,来训练好的人脸分类器
- 对 NLP,可以下载数百万个文本文档,并从中自动生成标记数据
- 例如,可以随机屏蔽掉一些单词,训练一个模型来预测缺少的单词是什么
- 如果能训练一个模型在这个任务上达到良好的性能,那么它就已经对语言有了相当多的了解,可以在实际任务中复用
更快的优化器
加速训练的方法:
- 对连接权重应用良好的初始化策略
- 使用良好的激活函数
- 使用批处理规范化
- 重用部分预训练网络
- 使用更好的优化器
动量优化
思想:保龄球在光滑的表面上沿着一个缓坡滚下,开始时很慢,但它会很快获得动量,直到它最终达到极限速度
原始的梯度下降不关心早期的梯度是什么,因此如果局部梯度很小,参数更迭会很慢
每次迭代中,动量优化从动量向量 m 中减去局部梯度(乘以学习速率),并通过简单地添加这个动量向量来更新权重

为了模拟某种摩擦机制并防止动量增长过大,该算法引入了一个新的超参数$\beta$,设置在 0(高摩擦)和 1(无摩擦)之间,一般为 0.9
1
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)
缺点在于增加了另一个需要调整的超参数,但经验上取值为 0.9 能获得足够好的效果
Nesterov Accelerated Gradient
对上面方法的优化:计算损失函数的梯度时,不在当前的位置,而是在动量方向的前方

思想:一般来说动量矢量会指向正确的方向(即朝向最佳值),所以使用在那个方向上稍微远一点测量的梯度会比使用在原始位置的梯度稍微精确一些
1
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)
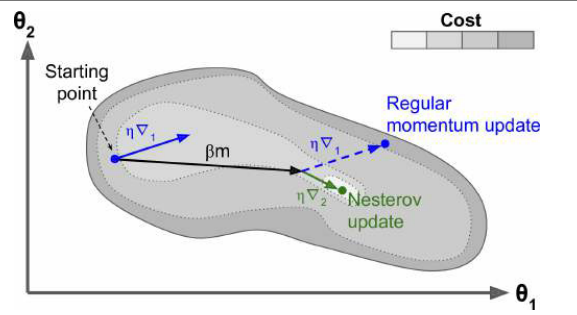
AdaGrad
思想:梯度下降从最陡峭的坡度开始,然后缓慢地沿着谷底下降;算法需要能及早检测到这一点,并纠正其方向,使其更多地指向全局最优
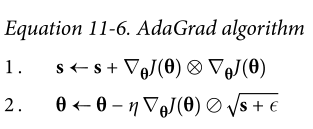
- 梯度的平方累加到向量 s 中(梯度需要逐个元素相乘),如果损失函数沿第 i 维陡峭,则 s 的元素$s_i$将在每次迭代中变得越来越大
- $\epsilon$是一个平滑量,避免除以零
- 按元素除
算法降低了学习速度,但是对于陡峭的维度,学习速度比坡度平缓的维度更快,有助于将结果更新更直接地指向全局最优,并且对学习率的调整更少
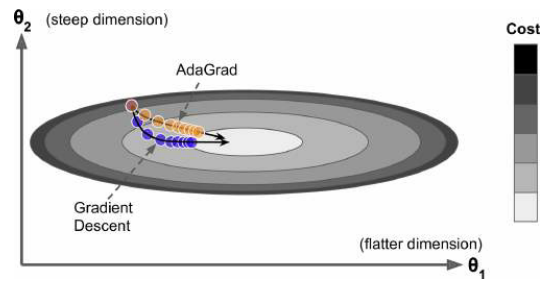
对于简单的二分类问题通常表现良好,但经常早停,因此不适合训练深度神经网络(对于线性回归等更简单的任务可能很有效)
RMSProp
通过仅累加来自最近迭代的梯度(而不是自训练开始以来的所有梯度)来解决 AdaGrad 不会收敛到全局最优值
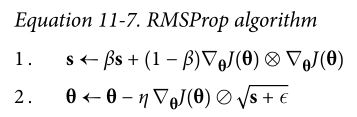
在第一步中使用指数衰减,超参数衰减速率$\beta$通常为 0.9
1
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)
在 Adam 优化出现之前,它一直是首选优化算法
Adam and Nadam Optimization
Adam 结合了动量优化和 RMSProp 的特点
跟踪过去梯度的指数衰减平均值
跟踪过去平方梯度的指数衰减平均值

动量衰减超参数$\beta1$通常为 0.9,标度衰减超参数$\beta2$通常为 0.999,平滑项通常为很小的数$10^{-7}$
1
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
Adam 是一种自适应学习率算法,对学习率超参数的调整要求更少
两种变体
- Adamax
- Nadam optimization
如果性能不好,可以尝试 NAG,数据集可能对自适应梯度“过敏”
学习率调度
从高学习率开始,一旦快速下降停止就降低它
具体策略为:
- Power scheduling
- 学习速率设置为迭代次数 t 的函数 $\eta(t)=\eta_0/(1+t/k)^c$
- 指数 c 通常为 1,k 为超参数,经过 k 此迭代后,学习率下降为初始学习率的一半
- Exponential scheduling
- $\eta(t)=\eta_00.1^{t/s}$
- 每 s 次迭代会下降 10 倍学习率
- Piecewise constant scheduling
- 一些 epoch (5)用较大的学习率,一些 epoch (50)用较小的学习率
- Performance scheduling
- 每 N 次迭代测量一次验证误差
- 当误差停止下降时,学习率降低$\lambda$倍
- Power scheduling
Keras 实现 Power scheduling:只需要设置超参数
decay(k 的倒数),keras 默认指数为 11
optimizer = keras.optimizers.SGD(lr=0.01, decay=1e-4)
Keras 实现 Exponential scheduling:
1
2
3
4
5
6
7
8ef exponential_decay(lr0, s):
def exponential_decay_fn(epoch):
return lr0 * 0.1**(epoch / s)
return exponential_decay_fn
exponential_decay_fn = exponential_decay(lr0=0.01, s=20)
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, [...], callbacks=[lr_scheduler])- LearningRateScheduler 将在 epoch 开始时更新优化器的
learning_rate属性 - 保存模型时,epoch 不会被保存,因此每次调用
fit()都会被重置为 0,因此可以手动设置fit()的initial_epoch参数
- LearningRateScheduler 将在 epoch 开始时更新优化器的
Keras 实现 Piecewise constant scheduling:(如果需要,可以定义一个更通用的函数,并创建一个回调同上)
1
2
3
4
5
6
7ef piecewise_constant_fn(epoch):
if epoch < 5:
return 0.01
elif epoch < 15:
return 0.005
else:
return 0.001Keras 实现 performance scheduling:使用 ReduceLROnPlateau 回调
1
2lr_scheduler = keras.callbacks.ReduceLROnPlateau(factor=0.5, patience=5)
# 只要连续5个epoch内最佳验证损失没有改善,它就会将学习率乘以0.5
通过正则化避免过拟合
已经提过的正则化技术:提前停止,BN
ℓ1 and ℓ2 Regularization
用于约束神经网络的连接权重,而不是 bias
1
2
3
4
5layer = keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
# keras.regularizers.l1() 指定l1
# keras.regularizers.l1_l2() 指定两个值可以使用
functools.partial():它允许为任何可调用的函数创建一个封装,带有一些默认的参数值1
2
3
4
5
6
7
8
9
10
11
12from functools import partial
RegularizedDense = partial(keras.layers.Dense,
activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
RegularizedDense(300),
RegularizedDense(100),
RegularizedDense(10, activation="softmax",
kernel_initializer="glorot_uniform")
])
Dropout
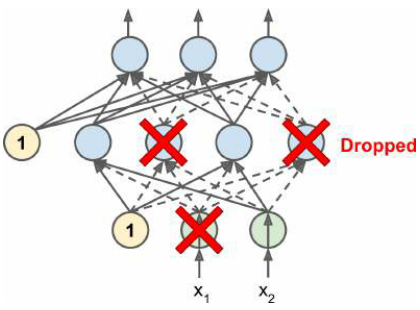
潜在逻辑:不能依靠任何一个神经元来执行任何关键任务;神经元必须学会与许多神经元合作,而不仅仅是少数几个;最终对输入的微小变化不太敏感
Keras 实现
1
2
3
4
5
6
7
8
9model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])如果观察到模型过拟合,可以增加 dropout
会显著降低收敛速度
常规的 dropout 会破坏自正则化(self-normalizing)
Monte-Carlo (MC) Dropout
提供对模型不确定性的度量
实现:
1
2
3
4with keras.backend.learning_phase_scope(1): # force training mode = dropout on
y_probas = np.stack([model.predict(X_test_scaled)
for sample in range(100)])
y_proba = y_probas.mean(axis=0)- 首先强制开启训练模式(通过 with)
- 在测试集预测 100 次后,叠加
- 由于是训练模式,dropout 开启,每次预测都不同。如果测试集为10000个实例且分为10类,则得到数组 [100,10000,10]
- 求平均,得到 [10000,10]——多次预测提供了一个蒙特卡洛估计
预测模式下,可能对一个样本的分类为
[0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.99],但估计下,该样本结果为[0. , 0. , 0. , 0. , 0. , 0.22, 0. , 0.16, 0. , 0.62],说明该样本分类存在不确定性如果模型包含其他层 ,如 BN 层,则不应该强制开启训练模式,而是用 MCDropout 类替换 dropout 层,强制参数
training为真1
2
3class MCDropout(keras.layers.Dropout):
def call(self, inputs):
return super().call(inputs, training=True)
Max-Norm Regularization
对每个神经元,约束引入了权重,使得权重的$l_2$范数不大于一个超参数$r$
不会将正则化损失项添加到总损失函数中
减少$r$会增加正则化的数量,并有助于减少过拟合
Keras 实现:设置每个隐藏层的 kernel_constraint 参数
1
2keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal",
kernel_constraint=keras.constraints.max_norm(1.))可以定义自己的自定义约束函数,并作为参数传入
可以设置
bias_constraint参数来设置 bias 的约束max_norm()有一个默认为0的轴参数,因为密集层通常为 [number of inputs, number of neurons],此时最大范数约束将独立应用于每个神经元的权重向量;对于卷积层,需要设置为axis=[0, 1, 2]
Practical Guidelines

- 模型自正则化——添加 alpha dropout
- 模型不能自正则化——使用 ELU/添加BN/使用max-norm($l_2$)正则化
- 需要一个稀疏的模型——$l_1$正则化
- 运行速度快——不用BN,改为 ReLU
- 风险敏感——使用 MC Dropout 提高性能

