《Deep Learning vs. Traditional Probabilistic Models: Case Study on Short Inputs for Password Guessing》论文阅读记录
摘要
- 与传统的暴力破解攻击和字典攻击相比,密码猜测模型通过泄露的密码库生成猜测密码,期望通过更少的猜测覆盖尽可能多的目标密码
- 本文分析了 8 个泄露密码库的密码模式
password patterns,并对比研究两种主要的概率模型(马尔可夫、PCFG)和 PassGAN(目前最具代表性的深度学习方法)- 对马尔可夫模型应用拉普拉斯平滑
- 对 PCFG 应用语义模式
semantic patterns
- 结果显示:
- 马尔可夫模型可以覆盖大部分测试集的密码
- PassGAN 的表现非常差
- 考虑到攻击者会调整训练集,PCFG 将优于马尔可夫模型
- 暴力攻击与概率模型结合使用时(破解4-8位纯数字口令),original-PCFG 与 modified-PCFG 能分别提高 11% 和 8.5%
介绍
- 文本密码容易使用且对存储空间的需求低。在将来文本密码不太可能被其他的方法【2】替代【1】
- 大多网站使用严格的密码生成策略,以引导用户创建更强的密码。密码强度会实时反馈给用户
- NIST【3】推荐用密码的信息熵
password's information entropy——现代密码攻击下,此方法效果不好【4】 - 密码安全的关键在于密码猜测攻击
- 攻击者创建一个候选密码集
- 攻击者依此一个一个测试,直到猜测密码和目标密码匹配,或者穷尽候选集
- NIST【3】推荐用密码的信息熵
- 暴力攻击:是最基本的策略:在特定的密码空间上尝试所有可能的猜测,直到得到正确的密码空间——不现实,时间和存储空间成本随着密码空间的增加而增加——完全覆盖给定空间需要的猜测次数:$Guess_Number = \sum_{k=i}^n x^k$
- 字典攻击:比前者节省空间。猜测时,攻击者从预定义的字典中逐一尝试可能的密码(构成词典的条目通常被认为是用户更可能用来创建密码的字符串);攻击者可以通过规则集合
mangling-rules,生成更多的猜测 - 一些开创性工作引入了密码猜测概率模型和深度学习模型
- 猜测攻击的有效性很大程度上取决于使用的猜测模型
相关工作
- Weir【5】提出 PCFG,每个密码被分割成字母、数字、特殊符号的子串,并以此生成规则集
- Houshmand【6】向 PCFG 引入了
keyboard mode和multi-word mode - Wang【7】分析了来自中国网站的不同数据集,并系统地调查了中国用户的密码特征。他们在基于 PCFG 的模型中加入了拼音、日期等其他特征;他们一个主要贡献是攻击者能够通过分析数据集的特征,提高覆盖率
- Veras【8】探索密码的语义,他们使用自然语言处理技术来提取对密码中语义模式,并将这些模式添加到基于 PCFG 的模型
- Narayanan【9】首次提出了一种基于马尔可夫模型的猜测模型。他们观察到,容易记住的密码与用户使用的语言具有相似的分布,因此通过低阶马尔可夫链生成密码
- 【10】对马尔可夫模型和 PCFG 模型进行归一化和平滑处理,结果马尔可夫模型比PCFG模型能够覆盖更多的密码
- Hitaj【11】提出了 生成性对抗性网络 PassGAN,不需要手动分析数据集
- Xu【12】将 LSTM 引入密码猜测。在生成密码的下一个字符时,基于LSTM的模型会考虑前缀中的所有字符
数据集分析
数据清洗
收集 8 个密码数据集
删除长度小于 4 或大于 18 的密码
保留仅包含 95 个可打印字符的合法密码
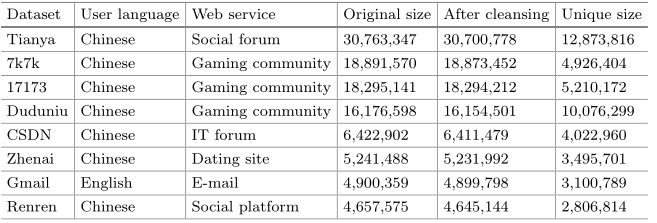
Gmail 为英文库,语言上的差异可能会使数据集在某些方面表现出与其他数据集不同的特征
17173 和 7k7k 在用户语言和网站服务上相同,数据集的大小和唯一的密码分布相当接近——一些特殊的测试中,前者为训练集,后者为测试集;其他六个也可以作为测试集
17173 与 7k7k 的互换是可行的
密码模式
下表显示了密码在每个数据集中的前五位的简单模式(D代表数字序列,L代表字母序列)
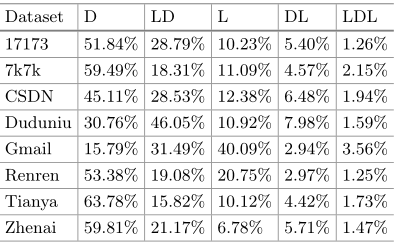
- 数字序列相关的密码模式之和比例较大,中国用户更喜欢数字而不是字母
- Gmail 中纯字母序列占比最高
其他信息
用户喜欢添加自己的生日、姓名等信息
参考【7,8,13,14】,对语义模式分类
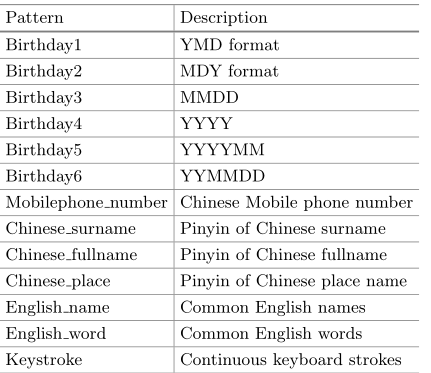
实现数字序列语义模式的正则表达式
汉语语义模式:
- 收集汉语词汇
- 【15】将其转换成汉语拼音
- 从姓氏、中国省市区名收集 568 个条目,分别作为汉语姓氏和汉语地名的汉语词汇
- 从【7】收集 2000 万个预订数据集和三个在线购买数据集(当当,亚马逊中国,凡客诚品)——它们包括买家的姓名——选择这 4 个数据集中的所有中文全名
英文语义模式:
- 根据【8】,英语姓名词典来自【16】,包括自1879年以来美国流行的婴儿姓名。英语单词来自【17】,包括 58110 个小写英语单词【7】
将匹配某个语义模式的密码数除以数据集的大小获得对应比例
- 对于每个密码,确定它们的某个子串是否符合一个语义模式
- 一个密码中的任何子串都不能多次用于形成语义模式:例如 zhangsan,这里子串 zhang 计入姓氏而非全名
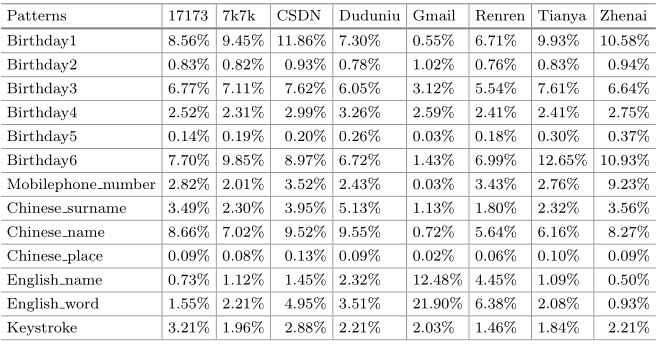
- 结论:
- 出生日期在密码记忆中起着关键作用
- 名字是一组经常使用的语义模式
- 人人网的英文语义模式在中文数据集里最多——基于国内接受英语教育较好的青年学生的用户群体
- 手机号码模式在中文数据集中也有一定的比例
- 连续的键盘字符很容易记住
攻击模型
Original-PCFG
- 将密码分作数字、字母和特殊符号的序列子串
abcd1234的概率计算方式为:$P(abcd1234)=P(L_4D_4)\times P(L_4 \rightarrow abcd)\times P(D_4 \rightarrow 1234)$- $P(L_4D_4)$ 是模板 $L_4D_4$ 在训练集的频率
- $P(L_4 \rightarrow abcd)$ 是
abcd在 $L_4$ 子串集中的出现频率,以此类推
- Weir【5】在密码生成时使用外部字典填充模板中的字母子串
- 模板 $S_1L_3D_3$ 可以转换为前终端结构
pre-terminal structure$!L_3123$ - 之后选择外部字典中长度为 3 的字母序列来代替$L_3$
- PCFG 模型自动地从训练集中导出规则集合
mangling rules,但有效性将取决于外部字典的质量 - 本文还使用训练集中的字母序列来填充模板中的 $L$
- 模板 $S_1L_3D_3$ 可以转换为前终端结构
M-Order Markov Model
- 【9】首次提出马尔可夫模型:一个 m 阶马尔可夫模型对应一个 N-gram(N = m+ 1),下一个字符将由其前 m 个字符决定
- $P(c_1c_2…c_l)=\prod_{i=1}^lP(c_i|c_{i-m}c_{i-m+1}…c_{i-1})$
- 右边的每一项从训练集计算得到:$P(c_i|c_{i-m}c_{i-m+1}…c_{i-1})=\frac{O(c_{i-m}c_{i-m+1}…c_{i-1}c_i)}{\sum_{c\in\sum}O(c_{i-m}c_{i-m+1}…c_{i-1}c)}$
- 分子为出现次数,分母中的 $\sum$ 表示包含 95 个可打印字符的字典
- 在第一个字符前添加填充符号,并在末尾添加特殊的结束符号
- 阶数过高,则很多概率为0,因此【10】引入了平滑技术,解决数据稀疏问题,本文和【10】添加拉普拉斯平滑,分子分母都增加一个常数 $\delta=0.01$(分母最终增加 $\delta \times \sum$)(字符集大小为 96)
- 右边的每一项从训练集计算得到:$P(c_i|c_{i-m}c_{i-m+1}…c_{i-1})=\frac{O(c_{i-m}c_{i-m+1}…c_{i-1}c_i)}{\sum_{c\in\sum}O(c_{i-m}c_{i-m+1}…c_{i-1}c)}$
- 【10】将生成密码的过程建模为搜索树,父节点为 $c_1c_2…c_{l-1}$ 和子节点 $c_1c_2…c_l$ 之间的连接用转移概率标记;树中的节点存储在优先级队列中,按概率降序排列,每次迭代时,概率最高的节点出列,更多的子节点被推入优先级队列。如果出列节点的最后一个字符是终结字符,则对应于该节点的字符串是密码猜测
- 本文输出猜测密码以及它们的概率,在生成所有高于给定概率阈值的密码后,根据概率间隔将它们分成块,并对每个块的密码进行排序
PassGAN
- 【11】提出 PassGAN
- 利用生成对抗网络,可以自动从训练集中获取密码的分布;遗传神经网络由生成深层神经网络 G (生成器)和判别深层神经网络 D(鉴别器)组成。每次迭代都会给它一个输入 I,生成器 G 生成一个伪样本,鉴别器 D 的目标是区分生成的来自 G 的样本和来自 I 的真实样本,当 D 无法区分 G 生成的伪样本和真实样本时,认为训练完成
- IWGAN 要求输入字符串的长度一致,因此使用填充符号扩展训练集中的密码长度
- 参数遵循【11】,下图显示不同 checkpoint 下分别生成 500w 密码猜测的覆盖率(训练集为 17173,测试集为 7k7k)
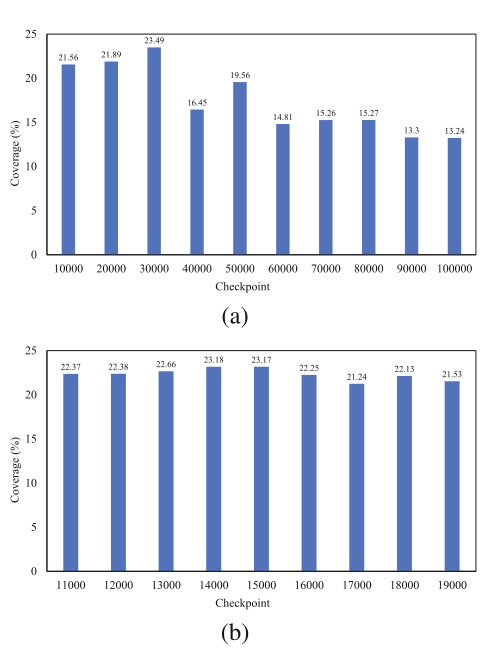
Modified-PCFG
Original-PCFG 将密码字符串分割成三种类型的子字符串,但用户选择的密码往往有语义
Modified-PCFG 模型的分割首先确定子串是数字序列还是字母序列,然后确定它们是否符合某种语义模式的定义。不符合的子串仍定义为 $D_n$ 与 $L_n$
具体算法如下:

执行结果
Markov vs PCFG
马尔可夫的概率阈值设置为 $10^{-10}$,训练 1-5 元,添加拉普拉斯平滑,训练集为 17173
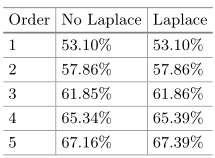
猜测次数-覆盖率图表说明
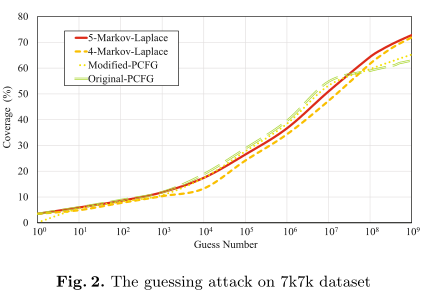
选择了两个性能最好的模型——5-拉普拉斯和4-拉普拉斯——与 Original-PCFG 和 Modified-PCFG 对比,猜测次数设为10亿
探索了训练集大小的影响:模型在使用完整的训练集时可以学习完整的密码分发信息,但这种优势只有在猜测数达到一定数量时才能体现出来
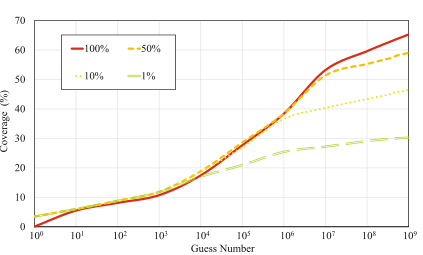
PassGAN vs 概率模型
生成不重复的密码
PassGAN 效果最差,但不需要任何的密码先验知识
其他测试结果
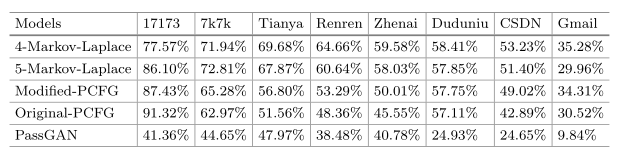
语言上的差异使得训练集和测试集有不同的分布
训练集与测试集相同(对训练集进行猜测攻击):
出发点是攻击者可以根据被攻击数据集的特征调整自己的训练集
极端的情况:攻击者得到一个与测试集几乎没有区别的训练集
PassGAN 仍然无法达到预期的效果:PassGAN适合在数据集内训练高频长度的密码,如【11】
把17173数据集中长度为4到9的密码拿出来,把每个长度的所有密码分别输入 PassGAN 模型中进行训练
结果如下
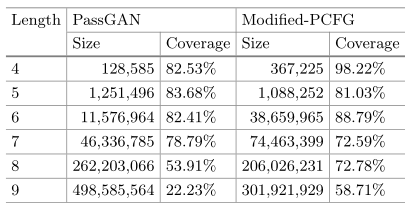
联合攻击
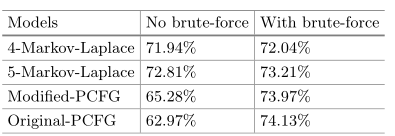
暴力攻击和概率模型组合,共同破解长度 4-8 的纯数字密码
此时应当生成 111,110,000 条密码(纯数字),再用概率模型生成概率最高的 88,890,000 条密码,二者混合后测试覆盖率
参考文献
- Zhu, B., Yan, J., Bao, G., Yang, M., Xu, N.: Captcha as graphical passwords- a new security primitive based on hard AI problems. IEEE Trans. Inf. Forensics Secur. 9, 234–240 (2014)
- van Herley, C., Oorschot, P.: A research agenda acknowledging the persistence of passwords. IEEE Secur. Priv. 10, 28–36 (2012)
- Burr, W.E., et al.: NIST SP800-63-2: Electronic authentication guideline. National Institute of Standards and Technology, Reston, V A, Technical report, Special Publication (NIST SP) - 800–63-1 (2011)
- Matt, W., Sudhir, A., et al.: Testing metrics for password creation policies by attacking large sets of revealed passwords. In: ACM CCS 2010, pp. 162–175 (2010)
- Matt, W., Sudhir, A., et al.: Password cracking using probabilistic context-free grammars. In: IEEE Symposium on Security and Privacy, pp. 391–405 (2009)
- Houshmand, S., Aggarwal, S., Flood, R.: Next gen PCFG password cracking. IEEE Trans. Inf. Forensics Secur. 10, 1776–1791 (2015)
- Wang, D., Cheng, H., et al.: Understanding Passwords of Chinese Users: Characteristics, Security and Implications, July 2014. https://www.researchgate.net/profile/Ding_Wang12/publication/269101022_Understanding_Passwords_of_Chinese_Users_Characteristics_Security_and_Implications/links/5544e2700cf23ff7168696a8.pdf
- Veras, R., Collins, C., Thorpe, J.: On the semantic patterns of passwords and their security impact. In: Network and Distributed System Security Symposium (2014)
- Arvind, N., Vitaly, S.: Fast dictionary attacks on passwords using time-space trade-off. In: ACM CCS 2005, pp. 364–372 (2005)
- Ma, J., Yang, W., Luo, M., Li, N.: A study of probabilistic password models. In: Proceedings of IEEE Symposium on Security and Privacy, pp. 689–704 (2014)
- Hitaj, B., Gasti, P., Ateniese, G., Pérez-Cruz, F.: PassGAN: a deep learning approach for password guessing. CoRR abs/1709.00440 (2017)
- Xu, L., Ge, C., et al.: Password guessing based on LSTM recurrent neural networks. In: IEEE International Conference on Computational Science and Engineering, pp. 785–788 (2017)
- Li, Y., Wang, H., Sun, K.: A study of personal information in human-chosen passwords and its security implications. In: IEEE INFOCOM, pp. 1-9 (2016)
- Wang, D., Zhang, Z., Wang, P., Yan, J., Huang, X.: An underestimated threat. In: ACM CCS, Targeted Online Password Guessing (2016)
- ChineseTone. https://github.com/letiantian/ChineseTone
- ssa.gov. https://www.ssa.gov/oact/babynames/limits.html
- English words. http://www.mieliestronk.com/wordlist.html
- Gulrajani, I., Ahmed, F., et al.: Improved Training of Wasserstein GANs. CoRRabs/1704.00028 (2017). http://arxiv.org/abs/1704.00028

