More Than Code

Password Guessing Based on LSTM Recurrent Neural Networks

发表于 分类于
本文字数： 4.8k 阅读时长 ≈ 4 分钟

《Password Guessing Based on LSTM Recurrent Neural Networks》论文阅读笔记

摘要

  • 人们倾向于选择有意义的单词或数字作为密码，许多密码很容易猜测
  • 介绍了一种基于 LSTM 的密码猜测方法
  • 在用 Rockyou 数据集的 3000 万个密码训练 LSTM 神经网络之后，生成 33.5 亿个密码可以覆盖剩余 Rockyou 数据集的 81.52%。与 PCFG 方法和马尔可夫方法相比，该方法具有更高的覆盖率

介绍

  • 密码猜测旨在生成密码字典或数据集，以最小的大小覆盖尽可能多的用户密码
    • 生成的密码可以检测用户密码的安全风险
    • 生成的密码可以提升字典攻击的性能
  • 近年的密码生成研究：
    • 使用更好的模板【1，5，7，13，14】
    • 使用字符之间的相互关系——马尔可夫模型【2，8，10】
  • 递归神经网络具有揭示密码中所有字符之间相互关系的能力，而基于马尔可夫的模型仅考虑几个相邻字符之间关系
  • 本文用泄露的密码训练网络，用搜索算法生成密码
    • 实现了基于 LSTM 神经网络的密码猜测
    • 对不同层数/神经元进行了比较

相关工作

  • PCFG：
    • Weir【1】提出 PCFG，从训练密码生成模板并用字典填充模板用于密码猜测
    • Chou【7】开发了 TDT 模型来生成更精确的模板和字典
    • Li 【5】改进了 PCFG，增加了中文拼音和规则
    • Veras【14】用语义和句法标签建立 PCFG
    • Houshmand【13】等人用键盘模式keyboard patterns和多字模式multiword patterns优化了猜测效率【13】
  • Markov
    • Narayanan【10】在字典攻击中首次引入马尔可夫模型
    • Castelluccia【2】将马尔可夫模型用于密码强度衡量
    • Dürmuth【8】实现基于马尔可夫模型的的密码破解工具 OMEN，通过生成 100 亿个密码，猜中了 260 万个 Rockyou 密码的80%以上
  • JTR【11】 与 Hashcat【3】
    • 被用于有针对性的在线密码猜测【12】
    • 【4、6】侧重于这两个模型的组合与评估
    • 【4】显示，基于马尔可夫的模型比基于模板的模型显示出更好的结果
  • Melicher【15】提出神经网络用于密码强度测量，使用 PGS 和 PGS+ 数据集训练数据，并用 MTurk 和 000Webhost 数据集测试

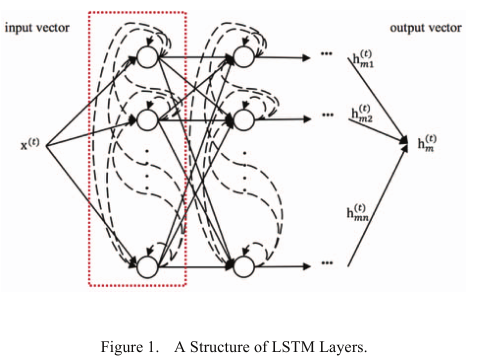
LSTM 循环神经网络

  • 递归神经网络能够从序列中学习

  • 递归神经网络中的神经元用长短期记忆（LSTM）神经元代替【9】，以避免梯度消失问题

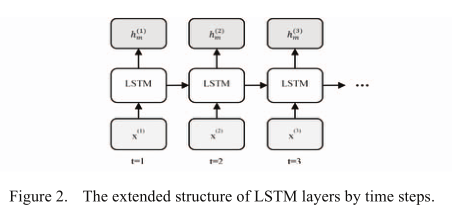
  • LSTM 层的外部输入是一个数据向量矩阵，矩阵的行长度代表序列的长度，等于时间步长的数量。矩阵的列长表示批次中的序列数（批次大小）；在每个时间步长，LSTM 层的外部输入是矩阵的列向量；一层的输出向量在下一个时间步会反馈给同一层的神经元

    image-20210221162407761

    image-20210221162515540

softmax 回归

  • Softmax 回归为多分类问题设计【16】

  • 标签（类别）组成子集 C，标签个数为|C|

  • 分类概率可以估计（$y$ 代表标签，$\theta$ 代表回归的参数）：

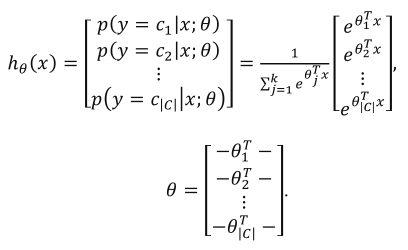
    image-20210221162719730

实现

密码猜测模型

  • 本文神经网络包括一个输入层，几个 LSTM 层，一个 softmax 层和一个输出层
  • 基本的假设：
    • 密码 $p_1p_2…p_{len}$ 是一个序列 $x(1)=p_1,x(x)=p_2,…,x(len)=p_{len}$
    • $x(t)$ 与前面的所有字符相关
  • 基本的思路：
    • $x(t)$ 的分布可以通过向网络输入 $x(1), x(2),…,x(t-1)$ 获得
    • 泄露密码集训练网络
    • 训练后给定前缀，下一个字符可以根据概率分布，由选择算法来决定
    • 密码中的每个字符（除了第一个字符）可以根据顺序预测

密码预处理

  • 泄露的密码分为3个部分：训练集、验证集（防止过拟合）和测试集
  • 预处理：
    • 数据清洗
      • 确定密码的字符字典（添加特殊终止字符），以及密码长度范围
      • 删除包含不良字符的密码
      • 删除超过限制长度的密码
      • 打乱密码
    • 数据格式转换
      • 密码字符替换
      • 序列变换：将 $L(p_1)L(p_2)…L(p_{len})$ 转换为 $x^{(1)}=L(p_1),x^{(2)}=L(p_2),…,x^{(len)}=L(p_{len}),x^{(len+1)}=L(END)$

训练

  • 给定训练数据 $x^{(1)}=L(p_1),x^{(2)}=L(p_2),…,x^{(len)}=L(p_{len}),x^{(len+1)}=L(END)$，监督的标签为 $y^{(1)}=x^{(2)},y^{(2)}=x^{(3)},…, y^{(len)}=x^{(len+1)}=L(END)$
  • 这里介绍了训练的原理（略）

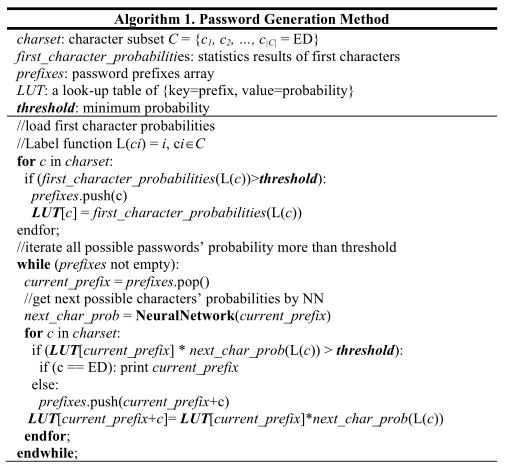
密码生成

  • 由于能够预测字符的概率分布，每个密码前缀出现的可能性可以通过概率乘法公式来估计

    image-20210221165456608

测试指标

  • 覆盖率

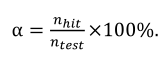
    image-20210221165730503

实验结果

RNN 的重要参数

Hidden Layers Number (HLN)

  • 实现了三个具有不同数量 LSTM 隐藏层（1、2、3层）的网络

  • 实验在小规模生成数据集上进行，密码生成阈值为 $10^{-6}、10^{-7}、10^{-8}、10^{-9}$

  • 下图为结果。x 轴代表生成密码数目的对数；HLN 的增加给结果带来轻微的、不明显的增加(在相同的阈值下仅约1%)

    image-20210221170033895

Neurons Number per Layer (NNPL)

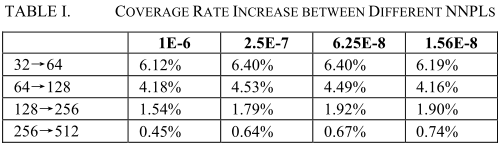
  • 实现了五个两层的 LSTM 网络，每层神经元数目分别为32，64，128，256，512

  • 实验在小规模生成数据集中进行，阈值同上

  • 下图为结果

    • 随着 NNPL 的增加，覆盖率增加

    • 覆盖率的增加逐渐减少

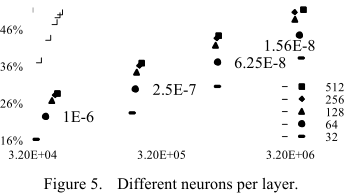
      image-20210221170354340

  • 随着 HLN 和 NNPL 的增加，覆盖率在相同的阈值下增加，但训练和生成速度降低

    • 后面的实验，选择了具有 2 个隐藏 LSTM 层、每个 LSTM 层有 256 个神经元的 RNN

      image-20210221170544776

与过往研究的对比

  • 采样一些大规模数据集，与过去的研究对比

  • LSTM 模型包含 2 个隐藏的 LSTM 层，每层有 256 个神经元，由 3000 万个 Rockyou（RY）密码训练，包括 2700 万的训练集和 300 万的验证集

  • 测试集：Rockyou 260万密码；Myspace 密码；Facebook 密码

  • 与 OMEN-4Gram、概率上下文无关语法（PCFG）、JtR 马尔可夫模式和 JtR 增量模式JtR incremental mode进行比较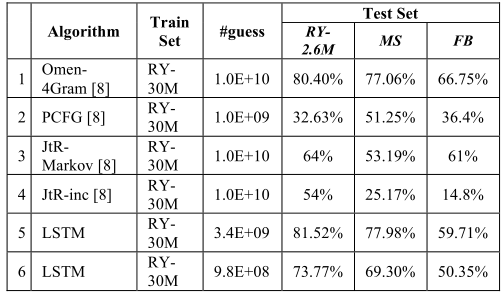

    image-20210221163301563

结论

  • LSTM 递归神经网络可以应用于密码猜测
  • 神经网络优于基于模板和基于马尔可夫的模型
  • 了获得更好的结果，可以进一步调整神经网络的结构
  • 未来的工作可能侧重于不同数据集之间的差异，研究常见或特定的神经网络

参考文献

[1] M. Weir, S. Aggarwal, B. d. Medeiros and B. Glodek, “Password Cracking Using Probabilistic Context-Free Grammars,” in 30th IEEE Symposium on Security and Privacy, 2009, pp. 391-405.

[2] C. Castelluccia, M. Dürmuth and D. Perito, “Adaptive Password Strength Meters from Markov Models,” in NDSS, 2012.

[3] J. Steube, “hashcat - advanced password recovery,” [Online]. Available: www.hashcat.net.

[4] J. Ma, W. Yang, M. Luo and N. Li, “A study of probabilistic password models,” in 2014 IEEE Symposium on Security and Privacy, 2014, pp. 689-704.

[5] Z. Li, W. Han and W. Xu, “A large-scale empirical analysis of chinese web passwords,” in 23rd USENIX Security Symposium, 2014, pp. 559-574.

[6] B. Ur, S. M. Segreti, L. Bauer, N. Christin, L. F. Cranor, S. Komanduri and R. Shay, “Measuring real-world accuracies and biases in modeling password guessability,” in 24th USENIX Security Symposium, 2015, pp. 463-481.

[7] H. C. Chou, H. C. Lee, H. J. Yu, F. P. Lai, K. H. Huang and C. W. Hsueh, “Password cracking based on learned patterns from disclosed passwords,” International Journal of Innovative Computing, Information and Control, vol. 9, Feb. 2013, pp. 821-839.

[8] M. Dürmuth, F. Angelstorf, C. Castelluccia, D. Perito and A. Chaabane, “OMEN: Faster password guessing using an ordered markov enumerator,” in International Symposium on Engineering Secure Software and Systems, 2015, pp. 119-132.

[9] Z. C. Lipton, J. Berkowitz and C. Elkan, “A critical review of recurrent neural networks for sequence learning,”. Available: arxiv.org/pdf/1506.00019.pdf.

[10] A. Narayanan and V. Shmatikov, “Fast dictionary attacks on passwords using time-space tradeoff,” in Proceedings of the 12th ACM conference on Computer and communications security, 2005, pp. 364-372

[11] S. Designer, “John the Ripper password cracker,” [Online]. Available: www.openwall.com/john.

[12] D. Wang, Z. Zhang, P. Wang, J. Yan and X. Huang, “Targeted online password guessing: An underestimated threat,” in Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, 2016, pp. 1242-1254.

[13] S. Houshmand, S. Aggarwal and R. Flood, “Next gen PCFG password cracking,” IEEE Transactions on Information Forensics and Security, vol 10, Aug. 2015, pp. 1776-1791.

[14] R. Veras, C. Collins and J. Thorpe, “On Semantic Patterns of Passwords and their Security Impact,” in NDSS, 2014.

[15] W. Melicher, B. Ur, S. M. Segreti, S. Komanduri, L. Bauer, N. Christin, and L. F. Cranor, “Fast, lean and accurate: Modeling password guessability using neural network,” in Proceedings of USENIX Security, 2016.

[16] Stanford UFLDL. “Softmax Regression” [Online]. Available: http://ufldl.stanford.edu/wiki/index.php/Softmax_Regression.

相关文章推荐