More Than Code

A Study of Probabilistic Password Models

发表于 分类于
本文字数： 10k 阅读时长 ≈ 9 分钟

《A Study of Probabilistic Password Models》论文阅读记录

摘要

  • 概率密码模型为每个字符串分配一个概率值
  • 由密码模型生成的猜测数图是密码研究中广泛使用的方法。本文证明了概率阈值图比猜测数图具有重要的优势——计算速度要快得多，提供的信息也超出了猜测数字图的范围
  • 对大量概率密码模型进行了系统评估，包括使用不同归一化和平滑方法的马尔可夫模型
  • 马尔可夫模型在正确使用时性能明显优于 Weir【25】 提出的 PCFG 模型

介绍

  • 密码既易于理解和使用，又易于实施——基于密码的身份验证可能会继续作为安全的重要组成部分【14】
  • 密码模型分为两类，全字符串模型和基于模板的模型
    • 全字符串模型不将密码分成段，如【8】中的马尔可夫模型
    • 基于模板的模型通常将将密码分成几个部分，同一类别的连续字符分成一个片段，独立地为每个片段生成概率，如【21】，【25】
  • 认为密码模型研究分两类
    • 第一类研究旨在了解是什么让用户选择更安全的密码——密码模型比较这些密码集的相对强度
      • 【17】、【18】、【22】、【23】、【26】研究了不同场景下用户密码选择的质量
      • 用特别方法估计一组密码的信息熵【7】，主要基于密码长度
      • 【25】开发 PCFG
      • 往往绘制猜测数字图——需要计算密码的猜测数，这在计算上是昂贵的，而且往往只能探索一部分搜索空间
    • 第二类研究旨在寻找最佳密码模型——模型用于评估所选密码的安全级别
  • 本文认为
    • 对于第一类研究，比较两组密码的相对强度没有必要计算所有密码的猜测数，只需计算所有密码的概率，绘制概率阈值与密码破解百分比的曲线
      • 计算速度快
      • 曲线显示了集合中的密码质量
    • 以往的工作只考虑了非常简单的马尔可夫模型
      • 许多平滑技术可以帮助解决高阶马尔可夫模型中的稀疏和过拟合问题，包括拉普拉斯平滑、古德图灵平滑【13】和回退【16】
      • 密码具有非常确定的长度分布，但 n-gram 最后分配给所有固定长度字符串的概率加起来为1，隐含地假设了长度分布是均匀的
      • 不同的密码建模方法尚未得到系统的评估或相互比较
    • 本文对比了 3 个英文数据库，3 个中文数据库
    • PCFG 使用了三种字典：【25】的字典、OpenWall 字典、训练集生成的字典
    • 马尔可夫使用三种规范化：长度均匀分布、基于训练集长度分布、基于结束符号
    • 高阶马尔可夫链表现出不同程度的过拟合——在破解高概率密码方面表现良好
    • backoff 方法本质上是可变阶马尔可夫链，与基于结束符号的规范化结合，效果最好
  • 本文贡献
    • 介绍了概率阈值图进行密码研究
    • 从 n-gram 模型的丰富文献中引入知识和技术到密码建模中
    • 对许多密码模型进行了系统的评估并取得了一些发现

相关工作

  • 一个活跃的研究领域是研究不同场景下用户密码选择的质量
    • 面对不同的密码策略【18】、【17】
    • 面对不同的密码强度计【23】、【10】
    • 由于到期而被迫改变密码【26】
    • 在密码中加入额外随机性【12】
  • 早期的工作
    • 使用了标准密码破解工具的组合 JTR【3】
    • 估计一组密码信息熵——主要基于密码长度【7】，即 $log_2((alpha.size)^{len})$ ——【22】使用了更复杂的方式，即在计算熵的时候考虑数字、大写字母、特殊符号出现的次数和位置
  • Weir 等人开发了 PCFG【25】并认为熵估计的方法是错误的【24】，并且建议使用猜测的密码数。此模型和其他变体成为了密码研究的标准方法【17】、【18】、【15】、【23】、【20】
  • JTR【3】是最流行的密码破解工具之一，有几种模式：
    • 单词列表模式使用字典和各种管理规则
    • 增量模式使用三字符（trigraph）频率：字符、位置和密码长度三元组的频率
    • 马尔可夫模式使用一阶马尔可夫链
  • Castelluccia 等【8】提出使用全串马尔可夫模型来评估密码强度
  • 【9】通过计算数据集中每个密码的估计概率，并使用近似算法计算每个阈值的猜测次数，比较马尔可夫模型在多个数据集上的破解效率，但没有考虑归一化和平滑的问题
  • 【19】研究了密码分布与 Zipf 分布的匹配程度，他们将 RockYou 数据集拟合为 ZIPF 分布 $\frac{1}{r^b},b=0.7878$，但只适用于猜测数目在 $2^6$ 到 $2^20$ 之间的密码

密码模型与指标

  • 设置字符集 $\Sigma$ 为 95 个可打印的 ASCII 字符，子集称为字符类别，密码长度为 4-40
  • 使用以下三种指标：
    • 对于类型一的研究，模型对比不同的数据集
    • 对于类型二的研究，固定一个数据集，对比不同的模型

Guess-number graphs

  • 以对数标度绘制猜测次数与数据集中破解密码的百分比

Probability-threshold graphs

  • 以对数标度绘制了概率阈值与高于阈值的密码百分比

  • 只需计算模型分配给测试数据集中每个密码的概率；对于每个概率阈值，计算有多少密码被赋予了高于阈值的概率

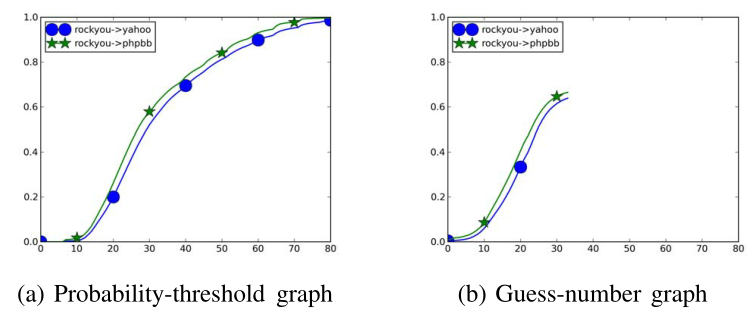
    image-20210226133632274

  • 二者的对应关系：

    • 第一类研究：
      • 两条猜测数曲线的关系与相应概率阈值曲线的开始部分所展示的完全相同，因为对于给定的阈值，将尝试完全相同的密码集
      • 唯一缺少的信息是不知道每个概率阈值对应的确切猜测数，但无关紧要
    • 第二类研究：
      • 当比较两个密码模型时，从概率阈值图中得出的结论是否可以结转到猜测数图取决于这两个模型是否具有相似的密码排名，如果已知两个密码模型产生非常相似的排名分布，那么从概率-阈值图得出的任何结论也将适用于猜测数图，因为相同的概率阈值将对应于相同的猜测数

  • 在第二类研究中使用概率阈值图有限制

Average-Negative-Log-Likelihood ($ANLL$) and $ANLL_\theta$

  • 概率阈值曲线中的信息可以用一个测量曲线左侧面积的数字概括，这个数字与平均负对数似然（$ANLL$）完全相同
    • 以行微分该区域，得到一行的长度为 $y<-log_2p<y+dy$，求和
  • $ANLL_\theta$：定义为 $\theta$ 以下曲线左侧的面积，因为 $ANLL$ 包括 100% 破解密码的信息，但生成足够的猜测来破解最难的密码可能是不可行的
  • $ANLL(D|P) = \frac{1}{|D|}\sum_{s \in D}-log_2p(s)$，其中 $D$ 为测试密码集，$s$ 为测试集中可重复出现的密码，$p$ 为数据集给出的概率分布

密码模型设计

  • 主要考虑在不依赖外部字典的情况下构建密码模型的方法，依赖外部字典的方法的性能在很大程度上取决于字典的质量，特别是字典与测试数据集的匹配程度

Whole-String Markov Models

  • JTR【3】的马尔可夫模式和【8】用了 Whole-String Markov Model
    • JTR：一阶 $P(c_1c_2…c_l)=P(c_1)P(c_2|c_1)…P(c_l|c_{l-1})$，$P(c_i|c_{i-1})=\frac{count(c_{i-1}c_i)}{count(c_{i-1} \cdot)}$
  • 在每个密码前面加上开始符号

正则化

  • 【3】、【8】模型不是概率模型，所有的概率之和为 最大密码长度-最小密码长度+1（分配给固定长度的所有字符串概率之和为1）证明（当阶数为 1 时）：

    • $\sum_{c_1 \in \Sigma}P(“c_1”)= \frac{\sum_{c_1\in\Sigma}count(c_0c_1)}{count(c_0\cdot)}=1$ 因此所有 length-1 字符串的概率和为 1

    • 假设所有 length-l 字符串的概率和也为 1，则对于 length-(l+1) 的字符串概率和：
      $$
      \sum_{c_1c_2…c_{l+1}\in\Sigma^{l+1}}P(“c_1c_2…c_{l+1}”) \ = \sum_{c_1c_2…c_l\in\Sigma^l}P(“c_1c_2…c_l”) \times \sum_{c_{l+1}\in\Sigma}P(c_{l+1}|c_l) \ = \sum_{c_1c_2…c_l\in\Sigma^l}P(“c_1c_2…c_l”) =1
      $$

    • 阶数为 n 的时候同理

    • 需要归一化

  • Direct normalization：每个概率除以（最大密码长度-最小密码长度+1）；此时假设每个长度的密码的总概率是相同的，但和下面的表不符

  • Distribution-based normalization：基于不同长度密码的分布标准化，即对于每个长度为 m 密码对应概率乘 $\frac{passwords\ of\ length\ m \ in \ training}{total\ passwords\ in\ training}$；可能导致过拟合，训练和测试数据集可能具有不同的长度分布

  • End-symbol normalization：在训练和测试中在每个密码附加一个结束符号，则 $P(c_1|c_0)P(c_2|c_1)…P(c_l|c_{l-1})P(c_e|c_l)$，对最大长度密码，定义 $P(c_e|c_U)=1$；此方法考虑了哪些子字符串更有可能出现在密码的末尾，前面的方法中 “passwor” 将分配到比 “password” 更高的概率；且保证了，当阶数大于等于最小密码长度 L 时，分配给所有字符串的概率之和为 1

  • 马尔可夫链阶数、平滑方法

    • 高阶马尔可夫链能够使用比低阶马尔可夫链更深的历史信息，但容易过拟合，且存在稀疏性问题——从非常小的计数结果计算转移概率，或者许多字符串被指定概率为 0
    • 拉普拉斯平滑：将 $\delta$ 加到每个子字符串的计数结果上
    • Good-Turing 平滑【13】

  • Backoff【16】：同时解决顺序、平滑和稀疏性问题的另一种方法是使用可变阶马尔可夫链

    • 选择一个阈值并存储计数超过阈值的所有子字符串
    • 令 $\pi_{i,j}$ 表示 $s_0s_1…s_l$ 中从 $s_i$ 到 $s_j$ 的子串
      • 计算 $s_0s_1…s_{l-1}$ 到 $s_0s_1…s_l$ 的转移概率时，寻找最小的 $i$ 使得 $\pi_{i,l-1}$ 有超过阈值的计数
      • 当有计数时，直接得到 $\frac{count(\pi_{i,l})}{count(\pi_{i,l-1})}$
      • 当 $\pi_{i,j}$ 没有计数，则只能靠较短的历史分配概率
        • 计算通过第一种情况将转移概率分配给所有字符后留下的概率 $b$
        • 使用更短的前缀 $\pi_{i+1,l-1}$ 计算所有其他字符的概率，归一化使其相加为 $b$
    • backoff 模型比其他马尔可夫模型要慢得多

Template-based Models

  • 根据字符的类别将密码划分为不同的模板，并计算模板对应的字段概率：$P(“passwd123”)=P(“\alpha^6\beta^3”)P(“passwd”|\alpha^6)P(“123”|\beta^3)$

  • 模板概率

    • 分配给每个模板的概率仅仅是使用该模板的密码数量除以密码总数——使用未出现在训练数据集中的模板的密码概率为 0
    • 改良：
      • 将密码根据（小写字母、数字、大写字母、符号）分割为字段
      • 学习马尔可夫模型，利用马尔可夫模型将概率分配给模板

  • 字段概率：“123”的概率是“123”作为训练数据集中的 3 位片段出现的次数除以训练数据集中的 3 位片段的数量，或通过马尔可夫模型生成概率

    image-20210226192320553

Password Generation

  • 基于全串马尔可夫：
    • 搜索空间建模为一棵搜索树
    • 优先级队列方法不是存储器效率高的，并且不能用于生成大量密码
    • 优化：阈值搜索（不适用于基于模板的模型）
      • 对搜索树进行多次深度优先遍历：第 i 次迭代，通过深度优先遍历搜索树，对概率小于 $\rho_i$ 的所有节点剪枝，生成概率在 $(\rho_i,\tau_i)$ 之间的密码
      • 为了生成 n 个猜测密码，从 $(\rho_1=\frac{1}{n},\tau_1=1)$ 开始迭代，若第 i 次迭代后共生成 m 个密码，则 $(\rho_{i+1}=\frac{\rho_i}{max(2, 1.5n/m)},\tau_{i+1}=\rho_i)$
  • 本文中，除了PCFGW模型之外，不为基于模板的模型生成密码（阈值搜索不适用于基于模板的模型）

实验方法

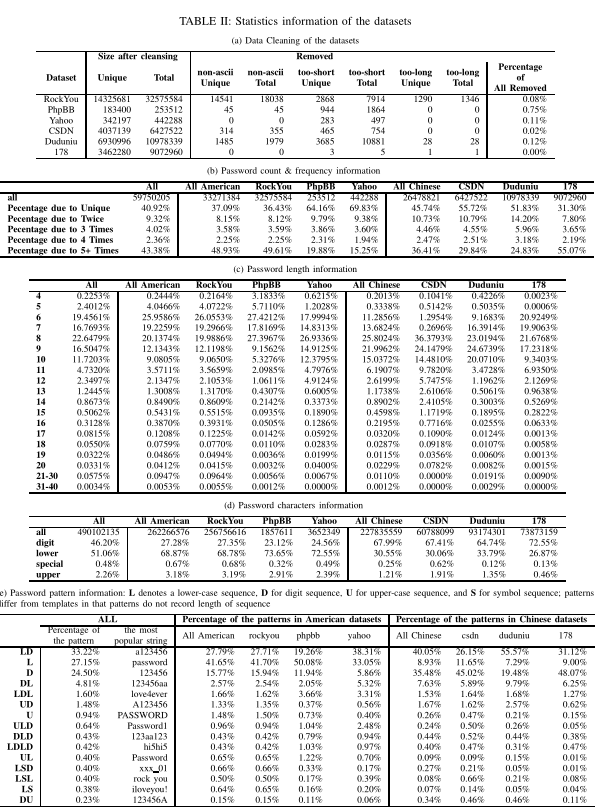
数据集

  • RockYou【1】包含2009年12月从社交应用网站 Rockyou 泄露的 3200 多万个密码
  • PhpBB【1】包括布兰登·恩莱特在2009年1月从 PhpBB 泄露的 MD5 散列中破解的大约 25 万个密码
  • Yahoo 数据集包括名为 D33Ds 的黑客组织在 2012 年 7 月公布的大约 45 万个密码
  • CSDN 数据集包括中国软件开发商网络（CSDN）的约 600 万用户账户【2】
  • DuDuNiu 数据集包括中国一家付费在线游戏网站的约 1600 万个账户
  • 178 数据集包括中国另一个游戏网站的大约 1000 万个密码；所有 3 个中文数据集都是在2011年12月泄露的
  • 6 个数据集总共有大约 6000 万个密码

数据清洗

  • 删除了超过 95 个可打印 ASCII 符的任何密码
  • 删除了长度小于 4 或大于 40 的密码

数据分析

  • 下表 (b) 显示密码在数据集中出现 1、2、3、4、5 次以上的百分比
  • (c) 显示了密码数据集的长度分布，显示最常见的密码长度为 6 到 10，占整个数据集的 87%；CSDN 长度更长——一种解释是，该网站很早就开始实施最小长度为8的密码政策，只有在开始时拥有账户的用户密码才更短
  • (d) 显示了字符分布；字母不是汉语固有的，也因为数字序列在汉语中更容易记忆，以及容易找到与一些容易记住的短语发音相似的数字序列
  • (e) 显示了不同模式的频率；模式分布在不同的数据集上显示出许多差异

image-20210225221622123

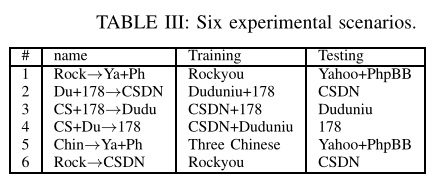
训练与测试场景

  • 反对将所有密码混合为一个大密码集合，因为训练和测试中会导致相似的长度、特征和模式分布

  • 将 Yahoo 和 PhpBB 合并在一起，因为它们规模很小

  • 通过比较场景 5 和场景 1，以及场景 6 和场景 2，可以观察到训练对不匹配数据集的影响

    image-20210226145404013

实验结果

  • 实验结果的表示：猜测数字图、概率阈值图以及 ANLL 表
  • 全字符串模型用 ws 开头
    • $ws-mc-b10$：具有退避和频率阈值 10 的马尔可夫链
    • $ws-mc_i$：i 阶马尔可夫模型，拉普拉斯平滑，$\delta=0.01$
    • -end、-dir 和 -dis 表示三种规范化方法
    • -gts 为 Good-Turing 平滑
  • 基于模板的模型以 tb 开头
    • $tb-co-mc_i$：基于计数的方法将概率分配给模板，用 i 阶马尔可夫模型实例化字段
    • $tb-co-co$：Weir 的 PCFG 从训练集生成字典

实验图

  • (a) 显示 5 阶马尔可夫模型不同正则化方式下，密码排名与概率的图；不同曲线的间隙在 x 增加时逐渐减小，一种猜测是由于每个模型的概率加起来为1，这些曲线必须在某个点相交
  • (b) 显示猜测-数字图；$wc-mc_5-end$、三种 PCFGW 的实例、三种不同模式的 JTR；后二者明显差于前者
  • (c) 将 3 个模型的猜测数曲线和概率阈值曲线绘制在同一图上，如果将猜测数曲线向右移动，可以看到任意模型的猜测数曲线与概率阈值曲线大致匹配
  • (d) 显示了所有基于模板的模型和一个完整字符串模型的概率阈值曲线；使用 DIC-0294 的 PCFGW 性能最差，使用 Openwall 字典的 PCFGW 性能稍好；在 PCFGW 中，从数据集学习比使用现有词典要好。用马尔可夫模型代替计数来实例化片段时，在更高的概率阈值上看到了另一个显著的改进

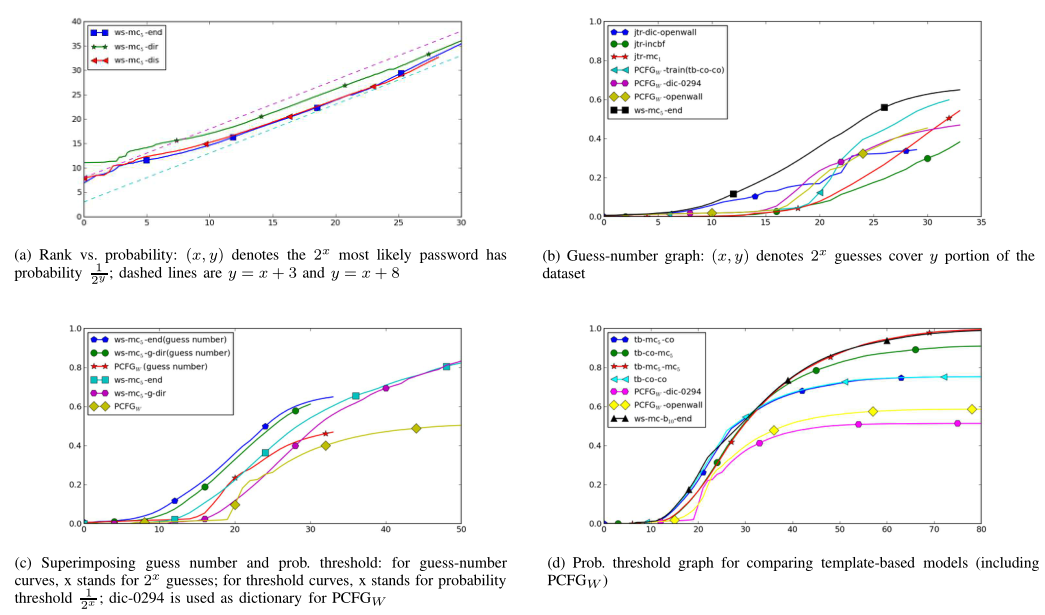
image-20210226195246353

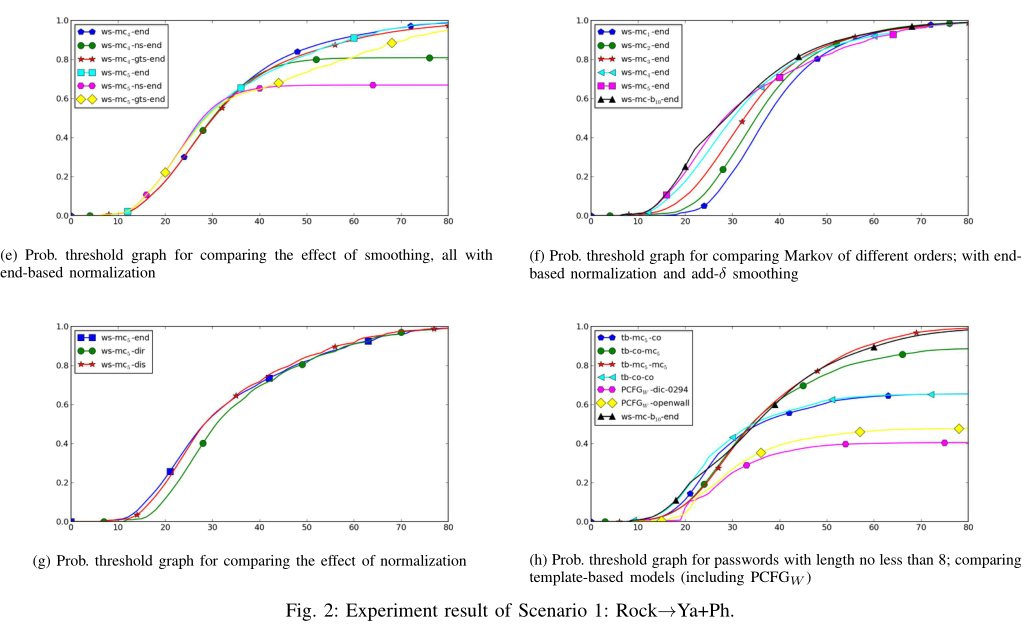
  • (e) 比较了不同平滑方式在 4 阶、5阶马尔可夫模型上的结果
  • (f) 比较了马尔可夫链模型中不同阶数的影响
  • (g) 显示直接归一化性能最差，而基于分布的归一化性能略好于结束符号归一化
  • (h) 仅使用至少8个字符的密码进行评估，结果与 (d) 的曲线相似，因此结果对“密码长度大于8”的网站也有参考性

image-20210226195301634

  • 图 3 与图 4 略

ANLL 表

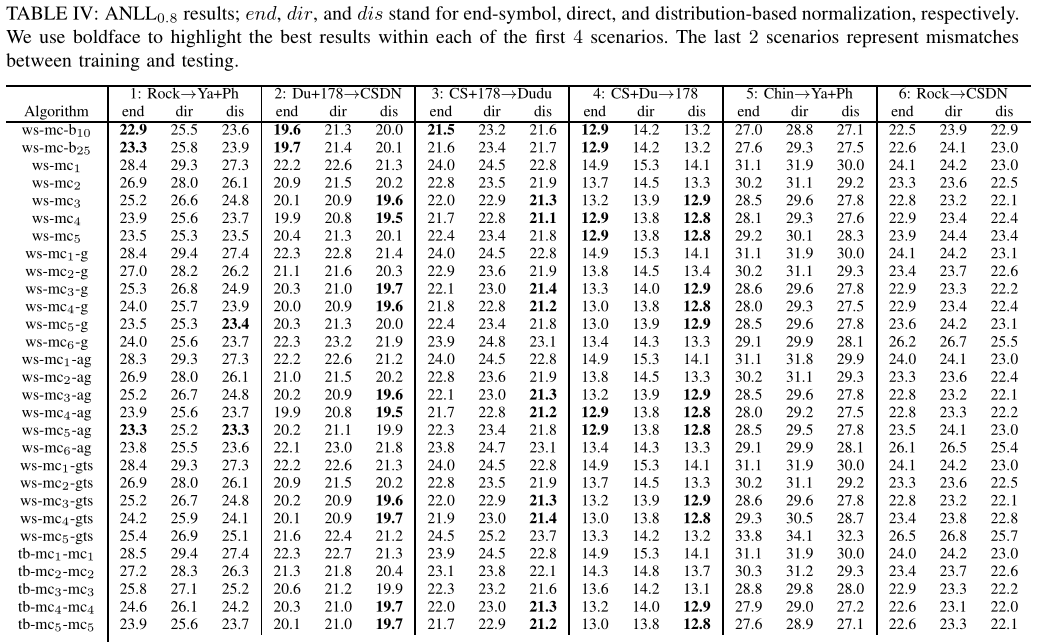
  • 使用结束符号归一化的 backoff 总体上给出了最好的结果——使用一个足够高但又不是太高阶数的马尔可夫，并利用一些方法处理过拟合
  • 对于大多数其他模型，基于分布的归一化执行得最好，其次是结束符号归一化，文献中隐含使用的直接归一化的性能最差；backoff 模型使用变长的马尔可夫链，可以适当地结束密码，而不需要只依赖于密码的长度进行标准化
  • 在平滑效果上，Good-Turing 平滑的表现出人意料地差，特别是高阶马尔可夫链
  • 对于大多数模型，给出最佳结果的马尔可夫链阶数因场景而异
    • 训练数据集略小，则阶数 3 和阶数 4 通常优于阶数 5
    • 中文数据集使用的数字比字母多得多，从而低阶马尔可夫链带来更好的性能
  • 比较场景 5 和 1 以及场景 6 和 2，可以看到在类似数据集上进行训练的重要性
  • 比较场景 2、3 和 4，可以看到 178 显然是 3 个场景中最弱的密码数据集

image-20210226194041132

总结

  • 引入概率阈值图来评估密码数据集
  • 将丰富的统计语言建模文献中的知识和技术引入密码建模
  • 对许多密码模型进行了系统的研究，并获得了一些发现——已经被认为是最先进的并被广泛用于密码研究的 PCFG（Weir 提出的） 模型的性能不如全串马尔可夫模型

参考文献

[1] Passwords, 2009. http://wiki.skullsecurity.org/Passwords.

[2] Csdn cleartext passwords, 2011. http://dazzlepod.com/csdn/.

[3] John the ripper password cracker, 2013. http://www.openwall.com/john/.

[4] Openwall wordlists collection, 2013.http://www.openwall.com/wordlists/.

[5] J. Bonneau. Guessing human-chosen secrets. Thesis, University of Cambridge, 2012.

[6] J. Bonneau. The science of guessing: analyzing an anonymized corpus of 70 million passwords. In Proceedings of IEEE Symposium on Security and Privacy, pages 538–552. IEEE, 2012.

[7] W. E. Burr, D. F. Dodson, and W. T. Polk. Electronic authentication guideline. US Department of Commerce, Technology Administration, National Institute of Standards and Technology, 2004.

[8] C. Castelluccia, M. Dürmuth, and D. Perito. Adaptive password-strength meters from Markov models. In Proceedings of NDSS, 2012.

[9] M. Dell’Amico, P. Michiardi, and Y . Roudier. Password strength: an empirical analysis. In Proceedings of INFOCOM, pages 1–9, 2010.

[10] S. Egelman, A. Sotirakopoulos, I. Muslukhov, K. Beznosov, and C. Herley. Does my password go up to eleven?: The impact of password meters on password selection. In Proceedings of CHI, pages 2379–2388, 2013.

[11] D. Florencio and C. Herley. A large-scale study of web password habits. In Proceedings of WWW, pages 657–666, 2007.

[12] A. Forget, S. Chiasson, P . C. van Oorschot, and R. Biddle. Improving text passwords through persuasion. In Proceedings of SOUPS, pages 1–12, 2008.

[13] W. A. Gale and G. Sampson. Good-turing frequency estimation without tears. Journal of Quantitative Linguistics, 2(1):217–237, 1995.

[14] C. Herley and P. C. van Oorschot. A research agenda acknowledging the persistence of passwords. IEEE Security & Privacy, 10(1):28–36, 2012.

[15] S. Houshmand and S. Aggarwal. Building better passwords using probabilistic techniques. In Proceedings of ACSAC, pages 109–118, 2012.

[16] S. M. Katz. Estimation of probabilities from sparse data for the language model component of a speech recogniser. IEEE Transactions on Acoustics, Speech, and Signal Processing, 35(3):400401, 1987.

[17] P. G. Kelley, S. Komanduri, M. L. Mazurek, R. Shay, T. Vidas, L. Bauer, N. Christin, L. F. Cranor, and J. Lopez. Guess again (and again and again): Measuring password strength by simulating password-cracking algorithms. In IEEE Symposium on Security and Privacy, pages 523–537, 2012.

[18] S. Komanduri, R. Shay, P. G. Kelley, M. L. Mazurek, L. Bauer, N. Christin, L. F. Cranor, and S. Egelman. Of passwords and people: measuring the effect of password-composition policies. In CHI, pages 2595–2604, 2011.

[19] D. Malone and K. Maher. Investigating the distribution of password choices. In Proceedings of WWW, pages 301–310, 2012.

[20] M. L. Mazurek, S. Komanduri, T. Vidas, L. Bauer, N. Christin, L. F. Cranor, P. G. Kelley, R. Shay, and B. Ur. Measuring password guessability for an entire university. In Proceedings of ACM CCS, pages 173–186, Berlin, Germany, 2013. ACM.

[21] A. Narayanan and V . Shmatikov. Fast dictionary attacks on passwords using time-space tradeoff. In Proceedings of ACM CCS, pages 364–372, 2005.

[22] R. Shay, S. Komanduri, P. G. Kelley, P. G. Leon, M. L. Mazurek, L. Bauer, N. Christin, and L. F. Cranor. Encountering stronger password requirements: user attitudes and behaviors. In Proceedings of the Sixth Symposium on Usable Privacy and Security, SOUPS ’10, pages 2:1–2:20, New Y ork, NY , USA, 2010. ACM.

[23] B. Ur, P. G. Kelley, S. Komanduri, J. Lee, M. Maass, M. Mazurek, T. Passaro, R. Shay, T. Vidas, L. Bauer, et al. How does your password measure up? the effect of strength meters on password creation. In Proceedings of USENIX Security Symposium, 2012.

[24] M. Weir, S. Aggarwal, M. Collins, and H. Stern. Testing metrics for password creation policies by attacking large sets of revealed passwords. In Proceedings of the 17th ACM conference on Computer and communications security, pages 162–175, 2010.

[25] M. Weir, S. Aggarwal, B. de Medeiros, and B. Glodek. Password cracking using probabilistic context-free grammars. In IEEE Symposium
on Security and Privacy, pages 391–405, 2009.

[26] Y . Zhang, F. Monrose, and M. K. Reiter. The security of modern password expiration: An algorithmic framework and empirical analysis. In Proceedings of ACM CCS, pages 176–186, 2010.

相关文章推荐