More Than Code

Improved training of wasserstein gans

发表于 分类于
本文字数： 8k 阅读时长 ≈ 7 分钟

《Improved training of wasserstein gans》论文阅读笔记

摘要

  • GAN 是强大的生成模型，但存在训练不稳定性的问题

  • 最近提出的（WGAN）在遗传神经网络的稳定训练方面取得了进展，但有时仍然只能产生较差的样本或无法收敛

  • 这些问题通常是由于在 WGAN 中使用权重剪裁来对判别器实施 Lipschitz 约束

  • 提出了一种权重裁剪的替代方法：惩罚判别器关于其输入的梯度范数

    penalize the norm of gradient of the critic with respect to its input.

    • 比标准的 WGAN 性能更好
    • 能够在几乎没有超参数调整的情况下稳定地训练各种 GAN 体系结构——包括 101 层 ResNets 和具有连续生成器的语言模型

  • 在 CIFAR-10 和 LSUN bedrooms 上实现高质量的生成

  • 代码已开源

介绍

  • 生成对抗网络【9】是一类强大的生成模型，它将生成建模视为两个网络之间的对抗：生成器网络在给定一些噪声源的情况下生成合成数据，鉴别器网络区分生成器的输出和真实数据
  • 许多工作【22，18，2，20】致力于寻找稳定训练的方法
  • 【1】提供了由 GANs 优化的值函数的收敛特性分析
    • 方案命名为 Wasserstein GAN (WGAN) 【2】
    • 利用 Wasserstein 距离产生一个值函数，该值函数具有比原来更好的理论属性
    • WGAN 要求鉴别器必须位于 1-Lipschitz 函数的空间内，作者通过权重剪辑来实现这一点
  • 本文贡献
    • 在数据集 toy 上，演示了判别器权重剪辑如何导致不良行为
    • 提出梯度惩罚
    • 演示各种 GAN 体系结构的稳定训练、相对于权重裁剪的性能改进、高质量的图像生成以及无需任何离散采样的字符级 GAN 语言模型

总结

GAN

  • GAN 训练策略是定义两个竞争网络之间的博弈

    • 生成器网络将噪声源映射到输入空间
    • 鉴别器网络接收生成的样本或真实数据样本，并且必须区分两者

  • 在形式上，生成器 g 和鉴别器 d 之间的博弈是极小极大问题

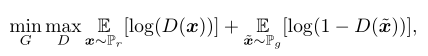
    image-20210323100132297

    • $P_r$是数据分布
    • $P_g$是由 $\widetilde{x}=G(z),z\sim p(z)$ 隐式定义的模型分布，$z$ 是生成器的输入，从一些简单的噪音分布中采样获得（均匀分布或球形高斯分布）

  • 如果鉴别器在每次生成器参数更新之前被训练为最优，最小化值函数等于最小化 $P_g$、$P_r$ 之间的 Jensen-Shannon 散度【9】——-容易导致随着鉴别器饱和，梯度消失

    • 【9】主张训练生成器以最大化$E_{\widetilde{x} \sim P_g}[log(D(\widetilde{x}))]$，在某种程度上规避了这一问题
    • 但即使是这种修正的损失函数，在一个好的鉴别器存在的情况下也会表现不良【1】

WGAN

  • 【2】认为相对于生成器参数而言，GANs 通常最小化的误差函数可能不是连续的，从而导致训练困难

    • 建议改为使用 Wasserstein-1 距离 $W(q,p)$ ——非正式地定义为运输质量的最小损失，以便将分布 q 转换为分布 p （其中损失是质量乘以运输距离）

      which is informally defined as the minimum cost of transporting mass in order to transform the distribution q into the distribution p (where the cost is mass times transport distance).

    • Wasserstein-1 距离处处连续，几乎处处可微

  • WGAN 值函数使用 Kantorovich-Rubinstein 对偶【24】构造

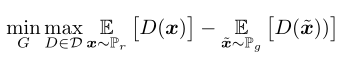
    image-20210323102341999

    • $D$ 是 1-Lipschitz 函数集
    • $P_g$同上
    • 在最佳判别器下，最小化与生成器参数相关的值函数，相当于最小化 $W(P_r,P_g)$
    • WGAN 值函数产生一个判别器函数，判别器与其输入的梯度比其对应的 GAN 表现得更好，使得生成器的优化变得更容易
    • WGAN 具有值函数与样本质量相关的理想属性，而 GANS 并非如此

  • 为了对判别器实施 Lipschitz 约束，【2】建议将判别器的权重限制在一个紧凑的空间内 $[-c,c]$

    • 满足这一约束的函数集是 k-Lipschitz 函数的子集，k 的具体值依赖于 c 和判别器结构

最优 WGAN 判别器的性质

image-20210323104532340

权重约束的问题

  • WGAN 中的权重裁剪会导致优化困难，并且即使优化成功，所得到的判别器也会有一个病态的值表面（pathological value surface）
  • 实验中尝试了多种权重约束，结果显示他们有相似的问题
  • 可通过判别器的批正则化缓解，但深度 WGAN 难以收敛

Capacity underuse

  • 通过权重裁剪实现 k-Lipshitz 约束会使判别器倾向于更简单的函数

  • 使用权重剪裁训练判别器，使其在数个简单分布达到最优，生成器的输入为单位方差高斯噪声。下图为判别器的值表面

    image-20210323133045188

  • 经过权重裁剪训练的判别器忽略数据分布的高阶矩，只对最优函数进行非常简单的近似建模

梯度爆炸和梯度消失

  • 权重约束和损失函数之间的相互作用会导致梯度消失或爆炸，没有仔细调整剪辑阈值 c
  • 证明：在 Swiss Roll toy 数据集上训练 WGAN，改变限幅阈值 c 为 $[10^{-1}、10^{-2}、10^{-3}]$，绘制临界损失梯度相对于连续激活层的范数
    • 生成器和判别器是 12 层 ReLU MLPs，无批处理规范化
  • 下图显示，对于这些值中的每一个，当在网络中向后移动得更远时，梯度要么呈指数增长，要么呈指数衰减

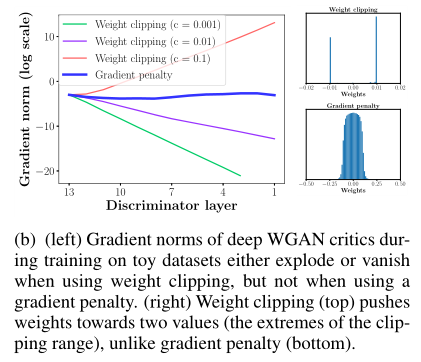
image-20210323133106090

梯度惩罚

  • 提出一种替代方法来实施 Lipschitz 约束

  • 可微函数是 1-Lipschtiz，当且仅当它在任何地方都具有范数至多为 1 的梯度；因此考虑直接约束判别器的输出相对于其输入的梯度范数

  • 对随机样本的梯度范数增加一个软约束

  • 具体如下：

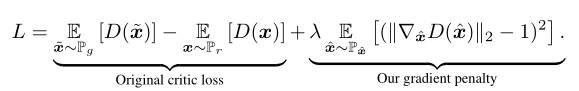
    image-20210323140710029

    • 采样分布
      • 隐含地定义 $P_{\hat{x}}$ 是沿着数据分布 $P_r$ 和生成器分布 $P_g$ 采样的点，两个点之间的直线均匀地进行采样
      • 因为最优的判别器，会包含梯度范数为 1 的直线，而此直线会连接 $P_r$ 与 $P_g$ 之间的点对
      • 考虑到在任何地方实施单位梯度范数约束都很困难，仅沿这些直线实施似乎就足够了
    • 惩罚系数 $\lambda=10$，为实验的结果
    • 判别器不需要批正则化
      • 批正则化将鉴别器问题的形式从将单个输入映射到单个输出，改变为从整批输入映射到一批输出【22】，而本文目标在此情况下不再有效
      • 针对每个输入单独惩罚判别器的梯度
      • 推荐使用层正则化【3】作为批正则化的替代
    • 双向惩罚

  • 算法实现

image-20210323130558424

实验

训练随机体系结构

  • 从 DCGAN 体系结构开始，定义了一组体系结构变体，并进行评估

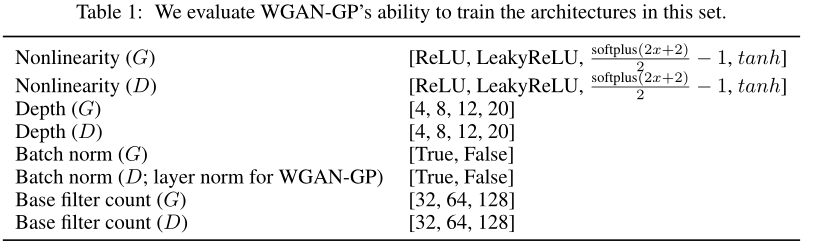
    image-20210323144417597

  • 抽取了 200 个架构样本，并在 ImageNet 上对每个架构进行训练，既有 WGAN-GP 对象，也有标准的 GAN 对象—— WGAN-GP 成功地训练了许多无法用标准 GAN 对象训练的体系结构

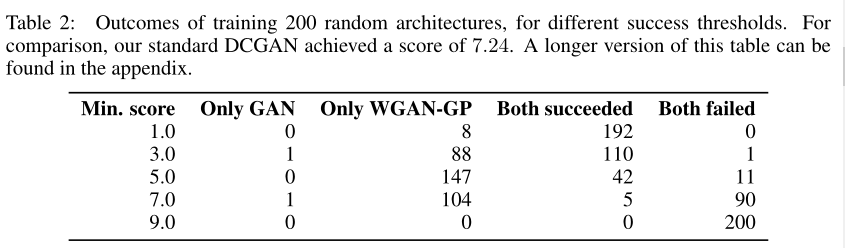
    image-20210323151110156

对不同的体系结构进行 LSUN bedrooms 的训练

  • 在 LSUN bedrooms 数据集【30】上训练六个不同的GAN架构
    • baseline：DCGAN体系结构
    • 生成器中没有 BN 和固定数量的 filters，如【2】
    • 4 层 512 维 RELU MLP 生成器，如【2】
    • 鉴别器或生成器中没有归一化
    • 门控乘法非线性（gated
      multiplicative nonlinearities），如【23】
    • tanh 非线性
    • 101 层 ResNet 生成器
  • 对于每个体系结构，使用四种不同的GAN方法训练模型：WGAN-GP、加权裁剪WGAN、DCGAN【21】和最小二乘GAN【17】
    • 对于每个对象，使用了该工作中推荐的默认优化器超参数集
    • 本文的方法，用层正则化替换鉴别器中的任何批正则化
  • 对每个模型进行了 200K 迭代训练
  • 结果：第一次在 GaN 环境下成功地训练非常深的残差网络

相对于权重剪裁的性能

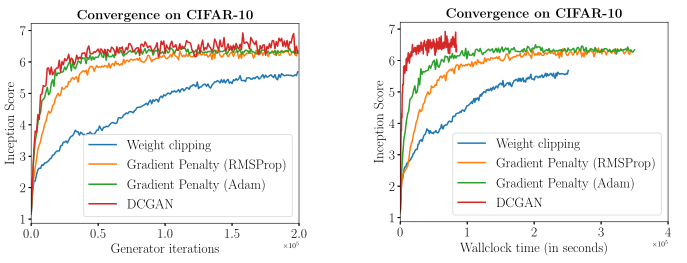
  • 与权重裁剪相比，本文方法的一个优点是提高了训练速度和样本质量

    image-20210323152057681

用连续生成器生成离散数据

  • 为了证明本文的方法对退化分布建模的能力，考虑用具有定义在连续空间上生成器的 GAN 对复杂离散分布建模的问题——在谷歌十亿字数据集【6】上训练了一个字符级的GAN语言模型
  • 生成器是一个简单的 1D CNN ，通过 1D 卷积确定性地将一个潜在向量转换成 32 个独热字符向量的序列。在输出端应用 softmax，但不采样，即在训练期间，softmax 的输出直接传递到判别器；解码样本时，只取每个输出向量的 argmax
  • 模型经常出现拼写错误（可能是因为它必须独立输出每个字符），但还是设法学习了很多关于语言统计的知识。虽然我们并不认为这样做是不可能的，但本文无法产生与标准的 GAN 对象相当的结果
  • WGAN 和其他 GAN 之间的性能差异可以解释（具体解释见原文）
  • 用 GANs 语言建模的其他尝试【31，14，29，5，15，10】通常使用离散模型和梯度估计器【27，12，16】；本文的方法实现起来更简单，尽管不知道它是否能扩展到更复杂的语言模型

损失曲线和过拟合检测

  • 损失与生成质量相关，并且收敛到最小

  • 为了证明本文的方法保留了这一属性，在 LSUN bedrooms 上训练了一个WGAN-GP，并绘制了判别器损失的图像（如下图左边）；当生成器最小化$W(P_r，P_g)$时，损失收敛

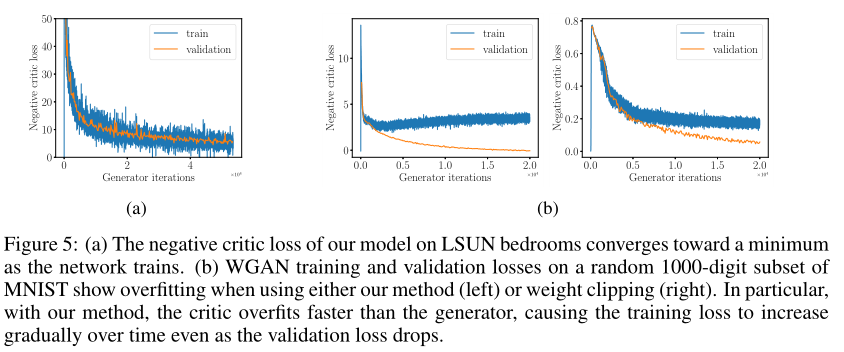
    image-20210323152731029

  • 过拟合：WGAN 和 WGAN-GP 的损失结果不同，这表明判别器过度拟合并提供了一个不准确的 $W(P_r，P_g)$ 估计，但是在 WGAN-GP 中即使验证损失下降，训练损失也会逐渐增加

  • 【28】通过估计生成器的对数似然率来衡量 GANs 中的过度拟合。本文的方法检测判别器（而不是生成器）中的过度拟合，并针对网络最小化的损失来衡量过度拟合

总结

  • 演示了 WGAN 中的权重裁剪问题，并以判别器损失的惩罚项的形式引入了一个替代方案
  • 展示了跨各种体系结构的强大建模性能和稳定性
  • 希望此工作为在大规模图像数据集和语言上更强的建模性能开辟道路
  • 一个有趣的方向是使本文的惩罚项适应标准的遗传神经网络目标函数，在那里它可以通过鼓励鉴别器学习更平滑的决策边界来稳定训练

参考文献

[1] M. Arjovsky and L. Bottou. Towards principled methods for training generative adversarial networks. 2017.

[2] M. Arjovsky, S. Chintala, and L. Bottou. Wasserstein gan. arXiv preprint arXiv:1701.07875, 2017.

[3] J. L. Ba, J. R. Kiros, and G. E. Hinton. Layer normalization. arXiv preprint arXiv:1607.06450, 2016.

[4] D. Berthelot, T. Schumm, and L. Metz. Began: Boundary equilibrium generative adversarial networks. arXiv preprint arXiv:1703.10717, 2017.

[5] T. Che, Y . Li, R. Zhang, R. D. Hjelm, W. Li, Y . Song, and Y . Bengio. Maximum-likelihood augmented discrete generative adversarial networks. arXiv preprint arXiv:1702.07983, 2017.

[6] C. Chelba, T. Mikolov, M. Schuster, Q. Ge, T. Brants, P . Koehn, and T. Robinson. One billion word benchmark for measuring progress in statistical language modeling. arXiv preprint arXiv:1312.3005, 2013.

[7] Z. Dai, A. Almahairi, P . Bachman, E. Hovy, and A. Courville. Calibrating energy-based generative adversarial networks. arXiv preprint arXiv:1702.01691, 2017.

[8] V . Dumoulin, M. I. D. Belghazi, B. Poole, A. Lamb, M. Arjovsky, O. Mastropietro, and A. Courville. Adversarially learned inference. 2017.

[9] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y . Bengio. Generative adversarial nets. In Advances in neural information processing systems, pages 2672–2680, 2014.

[10] R. D. Hjelm, A. P . Jacob, T. Che, K. Cho, and Y . Bengio. Boundary-seeking generative adversarial networks. arXiv preprint arXiv:1702.08431, 2017.

[11] X. Huang, Y . Li, O. Poursaeed, J. Hopcroft, and S. Belongie. Stacked generative adversarial networks. arXiv preprint arXiv:1612.04357, 2016.

[12] E. Jang, S. Gu, and B. Poole. Categorical reparameterization with gumbel-softmax. arXiv preprint arXiv:1611.01144, 2016.

[13] A. Krizhevsky. Learning multiple layers of features from tiny images. 2009.

[14] J. Li, W. Monroe, T. Shi, A. Ritter, and D. Jurafsky. Adversarial learning for neural dialogue generation. arXiv preprint arXiv:1701.06547, 2017.

[15] X. Liang, Z. Hu, H. Zhang, C. Gan, and E. P . Xing. Recurrent topic-transition gan for visual paragraph generation. arXiv preprint arXiv:1703.07022, 2017.

[16] C. J. Maddison, A. Mnih, and Y . W. Teh. The concrete distribution: A continuous relaxation of discrete random variables. arXiv preprint arXiv:1611.00712, 2016.

[17] X. Mao, Q. Li, H. Xie, R. Y . Lau, and Z. Wang. Least squares generative adversarial networks. arXiv preprint arXiv:1611.04076, 2016.

[18] L. Metz, B. Poole, D. Pfau, and J. Sohl-Dickstein. Unrolled generative adversarial networks. arXiv preprint arXiv:1611.02163, 2016.

[19] A. Odena, C. Olah, and J. Shlens. Conditional image synthesis with auxiliary classifier gans. arXiv preprint arXiv:1610.09585, 2016.

[20] B. Poole, A. A. Alemi, J. Sohl-Dickstein, and A. Angelova. Improved generator objectives for gans. arXiv preprint arXiv:1612.02780, 2016.

[21] A. Radford, L. Metz, and S. Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434, 2015.

[22] T. Salimans, I. Goodfellow, W. Zaremba, V . Cheung, A. Radford, and X. Chen. Improved techniques for training gans. In Advances in Neural Information Processing Systems, pages 2226–2234, 2016.

[23] A. van den Oord, N. Kalchbrenner, L. Espeholt, O. Vinyals, A. Graves, et al. Conditional image generation with pixelcnn decoders. In Advances in Neural Information Processing Systems, pages 4790–4798, 2016.

[24] C. Villani. Optimal transport: old and new, volume 338. Springer Science & Business Media, 2008.

[25] D. Wang and Q. Liu. Learning to draw samples: With application to amortized mle for generative adversarial learning. arXiv preprint arXiv:1611.01722, 2016.

[26] D. Warde-Farley and Y . Bengio. Improving generative adversarial networks with denoising feature matching. 2017.

[27] R. J. Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning, 8(3-4):229–256, 1992.

[28] Y . Wu, Y . Burda, R. Salakhutdinov, and R. Grosse. On the quantitative analysis of decoder-based generative models. arXiv preprint arXiv:1611.04273, 2016.

[29] Z. Yang, W. Chen, F. Wang, and B. Xu. Improving neural machine translation with conditional sequence generative adversarial nets. arXiv preprint arXiv:1703.04887, 2017.

[30] F. Y u, A. Seff, Y . Zhang, S. Song, T. Funkhouser, and J. Xiao. Lsun: Construction of a large-scale image dataset using deep learning with humans in the loop. arXiv preprint arXiv:1506.03365, 2015.

[31] L. Y u, W. Zhang, J. Wang, and Y . Y u. Seqgan: sequence generative adversarial nets with policy gradient. arXiv preprint arXiv:1609.05473, 2016.

相关文章推荐