More Than Code

A Security Analysis of Honeywords

发表于 分类于
本文字数： 8.3k 阅读时长 ≈ 8 分钟

《A Security Analysis of Honeywords》论文阅读笔记（NDSS 2018）

摘要

  • 蜜语是与每个用户帐户相关联的诱饵密码，为检测密码泄漏提供了一种有前途的方法
  • 最早由Juels和Rivest在CCS2013上提出
  • 蜜语看似简单，但自动生成难以与真实密码区分的蜜语是一个深刻而复杂的挑战，在Juels的工作中，提出了四种主要的蜜语生成方法，但只有启发式安全参数证明能够生成难以区分的密码
  • 本文首次开发了一系列实际实验，使用10个大规模数据集，总共1.04亿个真实世界的密码，来定量评估四种方法所能提供的安全性
    • 结果显示，它们都无法提供预期的安全性：
      • 通过基本的离线猜测攻击，可以以29.29%到32.62%的成功率，在20个密码（1个真实+19个蜜语）中仅猜测一次就区分真实密码，而不是预期的5%
      • 在利用各种最先进的概率密码模型的高级离线猜测攻击下，能够达到34.21%到49.02%
      • 在一个可以利用受害者个人信息，进行有针对性的猜测攻击环境下，进一步评估了Juels-Rivest方法的安全性：56.81%到67.98%
    • 本文总地解决了由Juels和Rivest定义的蜜语研究中的三个公开问题

介绍

  • 尽管密码在安全性和可用性方面都存在臭名昭著的缺陷，但它仍然是最流行的用户身份验证方法，并有可能在可预见的未来保持其地位
  • 基于密码的身份验证系统的一个固有限制是服务器需要维护一个由所有注册用户的密码组成的敏感文件
  • 即使泄露的密码按照标准惯例存储在加盐散列中，也不会给攻击者造成真正的障碍，通过使用基于现代机器学习的破解算法和通用硬件（如GPU），能够恢复一定量的密码——一旦攻击者获得密码哈希文件，就可以假设大多数密码都可以离线猜测
  • 已经提出了一些方法来完全消除离线密码猜测的可能性
    • 使用机器相关函数（例如，ErsatzPasswords）
    • 采用分布式密码技术（(例如，门限密码认证的秘密共享[7])
    • 使用外部密码强化服务(例如凤凰城[23])。
    • 以上方法都需要对服务器端身份验证系统进行重大更改，并且第一种方法不支持以分布式方式备份密码哈希文件，第二个需要更新客户端系统，不利于用户使用，第三个受到单点故障的影响，可能会向外部泄露用户行为信息
  • 一种更有希望改善这种情况的方法是引入与每个用户的账户相关联的诱饵密码——最早由Juels和Rivest在2013年提出的。他们认为即使攻击者窃取了密码文件并恢复了所有密码，也必须首先从一组k-1有意生成的蜜语中分辨出用户的真实密码，并进行在线登录尝试，此过程极大地阻碍攻击者，而且试图登录时还会在服务器上引发密码文件泄露的警报
  • 此方法对现有服务器端系统的改变少，对客户端系统没有改变，有实用性

挑战与动机

  • 主要的挑战是如何生成不容易与真实密码区分的蜜语
  • Juels-Rivest提出五种蜜词生成方法：四种用于遗留UI，一种用于修改后的UI，并首选前四种（鉴于可用性）——本文也关注遗留UI的蜜语生成
  • 所有的Juels-Rivest方法都是基于随机替换，本质上无法抵抗语义感知攻击
    • 这些方法在多大程度上对语义感知/非感知攻击有效（或无效）从来没有在理论上或经验上量化
    • 大多数关于蜜语的现有技术在评估时仅仅提供启发式的安全性论证，没有严格的理论分析，也没有真实数据集的经验评估——本文将通过实验表明所有蜜语生成方法在很大程度上不能提供预期的安全性
    • [14]给出名为“honeyindex”的改进，但其评估仍然基于启发式的，并受到区分攻击问题和部署问题的困扰
    • [17]从经验上展示了kulback-Leibler散度(KLD)可用来区分真实密码分布和诱饵密码分布，但KLD不适合攻击蜜语的场景——此场景需要区分单个真实密码和一组目标甜言蜜语
  • 此外，在有针对性的猜测攻击下，很少人关注对蜜语安全性的分析——攻击者利用用户选择流行密码的行为、用户的个人身份信息（PII）——随着有针对性的猜测威胁变得越来越多，应当在这种新的威胁下评估蜜语

贡献

  • 离线猜测攻击
    • 首次开发一系列使用大规模真实密码数据的实验来评估[21]中的四种蜜语生成方法，发现它们都无法提供预期的安全性
    • 在一个基本的离线猜测环境下只猜一次，真实密码有29.29%到32.62%的几率被区分，而不是预期的5%
    • 利用最先进的概率密码破解模型（如马尔可夫和PCFG）做猜测攻击，准确率达到34.21%到49.02%。
  • 有针对性的猜测攻击
    • 评估Juels-Rivest的方法在语义感知攻击下的表现——首次通过执行有针对性的猜测攻击来评估蜜语的安全性
    • 如果攻击者知道一些常见的个人信息，如姓名和生日，只需进行一次猜测（当k=20时）就可以以56.8%到67.9%的成功率区分真实密码——回答[21]中“有针对性的攻击在多大程度上有助于识别特定蜜语生成方法的用户密码”
  • 广泛的评估
    • 实验建立在各种概率密码破解模型之上（马尔可夫、TarGuess、PCFG）
    • 使用10个大规模的真实世界密码列表，总共包含1.0436亿个密码，涵盖了各种流行的网络服务
    • 是第一项实证评估甜言蜜语的研究
  • 新的见解
    • 本文发现，生成与用户真实密码的可能性相等的假密码（通过随机替换部分或全部的真实密码字符）是完全不可能的——Juels-Rivest基于随机替换的方法天生就容易受到攻击
    • 本文发现，概率密码模型不适合用于生成蜜语
    • 密码模型可以结合真实数据集，设计有效的实验来评估蜜语的方法——回答了[21]中“有没有好的实验方法来量化蜜语方法的平坦度”的开放性问题

数据集、安全模型和计量

数据集

  • 基于10个大型真实密码数据集评估了Juels-Rivest的蜜语方法

    • 4个来自中文网站，6个来自英文网站
    • 数据集由1.0436亿个纯文本密码组成，涉及9个不同的web服务
    • 纳入三个最近泄露的数据集，可能显示最新的用户密码行为

    image-20211103194455076

    image-20211103194529121

  • 有两个数据集以MD5哈希形式泄露，在一周内通过在一台带有GPU的普通电脑上使用各种离线猜测模型和目标猜测模型TarGuess成功恢复其中的绝大部分

    • Rootkit包含71,228个密码，恢复了其中的97.46%
    • QNB包含97,415个密码，恢复了其中的81.69%——QNB于16年4月从中东的卡塔尔国家银行泄露，据本文所知，这是第一个在学术研究中探索的真实世界银行密码数据集

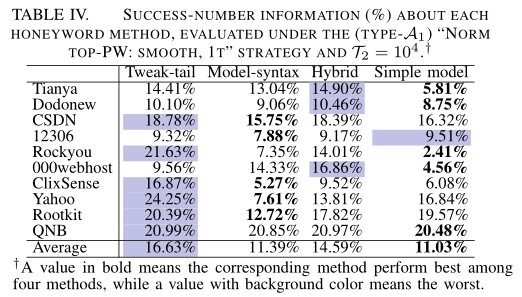
  • 四个密码数据集（12306、ClixSense、Rootkit、QNB）与PII相关联

    • 使用邮箱进一步将不含PII的数据集与含PII的数据集匹配，产生下表第一行所示九个具有PII的密码数据集

      • 四个中文密码数据集：将对应的无PII数据集与12306匹配邮箱获得
      • 四个美英分别是：PII-Rootkit、PII-ClixSense，000webhost和Yahoo与ClixSense匹配得到相关PII
      • PII-QNB：QNB本身
      • 进一步使用两个辅助PII数据集（即Hotel和51job）来扩充每个中文密码数据集——许多账户遗漏一些重要的PII属性，可以通过使用辅助的PII数据集补充

    • 本文使用[30]中type-based PII-tagging来获取PII在密码中的用法

      • 高达36.95%-51.43%的中国用户使用其六种PII中的至少一种来构造密码，美国的英文用户为12.76%-29.94%，中东的英文用户为27.16%——这是因为这里的美国英文用户代表了精通技术的用户
      • 大量用户使用PII来建立密码，合理的蜜语生成方法应该考虑这种用户行为
      • 尽管QNB用户说英语，他们的密码与其他四个英语用户群几乎没有关联——用户分为三组：中文、美国英文和中东英文

      image-20211103200415611

威胁模型

  • 本文考虑客户端-服务器架构的蜜语系统
  • 蜜语系统
    • 涉及到四个实体：一个用户$U_i$、一个身份验证服务器$S$、一个蜜罐检查器和一个攻击者$A$
    • 用户注册了一个账户（$ID_i,\ PW_i$），并由$Gen(k；PW_i)$生成k-1个不同的、看起来像诱饵的密码，[21]中建议k=20
    • 两种类型的蜜语生成方法
      • 基于随机替换，如调整密码尾部
      • 基于密码模型
    • 此时用户在$S$的账户记录为$(ID_i,\ SW_i)$，其中$SW_i=(sw_{i,1},\ sw_{i,2},\ sw_{i,k})$，密码和蜜语通过哈希存储。真实密码的位置用下标来记录，存储在蜜罐检查器中——蜜罐检查器是一个独立的、强化的计算机系统，确保分布式安全，不能公开访问，只能通过“专用和/或加密和认证”的通信通道进行交互
    • 如果用户使用蜜语登录，则报警$S$，不使用蜜语但密码错误则拒绝登录
    • 如果某用户的蜜语登录尝试次数超过阈值$T_1$，则用户必须重设密码
    • 如果所有用户的蜜语登录尝试总数超过预定义的阈值$T_2$，则关闭计算机系统并要求所有用户重置新密码——本文设置$T_2=10^4$
  • 尝试区分蜜语的攻击者
    • $A$的蜜语登录尝试应该尽可能少
    • 假设$A$获得了密码散列文件，知道生成和散列蜜语的算法，拥有所有公开可用的信息——公开泄露的密码数据集和目标站点的密码策略——此类攻击者为类型1攻击者
    • 如果还获得用户PII，此类攻击者为类型2攻击者
  • 其他攻击者
    • [21]认为蜜语面临的其他威胁包括：攻击蜜罐检查器系统、欺骗蜜语系统的DoS攻击以及攻击者利用跨不同系统重复使用的用户密码的交叉攻击
    • 本文不考虑这些

评估指标

  • [21]提出$\epsilon-flat$衡量一个蜜语生成方案安全性
  • $\epsilon-flat$表示给出一个用户的k个蜜语时，攻击者只提交一次密码的最大攻击成功率——当允许用户进行一次以上的在线猜测，即$T_1>1$时)，该度量不足以衡量方法的安全性
  • 本文提出两个新的度量：flatness graph和成功数图（success-number graph），以平均和最坏的角度衡量方法的安全性
    • flatness graph：绘制区分真实密码的概率 vs 用户允许的蜜语尝试次数，即真实密码在前x次猜测中有概率为y的可能被猜中——x=1时的数据点即为$\epsilon-flat$（$x<=k,x<T_1$）
    • success-number graph：绘制成功登录的总尝试次数 vs 错误登录的尝试次数，即第x次蜜语登录尝试前，有y个真实密码被找到，$x<=T_2$——如果各个蜜语的概率和真实密码的概率相似，那么服从几何分布，预期安全性为，攻击者只有1/k的概率猜到密码，将绘制斜率为$\frac{1}{k}$的直线

离线攻击

Juels-Rivest的蜜语生成方案

  • 四种蜜语生成都是基于随机替换的方法——随机替换部分（或全部）真实密码而产生的，前三个取决于真实密码的结构
  • Tweaking by tail：
    • “调整”真实密码的所选字符位置，以生成k-1个蜜语
    • $t$表示需要调整的位置数，[21]主要讨论了“尾部修改”
    • $pw_i$的最后$t$个位置中的每个字符都被随机选择的相同类型的字符替换：数字被数字替换，字母被字母替换——trustno1，t=3，则蜜语是trustyp0、trustmi7等
  • Modeling syntax：
    • 将$pw_i$分割，标记为相同类型的连续字符并提取相应的语法，通过随机选择的与语法匹配的值替换标记来生成蜜语
    • trustno1抽象L7D1，生成dfdphus3、letmein4等
  • Hybrid：
    • 将前二者合并
    • 采用Modeling syntax提取$pw_i$的语法并生成a个种子蜜语（包括$pw_i$），通过调整每个种子蜜语来生成b-1个蜜语，最后，从a*(b-1)个蜜语中随机选择$pw_i$之外的k-1个蜜语
    • 假设k=20，a=4，b=5：trustno1抽取语法L7D1，生成3个种子蜜语dfdphus3、letmein4和kebrton9，通过尾部调整从4个种子蜜语中各产生4个新的蜜语，合计产生20个蜜语
  • Simple model：
    • 使用真实的密码样本来帮助生成蜜语
    • 根据现实生活密码和8%的不同长度随机密码建立一个列表，从列表选取一个长度为d的随机元素$w=w_1w_2…w_d$，启发式地生成一个带有字符序列$w_1c_2…c_d$的蜜语
    • 后面d-1个字符，$c_i$用L中随机元素的$w_i$替换的概率为10%，保持不变的概率为50%，在$c_{i-1}=w_{i-1}$的前提下用$c_i$替换$w_i$的概率为40%

两种攻击方式

  • 提出两个蜜词区分策略，本质上不同于现有的启发式策略
  • 利用用户选择的密码遵循齐夫定律的事实，并根据一些已知的概率分布对蜜语进行排序，无论这些概率分布是否在用户内部标准化——概率分布从泄露的密码数据集中计算，或者基于概率密码模型获得

Top-PW attack

  • $A$按照概率递减顺序依次尝试$n*k$个蜜语（包含真实密码在内），每个尝试密码$sw_{i,j}$的概率来自一个已知的概率分布$P_D$，$D$是一个泄露的密码集合：

    • 如果$sw_{i,j} \in D$，设置$Pr(sw_{i,j})=P_D(sw_{i,j})$
    • 否者设置$Pr(sw_{i,j})=0$
    • 其中$P_D(x)=\frac{Count(x)}{|D|}$

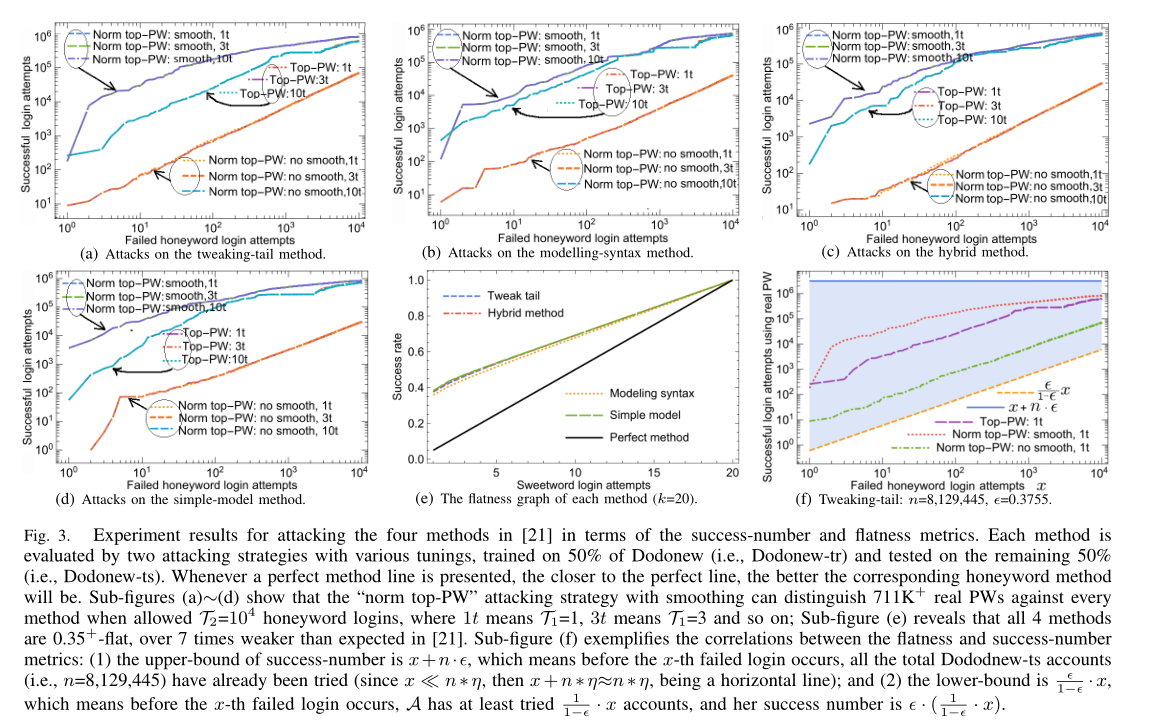
  • 将DuDuNiu分割为相等的两份，分别为训练和测试；为测试部分的每个密码，分别根据上面的四种方法生成$k-1$个蜜语，$P_D$来自训练部分

  • 图a-d结果显示本攻击能够区分测试集中至少615664的真实密码，但根据[21]的说法，攻击者理应最多区分出$T_2/(k-1)$个真实密码，即在success-number标准下，[21]的方案均比预想的安全性差

  • 图e显示，给定某个用户的k个蜜语（包括真实密码），根据上面的方法排列各个蜜语概率，选取概率最大蜜语进行登录尝试，有35%的几率一次成功

  • 这一识别过程与$sw_{i,j}$所属的蜜语列表的性质没有什么关系，即如果蜜语列表$SW_i$中一个蜜语概率为0.03其他为0.029，蜜语列表$SW_j$中一个蜜语概率为0.028其他为0.001，则应当先使用$SW_j$中概率0.028的蜜语尝试破解用户$U_j$的账户——即为下面的方法

    image-20211104104301340

Normalized top-PW attack

  • 与上述不同的是，攻击者根据归一化概率的降序尝试蜜语：$sw_{i,j}$的概率来自一个已知的密码分布$P_D$

    • 如果$sw_{i,j} \in D$，设置$Pr(sw_{i,j})=P_D(sw_{i,j})$
    • 否者设置$Pr(sw_{i,j})=0$
    • 设置$P_r(sw_{i,j})=\frac{P_r(sw_{i,j})}{\sum_{t=1}^kPr(sw_{i,t})}$
    • 若系统的$T_1>1$，则每当一个$SW_i$的蜜语经过尝试后，其他没有尝试的蜜语的概率需要归一化为：
      • 任意的$sw_{i,j}\in SW_i$且不在尝试过的蜜语集合$L$中，$Pr(sw_{i,j})=Pr(sw_{i,j})/\sum_{t\notin L}Pr(sw_{i,t})$

  • 以上步骤为下面算法1的line 5，算法1可用于生成success-number graph

    image-20211104110835878

  • 以上步骤为下面算法2的line 5，算法1可用于生成flatness graph

    image-20211104110821105

  • 以上可能导致很多蜜语的概率为0——但不应该认为没见过的东西概率为0，此时稀疏性较高，因此设置一种+1平滑：如果$sw_{i,j} \notin D$，设置$Pr(sw_{i,j})=\frac{1}{|D|+1}$，实验表明此平滑优于Laplace等平滑策略

  • 标准化的过程，对success-number有较大影响，但对flatness graph没什么影响，因为不会更改一个$SW_i$内部的相对排名

  • 本文认为，关键在于如何对$k$个蜜语排序

  • 以上两个方法在区分热门蜜语和冷门蜜语是有效的，因此当热门蜜语更可能是用户密码时，以上策略有效——它们适合攻击不基于密码模型的方法，例如[21]的四个方法，这些方法生成的k-1个蜜语通常比用户的原始密码概率的更低

实验设置

  • 各个评估的不同之处在于，上面的方法（算法1、2的line 5）是怎么初始化的：

    • 攻击的策略
    • 训练集和测试集
    • 此外，对每个攻击策略，还有7种不同的密码模型：list、PCFG、马尔可夫、三者的TarGuess版本、no-training-set

  • 训练集和测试集都是对半开

  • 所有的图种，线越低，相应的蜜语策略越好

基本的离线攻击

  • 设置密码模型为List，即$P_D(x)=\frac{Count(x)}{|D|}$

  • 测试结果即为上面的Fig3(a)-(d)——结果显示平滑与标准化极为重要

  • Model-syntax>Simple model=Hybrid>Tweak-tail

    image-20211104113634092

  • 本文方法如此有效的原因，是因为能够区分热门蜜语和冷门蜜语，下表说明，DuDuNew的测试集中，最热门的密码极少（小于0.01%）由[21]的任何方法生成

    image-20211104113905049

进一步评估

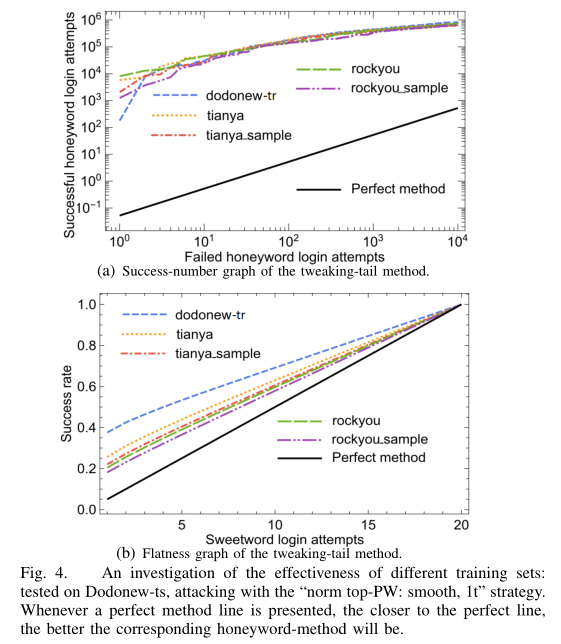
不同的训练集

  • 训练集和测试集来自不同的库

  • 结论：

    • 训练集和测试集越接近，攻击越有效
    • 训练集越大，攻击越有效
    • 四种蜜语生成方法的安全性远低于预期

    image-20211104122006746

攻击基于密码模型的方法

  • [21]的四个方法基于随机替换

  • 本文使用PCFG为例，用PCFG构建蜜语生成方法

    • 对于给定用户的密码$PW_i$，k-1个蜜语通过在指定数据集$D$上训练的PCFG模型（记作$P_{PCFG(D)}(\cdot)$）生成，此时k-1个蜜语独立于$PW_i$

    • 此时热门蜜语一般不会更有可能是真正的密码，因为现在生成k-1个蜜语完全依赖于密码模型而不是$PW_i$

    • 为此，修改Norm top-PW策略，提出Norm PW-model攻击策略：

      • 设置基本相同

      • 最开始将密码列表应用于模型，得到$PCFG(D)$

        the known password distribution D(e.g., a leaked password list) is first applied to the PCFG model (we use the laplace smoothing, see [24]), and this results in a password distribution PCFG(D).

      • 在标准化时，设置：

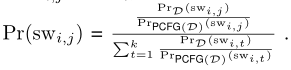
        image-20211104131503103

  • 马尔可夫模型同理

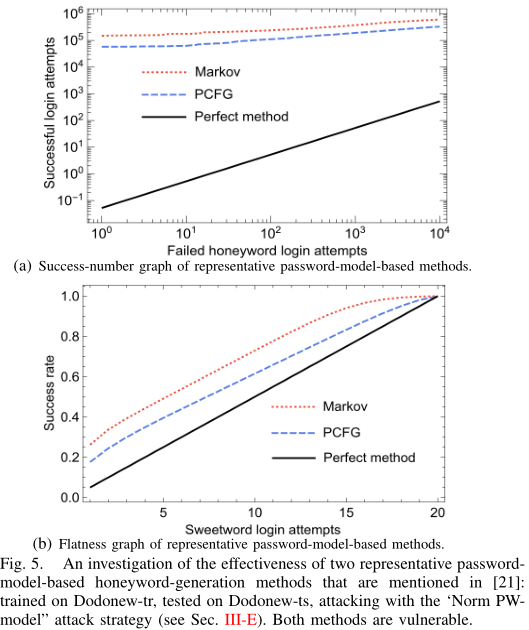
    image-20211104131612889

image-20211104131737745

  • 结果显示，用PCFG生成蜜语，其安全性确实会提升，但仍不是预期的安全性

高级离线攻击

  • 以上均基于List的攻击模型，即获得一个密码list后，统计蜜语的概率，排序，攻击，区别在于蜜语是如何生成的

  • 下面的实验，构建其他的攻击模型，来破解基于Tweak-tail的蜜语生成方法

  • no-training-set：

    • 蜜语的分布$Pr_{SW}$由真实密码分布$Pr_{PW}$和蜜语密码分布$Pr_{HW}$组成，且：

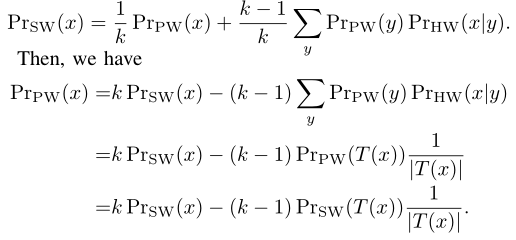
      image-20211104132808725

      • $Pr_{SW}$的分布可近似为$\frac{count_{SW}(x)}{count_{SW}}$，因此得到$Pr_{PW}(x)$的估计：

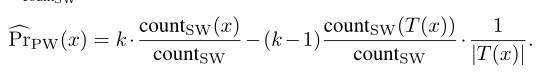
        image-20211104132940891

    • 采用5个不同方式进行平滑

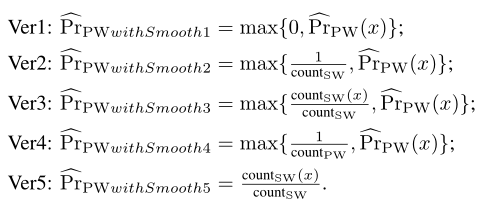
      image-20211104133930121

  • 对PCFG使用Laplace平滑，对马尔可夫使用back-off平滑

  • 实验的设置与Norm top-PW类似，但是：将泄露密码集首先应用到马尔可夫或PCFG上，得到密码分布$Markov(D)$和$PCFG(D)$，之后用$P_{Markov(D)}(\cdot)$来对密码分配概率

  • 实验结果如下所示：

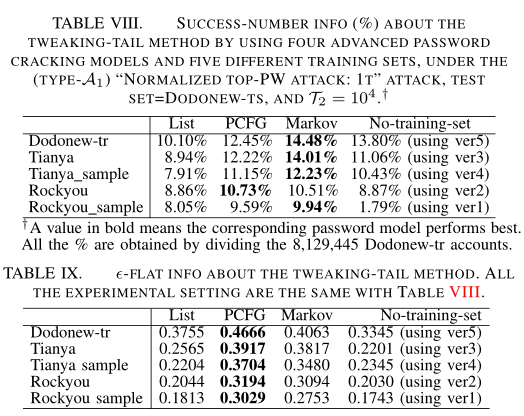
    image-20211104134000249

Targeted猜测攻击

  • 攻击者掌握用户的PII

  • 采用三种有针对性的密码破解模型：TarPCFG [30]，TarList和TarMarkov

    • TarPCFG是[30]中的TarGuess-I，TarList和TarMarkov分别是PII-enriched马尔可夫模型和List模型
    • TarMarkov模型通过应用[30]中提出的基于类型的PII段匹配方法从Markov模型转换而来，只需要将各种在[30]中定义的基于类型的PII标签，合并到Markov模型的字母表中，其余操作都与字母表中的原有字符相同
    • TarList模型的转换类似

  • 与”Norm top-PW: smooth, 1t“的设置相似，但已知的密码集用于训练TarPCFG模型，并用$P_{TarPCFG}$替代$P_D$，其他两个同理；模型在PII-DuDuNiu训练和测试

    image-20211104143954463

总结

  • 首次实证评估了Juels和Rivest在CCS’13上提出的四种主要的蜜语生成方法，结果表明，他们的方法都不满足预期的安全级别
  • 本文工作首次给出了全面、令人信服的量化证据，证明了最先进的蜜语生成方法有多脆弱，突出了蜜语研究看似简单的本质——自动生成难以与真实密码区分的蜜语并不容易，但却是一个巨大的挑战
  • 由于所研究的四种蜜语生成方法的局限性不能轻易解决，本文认为实现主动和及时的泄露检测具有广泛的意义
相关文章推荐