More Than Code

密码协议(1) 引论与密钥交换协议

发表于 分类于
本文字数： 2.3k 阅读时长 ≈ 2 分钟

《密码协议》课程笔记（1） 引论+密钥交换协议

引论

密码协议基础

  • 协议：两个或者两个以上的参与者为了达到特定的目的，采取的一系列步骤（没有严格的界限来区分密码协议和一般协议）
    • 规定了一系列有序执行的步骤
    • 有两个或者两个以上的参与者
    • 协议都有明确的目的
  • 密码协议的要求：
    • 安全需求——加密（执行过程中的敏感数据不被非授权者所知）、认证（保证参与者的合法身份）和不可抵赖性（协议执行过程可以追查）
    • 鲁棒性——有恶意参与者时能部分地正确执行
  • 分类：
    • 仲裁协议——仲裁者是可信第三方，协议的执行一直需要仲裁者
    • 裁决协议——裁决者只在有争议的时候才参与协议的执行
    • 自动执行协议——协议本身公平，不需要可信第三方

密码协议模型

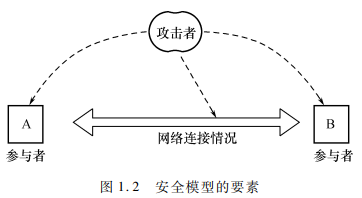
image-20220327203810799
  • 参与密码协议的主体：协议参与者、协议攻击者、可信第三方（协议参与者都信任的一个主体或者一个组织）、仲裁者——攻击者和参与者没有严格的界限
  • 网络可能是同步的，也可能是非同步的。同步网络中，所有信息在某一个时钟周期内传送。大部分密码协议的研究都在同步网络条件下
  • 参与者分为诚实参与者、半诚实参与者和恶意攻击者
  • 攻击者的能力：拥有无限计算能力的攻击者，只有概念多项式时间计算能力的攻击者——信息论安全的、密码学安全的
    • 安全信道：参与者的通信既不会被攻击者窃听，也不会被攻击者篡改
    • 认证的信道：攻击者可以窃听参与者的通信，但是不能篡改通信内容
    • 未认证的信道：窃听+篡改
    • 被动攻击者（窃听者）：只是窃听或获取不诚实参与者在协议进行中的所有输入，不控制其行为
    • 主动攻击者：窃听+控制行为

密码协议设计分析概述

  • 密码协议安全性分析的基本方法：
    • 使用自然语言论证的标准模型
    • 开发专家系统
    • 使用Random Oracle模型
    • 使用BAN类逻辑
    • 使用CSP（Communicating Sequential Processes）等模型检查方法

密钥交换协议

数学前提

  • 随机变量X、Y之间的统计距离：

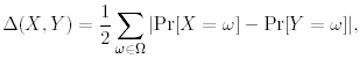
    image-20220426142423867
    • $\Omega$为变量X和Y的采样空间
    • 统计距离为1，当且仅当X和Y不相容（每个随机事件$\omega$，要么X发生，要么Y发生）
    • $0\leq\Delta(X,Y)\leq 1, \Delta(X,X)=0,\Delta(X,Y)=\Delta(Y,X),\Delta(X,Y)+\Delta(Y,Z)\geq \Delta(X,Z)$

  • 三种假设：

    • Discrete Logarithm DL假设（给$g^x$，难求$x$）
    • (Computational) Diffie-Hellman DH假设（给$g,\ g^x,\ g^y$，难求$g^{xy}$）
    • Decision Diffie-Hellman DDH假设（知道$g,\ g^x,\ g^y,\ g^z$，难以确定是否$z=xy\ mod\ n$）
    • 证明困难程度依次下降

  • 随机自规约：一个问题的实例$I$满足：

    • $I$构造出一个或多个随机实例$I’$，后者是独立于前者的均匀分布
    • 如果得到随机实例的解，则从$I’$的解得到$I$的答案
    • 以上两步要在多项式时间内完成
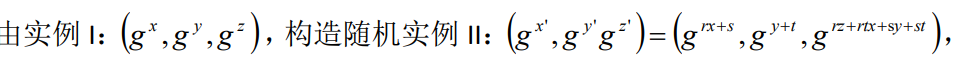
    image-20220328132907732 image-20220328132946056 image-20220428122506270

  • 计算安全的形式：一个方案为$(t,\epsilon)$安全，如果每个运行时间最多为t的攻击者最多以$\epsilon$的概率攻破——当运行时间和成功概率为安全参数n（双方生成密钥时，以n为安全参数，攻击者也知道）的函数时：

    • 多项式时间概率算法：多项式时间内运行的概率算法
      • 多项式时间算法：在最坏情况下时间复杂度为$O(n^k)$的算法，n为问题规模，k为常数
      • 多项式时间算法的基础上，还允许算法获取到随机数（另一种表述为，算法执行中存在一个随机选择下一步的过程，相同输入经过该算法可能会得到不同结果）
    • 可忽视函数：（小的成功概率，指比任何关于n的多项式的倒数级别更小）比任何多项式的倒数都增长得慢的函数，称为可忽略的，例如$2^{-n}$
    image-20220426151856426
    • 渐进安全：如果每一个PPT（概率多项式时间）攻击者攻破一个方案的概率是可忽略的，则方案是安全的

密钥交换

密钥交换也称密钥协商，利用此类协议，通信双方（或多方）在一个公开信道上相互传递某些信息建立一个共享的密钥，用于对称密码协议，实现保密性、数据完整性等密码服务。

有些密钥交换协议会假设Ａ和Ｂ在运行协议前已经共享了一个密钥。

两方Diffie-Hellman密钥交换

  • 协议内容

    • 双方约定素数阶有限域$F_p$和其乘法循环群一个生成元$g$

      image-20220328133644178

    • 将协商出的共享秘密值$k$用于一个哈希函数的输入，其输出作为会话密钥——因为k是循环群中的元素，不能直接用作对称密钥，并且可能存在较多冗余，哈希函数能够去除这种冗余

  • 被动攻击：能够抵御

    • 安全性依赖于求解离散对数（CDH）问题的困难性——攻击者截取$g,g_a,g_b$，求解$k=g^{ab}$
    • 必须假设使用的循环群中DDH问题是困难的——攻击者只想知道与$k$有关的任何信息

  • 中间人攻击：

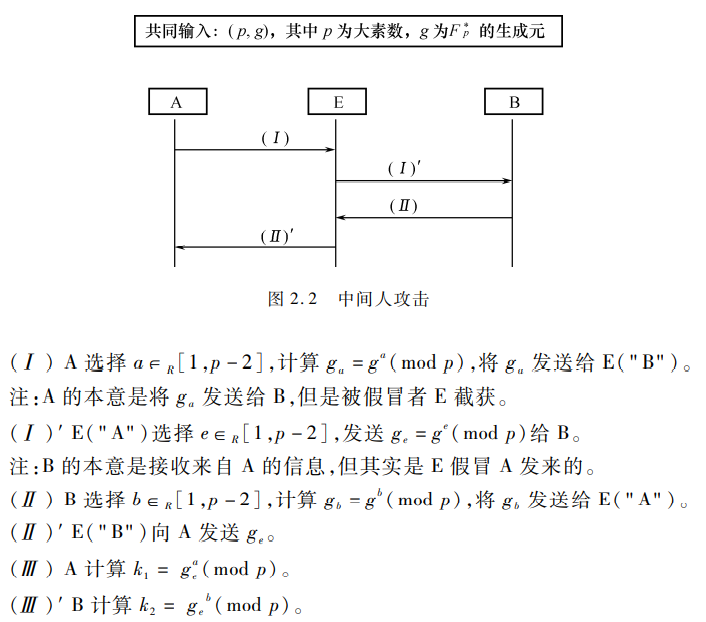
    image-20220328134606212
    • 此时攻击者E就可以计算$k_1=g_a^e\ mod\ p$和$k_2=g_b^e\ mod\ p$
    • 不具有密钥的认证功能——协议参与者没有对收到的信息进行认证，以确信消息确实来自认定的通信方

  • 端到端协议（station-to-station）：对Diffie-Hellman的改进，假设Torrent为可信中心

    • 约定：

      image-20220328140101876

    • 过程：（使用参与方的数字签名保证信息来源真实性）

      image-20220328140151147

  • 基于密码加密的协议

    • 假设两个参与者共享一个口令
    • $E$为一个加密算法，以口令和消息作为输入，输出为密文，记为$C=E_{pw}(m)$；$D$为解码算法
    • 过程：
      • 参与者A选择均匀选择一个$x_A\in Z_n$，发送$E_{pw}(y_A),y_A=g^{x_A}$给B
      • 类似的，参与者B也发送$E_{pw}(y_B)$给A
      • 则共享密钥为$k=g^{x_Ax_B}$
    • 被动攻击者只能看到加密后的内容，不会泄露pw的信息，而且$x_A$服从均匀分布，也是未知的
    • 主动攻击者需要猜出pw，才能实现中间人攻击
相关文章推荐