《密码协议》课程笔记(3) 身份认证协议
身份认证协议
认证是一个通信过程,一个实体(验证者)B验证了另一个实体(声称者/原告)A声称的某种属性。若认证是验证消息的某种声称属性,则称为数据源认证或消息认证;若认证是验证原告声称的身份,则称为实体认证——实体认证是指通过一个通信过程或协议, 一个实体B和另一个实体A建立一种真实通信,使得B能够验证A是要与之通信的实体。
也可以将A的身份当作一条消息来处理。
基本概念
一些差别:
- 与消息验证相比,没有消息的新鲜性
- 与数字签名相比,没有不可否认性
- 与经过身份验证的密钥交换相比,不需要实际地建立安全密钥
好的身份鉴别协议要满足:
- 可靠性
- 不可转让性
- 不可冒充性
鉴别方案包括两类协议:登记/注册(registration)、身份鉴别(identification)
对称身份鉴别方案:注册过程以双方共享一个密钥结束,双方都要存储该密钥
非对称身份鉴别方案:注册过程以双方共享一对公钥结束,证明者才知道私钥——证明者可以和多个验证者共享公钥对
攻击方法(假设注册过程是安全的):
impersonation attack:鉴别协议最基本的安全要求是能抵御伪装攻击,即攻击者无法让自己被鉴别为任意参与者
- 被动:窃听证明者和验证者的通信,或者在非对称方案中从公钥分析出私钥
- 主动
- 猜测攻击:攻击者冒充证明者,希望在不知道密钥或私钥时做出正确猜测
- cheating verifier attack:攻击者冒充验证者,希望通过违反协议过程,从证明者的反馈中提取有效信息
中间人攻击
grandmaster chess attack:业余选手与两位大师比赛象棋,一场为白棋另一场为黑棋,只需将所有动作从一位大师复制到另一位大师即可——无论如何,都可以获得一些信息
实例
基于密码的鉴别方案:对称的身份鉴别方案,但无法抵御窃听攻击(注册后,证明者获得唯一的用户id,鉴别时,证明者向验证者发送用户id和密码)
Hash chain(用于解决窃听攻击)
- 长为n的序列,满足:$x_{i+1}=H(x_i)$,其中哈希函数将0/1比特映射为长为k的比特串
- 注册阶段:
- 证明者选择$x_0\in{0,1}^k$,计算$x_n=H^n(x_0)$,发给验证者
- 证明者和验证者均初始化一个计数器$i=1$
- 证明者存储$x_0$,验证者存储$v=x_n$
- 验证阶段:
- 证明者计算$x_{n-i}=H^{n-i}(x_0)$并发送给验证者,证明者的计数器加一
- 验证者测试$H(x_{n-i})=v$
- 若验证成功,则验证者计数器加一,并且$v=x_{n-i}$
- 若验证失败,则认为证明者身份非法
- 可以视为对称方案;猜测攻击不可行,而窃听攻击无法做下一步的验证
基本的挑战响应协议
验证者发送一个随机的挑战,证明者应答,验证者确认应答
四种挑战响应方案
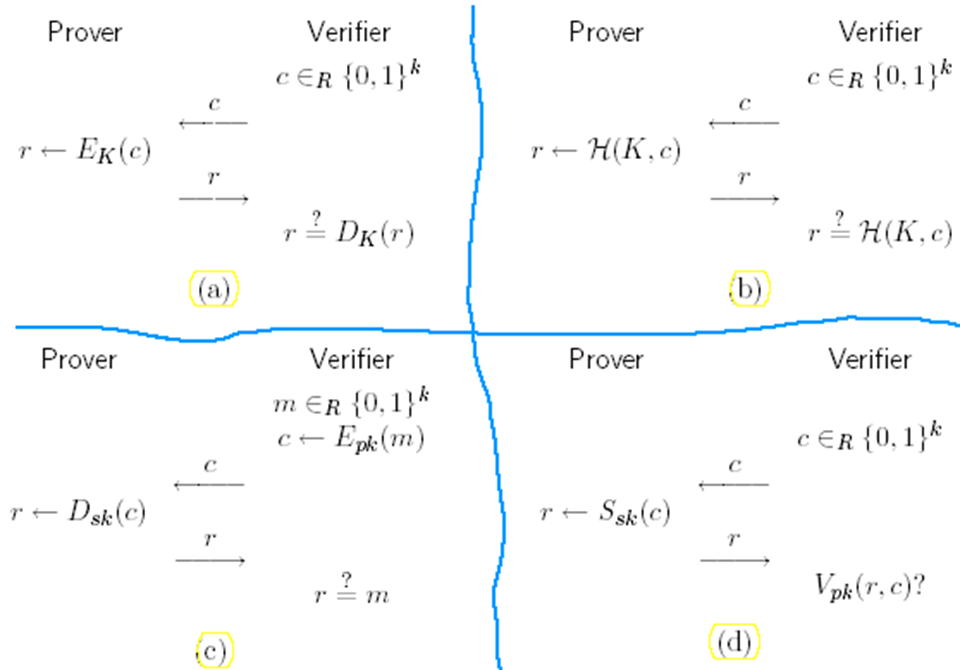
方案1:为了抵御窃听攻击,加密方案必须抵御已知的明文攻击;为了抵御欺骗验证器攻击,加密方案必须抵抗自适应选择明文攻击

方案2:H表示一个哈希函数;能够抵御窃听攻击和欺骗验证者攻击
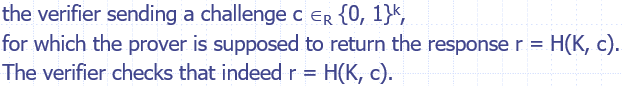
方案3:双方共享一个公钥,证明者有私钥;加密方案必须能抵御窃听攻击与欺骗验证者攻击

方案4:双方共享一个公钥,证明者持有私钥,使用私钥做签名,验证者通过公钥验证签名;签名方案必须能抵御窃听攻击与欺骗验证者攻击

以上方案是安全的,当且仅当加密或验证方案是安全的——加密和签名的开销大
零知识验证方案(Schnorr’s Zero-knowledge Protocol)
无论验证者怎么作弊,都无法从诚实的证明者获取有用信息,但诚实验证者可以确信证明者知道私钥——验证者通过与证明者交互得到的信息,也可由验证者模拟产生
举例:Schnorr’s protocal
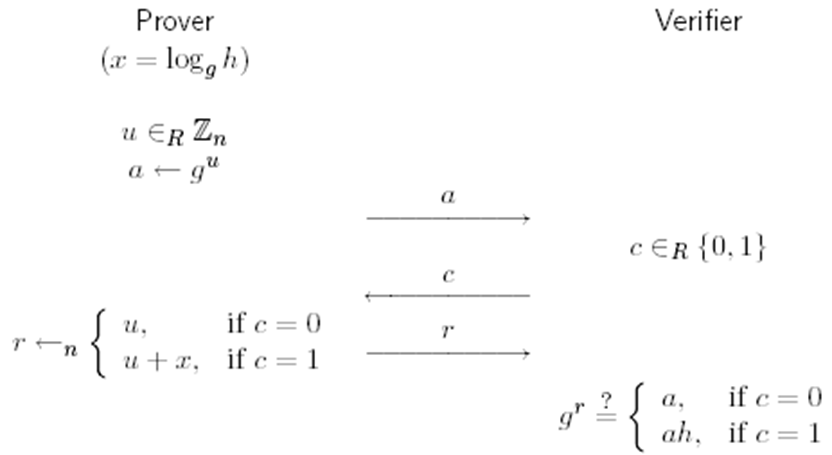
G是阶为n的群,生成元为g,n为大素数,$x\in Z_n$是证明者的私钥,$h=g^x$为证明者的公钥,在注册阶段,验证者获得公钥
上图为身份验证的一次迭代,双方会进行k轮迭代,k是一个安全参数
第一个消息a称为承诺(commitment),第二个消息c称为挑战(challenge),第三个消息r称为回应(response)
向验证者表明,证明者知道私钥$x=log_gh$(soundness property):
- 如果证明者不知道x,则证明者最多能准备一个a,用于c=0和c=1的场景。当c=0时,作弊的证明者设置$a=g^u$,发送$r=u$;当c=1时,作弊的证明者设置$a=g^u/h$并发送$r=u$,此时能满足验证者的要求$g^r=ah$,但证明者无法准备好这样的a——假设能够满足以上两个情况,则证明者能够产生两个不同的$r$,即有$g^{r_0}=a,g^{r_1}=ah$,即$h=g^{r_1-r_0}$,但因为$x=r_1-r_0\ mod\ n$,表明证明者知道x
- 每一轮,作弊的证明者有50%的可能不被发现,因此经过k轮,不被发现的概率只有$2^{-k}$
为什么是零知识?
作弊的验证者可以多次参与协议,每次迭代中都获得一组(a,c,r),但实际上验证者完全可以自己生成(a,c,r)而不需要交互——模拟产生(a,c,r)和诚实证明者、诚实验证者交互输出的(a,c,r),概率分布相同

无论作弊的验证器采用什么算法提取信息,都可以使用相同的算法生成相同分布的信息,而无需证明者的参与(真实的输出是使用私钥x作为输入生成,而模拟的输出仅使用公钥h作为输入生成)
进一步改进:c的选择范围更大——此时仍然soundness,但不是零知识(Schnorr’s protocol is sound and honest-verifier zero-knowledge. Although it cannot be proved zero-knowledge, no attacks are known for this protocol)