More Than Code

密码协议(4) 零知识证明协议

发表于 分类于
本文字数： 4.2k 阅读时长 ≈ 4 分钟

《密码协议》课程笔记（4） 零知识证明协议

零知识证明协议

理论前提

  • 介绍：

    • 参与者：证明者、验证者
    • 证明者不透露任何超出命题真实性的信息的情况下，使验证者相信命题的有效性（命题类似于”我知道这个公钥的私钥，而且在任何情况下，私钥都是不同的”）——互不信任的各方的沟通

  • 证明：

    • NP可以被描述为一组语言，存在一个有效的过程来检查（而不是计算）一个字符串是否属于该语言

      • 给定一个来自语言L的字符串x和证书y，易检查x是否属于L
      • 定义为，一组可以在多项式时间内，被非确定性图灵机识别的语言（确定性图灵机TM模拟非确定性图灵机NTM的方法，和用确定性有限自动机DFA模拟非确定性有限自动机NFA的模拟方法相同）

    • 确定性有限自动机DFA：对当前状态，给定一个输入能确定下一个状态

      image-20220401184203211

    • 非确定有限自动机NFA：对当前状态，给定一个输入时下一个状态可能有多个

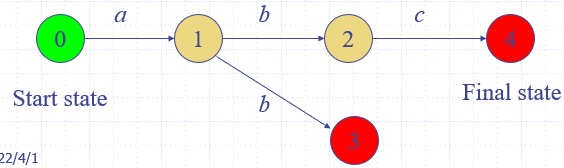
      image-20220401184149762

    • 模拟过程：本质上按顺序遍历搜索树

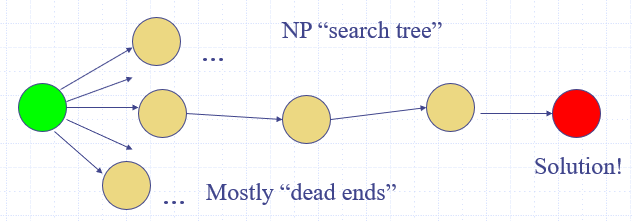
      image-20220401184343083
      • final states：NFA中所有的final state
      • 如果告知，某条能到达final state的路径在搜索树里，此时可以直接验证

    • 证明系统举例：

      • 给定一个公式：$(x&&y&&z)||(x&&y)||z$
      • 证明者必须证明这个公式能够等于True，一般而言，证明者确实能够找到这样的一组$x,y,z$
      • 验证者只需要收到赋值后，检查公式是否为True，以验证证明者是否正确——这只需要多项式时间

    • 证明系统的性质：

      • 验证者的策略有效
      • 完整性（正确的断言会有一个令人信服的证明策略），可靠性soundness（错误的断言不存在证明策略）
      • Goedel’s incompleteness theorem——任何“足够复杂”的证明系统，不可能既完整又可靠

  • 知识：Bob在与Alice互动后获得知识，如果：在交互之后，Bob可以轻松地计算一些之前对他来说很难的东西

  • 交互式证明：

    • 上面的证明系统+允许双方通话+允许验证者投硬币
      • 完整性：如果x在L中，接受的概率大于等于2/3
      • 可靠性：如果x不在L中，接受的概率小于等于1/3
    • 验证者的策略是一个概率多项式时间的过程
    • 验证者的计算能力不受资源限制

  • 零知识证明：

    • 设(P, V)是某一语言L的交互式证明系统，P是证明者，V是验证者。称P是完全零知识，如果对于每个概率多项式时间的交互V，都存在一个概率多项式时间算法M（模拟器），使得L中的每个x都有：$(P,V)(x)$ 和$M(x)$同分布
    • V没有从P中获得任何知识，因为同样的输出也可以在没有访问P的情况下获得
    • 分布相同：perfect zero knowledge；计算上不可区分：computational zero knowledge

  • 图的同构的交互式证明（是一个NP问题）

    • 图$G_1=(V_1,E_1)$和图$G_2=(V_2,E_2)$是同构的，如果存在一对一的映射$\pi：V_1\rightarrow V_2$使得$(u,v)\in E_1,(\pi(u),\pi(v))\in E_2$

      image-20220402130807081

    • 定义语言GNI：$GNI=(G_1,G_2), G_1\ and\ G_2\ are\ non-isomorphic$

    • 如果两个图是非同构的，证明者可以凭此说服验证者（GNI的交互式证明如下）

      • 输入：$G_1=({1,…,n}, E_1)$和$G_2=({1,…,n},E_2)$
      • 验证者随机选择数字1或2，据此确定使用$G_1$或者$G_2$，并随机选择一个1到n的排列作为映射$\pi$，将图映射为新的图$H$，把$H$发给证明者，证明者发回和$H$同构的图序号1或者2——如果$G_1$和$G_2$确实不同构，则证明者一定可以知道到底哪个图才和$H$同构，因此证明者必须发回正确的序号才能让验证者接受
        • 完整性：如果两个图非同构，则验证者发送的图只能同构于其中一个，证明者总是能返回正确的答案
        • 可靠性：如果两个图同构，证明者只有一半的概率返回正确答案，重复此过程则可靠性更高

  • 图的三着色性的交互式证明

    • 形式化定义：$G=(V,E)$是三着色的，如果存在一个映射$\phi: V\rightarrow (1,2,3)$使得任意的$(u,v)\in E:\phi(u)\neq\phi(v)$

      image-20220402134441323

    • 输入：一个图，证明者可以用三个颜色给图的顶点着色

    • 证明者选择一个随机的颜色排列，将顶点的颜色放入信封发给验证者

    • 验证者收到后随机选择一个边，证明者揭示对应的节点颜色，若两个节点的颜色不同，验证者接受

    • 完整性：如果$G$是三着色的，则一定满足条件；可靠性：如果$G$不是三着色的，则至少有两个节点颜色一致，验证者选中相应边的概率为$1/|E|$，若重复多轮，则蒙混过关的概率会逐渐下降，最终低于1/3

      image-20220402135150949

  • 若两个零知识证明系统串联，则最终的交互过程仍然是零知识的；如果两个零知识证明系统并联，则不是零知识的，因为验证者可以通过让证明者相互竞争算力，选择计算量更大的证明者，获得知识

  • 所有NP问题都可以用于零知识证明

应用

  • Fiat-Shamir Identification

    • 前提：可信中心发布n，$n=pq$，p和q保密；A选择一个和n互质的素数s，计算$v=s^2\ mod\ n$，在可信中心注册v作为A的公钥
    • 过程：
      • A给B：$x=r^2\ mod\ n$
      • B给A：$e$，e为0或者e为1
      • A给B：$y=rs^e\ mod\ n$
      • B验证：$xv^e=y^2$

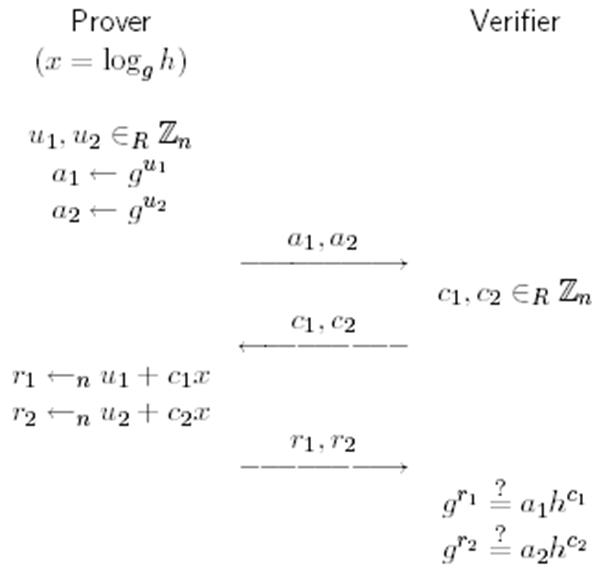
  • $\sum-protocol$ 重点（假设验证者是诚实的）

    • 定义：

      image-20220430133245428

    • 令$R={(v;w)}$为一个二元关系（v是证明者和验证者的公共输入statement，w是证明者的私有输入witness），此时给定一些多项式p，对于所有的元素都有$|w|\leq p(|v|)$

    • 令$L_R={v|\exist w:(v;w)\in R}$

      image-20220402143147394

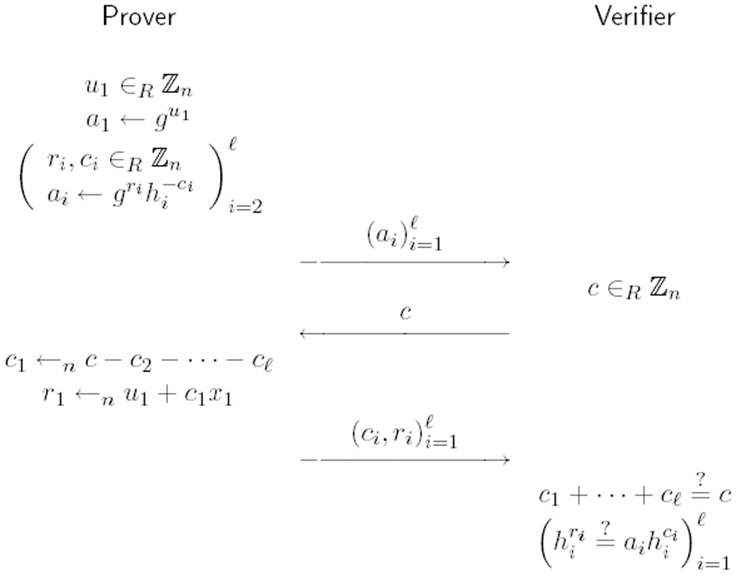
    • 关系R的$\sum-protocol$是一个证明者和一个验证者之间的协议，形式类似于上图，并满足：

      • 完整性：如果按协议执行，验证者接受（验证时等式成立）
      • 特殊的可靠性：对于任意的$v\in L_R$且任意一对$c\neq c’$的三元组$(a,c,r)$、$(a,c’,r’)$，可以很快计算出一个w，使得$(v;w)\in R$——证明者作弊成功的可能性最多为1/n，n为挑战空间的规模
      • 特殊的honest-verifier zero-knowledge：对于任意的$v\in L_R$，存在一个概率多项式时间算法，能够模拟出三元组$(a,c,r)$，其概率分布和诚实参与者交互结果的概率分布相同——对于诚实的验证者才是零知识的（证明此性质，需要去掉证明者端，验证者随机生成c和s，根据v、c、r构造a，使得验证的等式成立）

    • Schnorr’s protocol 和 Okamoto’s protocol 都是特殊的honest-verifier zero-knowledge（证明略）

  • 并联的$\sum-protocol$（基础的$\sum-protocol$为Schnorr’s protocol，见上一个blog）

    image-20220402145514025 image-20220402151407965

  • AND-Composition of sigma protocol：二者要使用一个公共的challenge（即图中的c）！

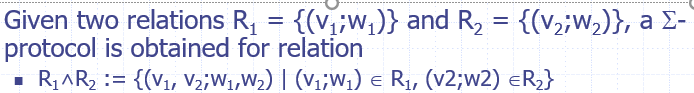
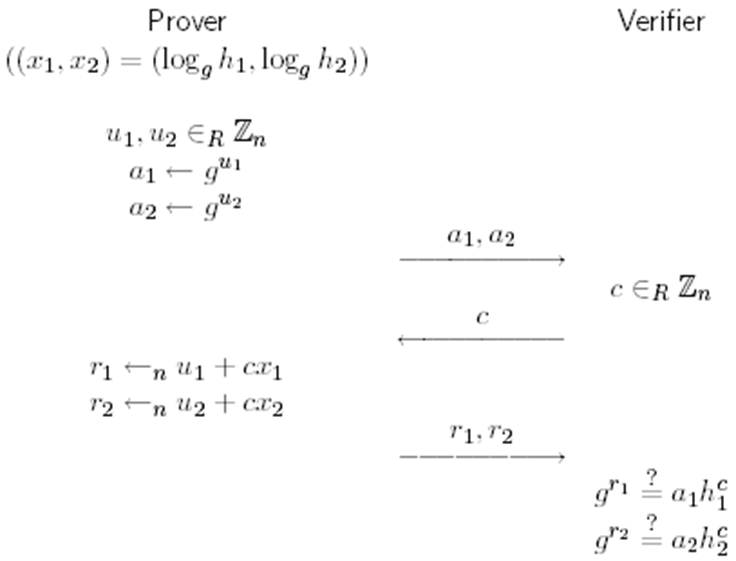
    image-20220402152414570 image-20220402152436926

  • EQ-Composition of sigma protocol

    • 特殊的AND composition：证明者使用相同的w，即${(v_1,v_2;w)|(v_1;w)\in R, (v_2;w)\in R}$

    • 使用相同的random tape $s_p$

      image-20220402161100742

      • 完整性：

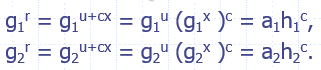
        image-20220402161138188

      • 特殊的可靠性：收到$(a_1,a_2,c,r)$和$(a_1,a_2,c’,r’)$，其中$c\neq c’$时，有下图的推理，因此可以得到$x=(r-r’)/(c-c’)$

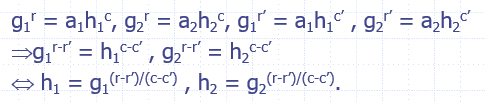
        image-20220402161253236

      • honest-verifier zero-knowledge：实际的、模拟的会话的分布一致，分别为

        image-20220402161524911

  • OR-Composition of sigma protocol：${(v_1,v_2;w_1,w_2|(v_1;w_1)\in R_1\vee (v_2;w_2)\in R_2)}$——验证者能确信证明者 知道其中一个秘密值，但无法确定证明者拥有的是哪个秘密值

    image-20220402162322095

  • 非交互性证明：证明者和验证者之间交互至多一次——证明者发送一条消息给验证者，即可使其相信证明者拥有某个知识

    • 任意实体都可以当验证者

    • 可以将任意的sigma protocol转为非交互的，记为sigma-proof

    • 以schnorr’s protocol为例（实现Schnorr signature 方案）：

      • 给定公钥h，知识为$x=log_gh$
      • 不再借助验证者“均匀采样以获得挑战c”，证明者直接计算a和消息m的哈希获得挑战c，即$c\leftarrow H(a,m)$
      • 具体算法（基于阶为n生成元为g的群和哈希算法H）：
        • 假设长为k的比特串，其中$2^k\leq n$
        • 密钥生成：生成公私钥对(h,x)，其中$h=g^x$
        • 签名生成：输入消息m和私钥x，选择$u\in_R Z_n$，设置$a\leftarrow g^u,c\leftarrow H(a,m),r\leftarrow_n u+xc$，消息m的签名为$(c,r)$
        • 签名验证：给定消息m、$(c,r)$和公钥h，若$c=H(g^rh^{-c},m)$成立则验证成功

    • 群签名：

      • 代表一个组的签名，该签名不会透露哪个用户实际产生了签名，但必要时仍然能够证明哪个组成员产生了给定的组签名

      • 组管理员$P_0$，组成员$P_l,l\geq 1$；密钥生成（一个公钥h，管理员以及各个成员的私钥$x_i$）、签名生成（给定消息m、公钥h和私钥$x_i$，输出一个签名s）、签名验证（给定消息m、公钥h、签名s，根据h决定s是否合法）、签名打开（给定消息m、公钥h、管理员私钥$x_0$、签名s，输出签名人的身份）

      • 除了组管理器以外，没人能够知道这些签名是否由同一组成员生成（称为不可链接性）

      • 具体算法

        • 密钥生成：所有成员选择自己的私钥$x_i\in_RZ_n$，公钥为$h=(g^{x_0},…,g^{x_l})$

        • 签名生成：$P_i$基于ElGamal加密，使用$h_0$计算$(a,b)=(g^r,h_0^rg^{x_i}),r\in_R Z_n$；给出下面关系的一个证明，作为非交互证明，表示$(a,b)$确实加密了$h_i$并且加密者知道私钥

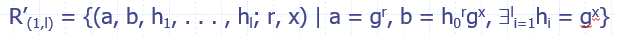
          image-20220402173757648 image-20220402174205761

        • 签名验证：类似于Schnorr signature

        • 签名打开：给定$(a,b)$，组管理员输出$d=a^{x_0}$，使用EQ-composition证明$log_ad=log_gh_0$，此时根据d，任何人都可以计算$b/d$，其结果就是产生此签名的成员的公钥

相关文章推荐