《密码协议》课程笔记(5) 门限密码协议
门限密码
- 动机:有时候,只有一方控制的访问是不可取的(密钥的所有权仅属于一方是不合理的),因此密钥的所有权需要分布给多方(群签名、给一个组织发消息)
- 门限密码:面向组的密码学,在多个参与方中分发密码。例如,10个人有数字签名私钥,但签名需要7人以上的参与——秘密共享方案是基础
秘密共享方案
将秘密分成多份,有足量的份数时,秘密可以被重建,否则不能重构秘密或其中任何部分——
(t,l)秘密分享方案将一个秘密分割为l份,至少t个才能重构,t称为断点(breaking point)类似多项式:多项式f的阶为
t-1,则需要t个多项式上的点才能确定f(0)一旦t个人通信,恶意内部人员可以获得密钥——需要一个能解密和签名但不泄露密钥的系统
(举了一个例子说明了)将一个比特串直接分成两块或更多块不是共享秘密的安全方法,并且不适用于长度为1的串
- 对于秘密比特$s$,选择一个随机的比特$r$,并设置shares $s_1=s\bigoplus r$,$s_2=r$,此时$s_1$和$s_2$不会泄露$s$,并且$s_1\bigoplus s_2=s$
- 如果$r$是均匀分布的,则$Pr(s_1=0)=Pr(r=s)=1/2$(r和s独立,并且r=1和r=0概率均为1/2),因此$s_1$和$s_2$都是均匀分布($s_2=r$)
- 进一步,可以随机选择$l-1$个比特$r_i$,计算$s_1=s\bigoplus r_1\bigoplus … \bigoplus r_{l-1},s_2=r_1,…,s_l=r_{l-1}$
具有参与者$P_1,…,P_l$的秘密共享方案包含:分发协议(一个协议使得deal D分享一个秘密s,每个参与者获得一个share $s_i$),重建协议(一个协议使得秘密s能够通过任何一组合格参与者的秘密片段恢复,这里参与者是$P_1,…,P_l$的子集)——所有这种子集构成的集合称为access structure
安全需求(满足安全需求的秘密共享方案称为perfect)
- 符合条件的参与者集可以通过shares确定s
- 不符合条件的参与者集都不能通过shares确定关于s的任何信息
(t,l)门限密码
access structure定义为:

shamir’s threshold scheme:
$F_p$为p阶有限域,$p>l$,分享的秘密$s\in Z_p$
秘密分发:分发者D选择一个$t$阶随机多项式$a(x)\in_R Z[x]$,$a(0)=s$,分发$s_i=a(i),i=1,..,n$
秘密重构:利用拉格朗日插值法恢复

是perfect的(少于t人参与重构时,任何$a(0)$都是可能的)
只能抵抗被动攻击(如果分发者发给参与者的碎片是不正确的,参与者无法察觉,并且如果重构时某个参与者唯一不用正确的碎片,他可以从其他参与者的正确碎片恢复秘密),安全性依赖于方案中各方诚实执行协议,诚实执行后不合格参与者不能推断出关于秘密的信息
抵御主动攻击的秘密共享方案——可验证的秘密共享(verifiable secret sharing, VSS)方案——抵御主动攻击:分发时,分发者向部分或全部参与者发送不正确的碎片,并且重构时,参与者提交不正确的碎片
Feldman’s VSS
shamir方案的推广;$p$为大素数,$
$为p阶循环群,$s\in Z_p$ 分发:
分发者选取一个多项式$a(x)=s+a_1x+…+a_{t-1}x^{t-1},a_j\in Z_p$,将$s_i=a(i)$分发给参与者,计算并广播承诺$B_j=g^{a_j},0\leq j<t$
参与者验证下式是否成立,以检查分发者是否诚实
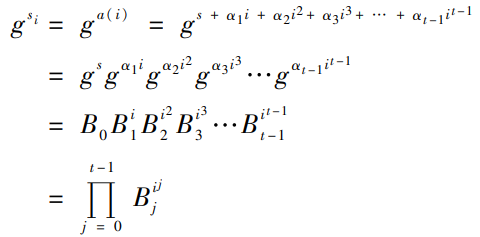
重建:执行shamir门限秘密分享方案即可;如果少于t个参与者能够重构原始秘密,意味着$s=log_gh$被求解,因此离散对数问题是困难的假设下,少于t个参与者不能计算秘密——计算安全
Pedersen‘s VSS
shamir+承诺,信息论安全(由于是Pederson commitment)
$
$为素数p阶循环群,h为群里的随机元素,因此没人知道离散对数$log_gh$ 分发:
- 分发者随机选择两个多项式:$a(x)=a_0+a_1x+…+a_{t-1}x^{t-1},a_j\in Z_p$和$b(x)=b_0+b_1x+…+b_{t-1}x^{t-1},b_j\in Z_p$,$a_0=s$,碎片$s_i=(a(i),b(i))$
- 分发者广播承诺值$C_j=g^{a_j}h^{b_j}$
重建:
参与者验证:
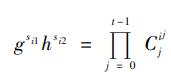
执行shamir门限秘密分享的重构算法,以恢复秘密
方案中,承诺与秘密相关的只有$C_0=g^sh^{b_0}$,而对任意的$\hat s\in Z_p$,都有唯一的$\hat b\in Z_p$使得$C_0=g^{\hat s}h^{\hat b}$,因此$C_0$没有泄露s的任何信息
如果分发者知道$log_gh$,则可以作弊

