More Than Code

B树，B+树

发表于 分类于
本文字数： 4.1k 阅读时长 ≈ 4 分钟

数据库索引BTree和B+Tree

BTree

  • 大多平衡查找树（Self-balancing search trees）如AVL树、红黑树，都假设数据放在内存。B树的使用是为了减少以块的形式读取磁盘数据时，访问磁盘的I/O次数
    • 平衡树的操作（增删改查、最大最小值）需要$O(h)$次访问，$h$ 是树高，一般是$logn$，$n$为结点数
    • B树的高度，可以通过调整树结点包含的键（或者说数据库中的索引，一个位置信息）的数目控制。一般B树结点的键的数目和磁盘块大小一样
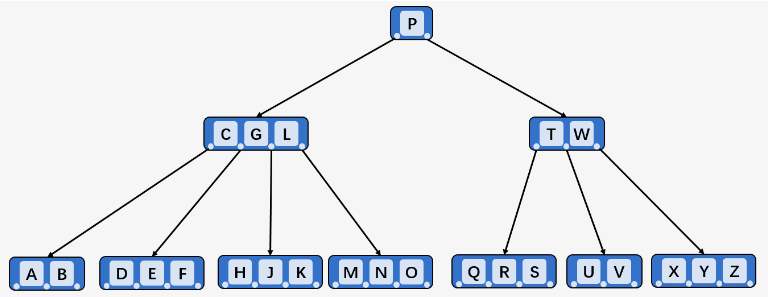
image-20220621150506198

特性：

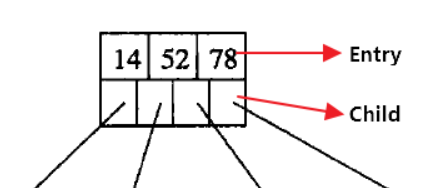
（可以参考上图，其中的字母就是Key）

  1. 所有叶子结点出现在同一层，不带信息，可以视为外部结点，指向这些结点的指针为空

  2. 每个结点包含的Key数目，由B树的最小度数$t$确定上界和下界，$t$取决于磁盘块的大小

    • 根结点至少有一个Key

    • 根结点以外的每个结点至少有$t-1$个key（有$t$个孩子），至多有$2t-1$个key

    • 有时的表述为$m$阶，则[m/2]-1 <= n <= m-1

  3. 包含$x$个key的结点有$x+1$个孩子

  4. 结点的key升序排列，两个key（$k_1,k_2$）之间的孩子结点的key在$(k_1,k_2)$之内

  5. B树的搜索从根结点开始，根据结点的孩子树做多路分支选择，每次判断进行一次磁盘I/O操作

  6. B树查找、插入和删除操作的时间复杂度为$O(logn)$

查找

  • 二叉查找树类似，只是B树每个结点包含多个关键字

  • 若待查找的Key为k：（参考上图）

    • 从根结点开始递归向下查找
    • 如果结点包含键 k ，则返回结点指针
    • 如果不包含，则查找该结点的合适子结点，子结点Key均要小于等于 k
    • 抵达叶子结点且没有找到 k，返回null

  • B树节点的属性：

    1
    2
    3
    4
    5
    int *keys;  // 存储Key的数组
    int t;  // 最小度 (定义一个结点包含Key的个数 t-1 <= num <= 2t -1) 
    BTreeNode **C;  // 存储子结点指针的数组
    int n;  // 当前结点包含的关键字的个数
    bool leaf;  // 是否为叶子结点

中序遍历

和二叉树中序遍历相似，先递归遍历左边子结点，在遍历当前结点内容，最后遍历最右边子结点

插入

  • 插入Key k ，需要从根结点开始向下遍历直到叶子结点，判断插入k后是否超出结点本身最大可容纳的Key个数

  • 如果超出，则拆分一个结点的孩子，例如x结点的孩子结点被拆开，KeyI上移，以它对结点 y拆分，拆成包含Key [G、H] 的结点 y 和包含Key [J、K] 的结点 z .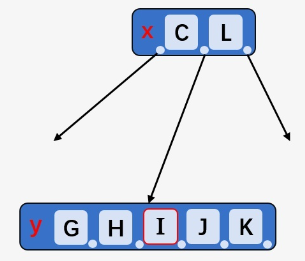

    image-20220621153756488

  • 具体插入关键字k的过程：

    1. 初始化 x 为根结点
    2. 当 x 不是叶子结点：
      • 找 x 下一个要访问的子结点 y
      • y 没有满，则结点 y 是新的 x
      • y 满了，拆分 y：
        • x 的指针指向结点 y 的两部分，第二部分拷贝t-1个y的Key
        • 如果 k 小于 y 中间的key， 将 y 的第一部分作为新的 x ，否则将 y 的第二部分作为新的 x
        • 将 y 的一个关键字上移到父结点 x 中
    3. x 是叶结点时，由于已经提前查分所有结点，x 必定至少有一个额外的Key空间，进行简单的插入

  • 为了避免回溯（可能父结点也满了，回溯会增加I/O次数），在插入新的Key前会将已满的结点提前拆分，但这可能带来很多不必要的拆分操作

  • 下图所示，插入I时，原来的CGL满了，拆分；又发现L的第一个左子结点满了，又要进一步拆分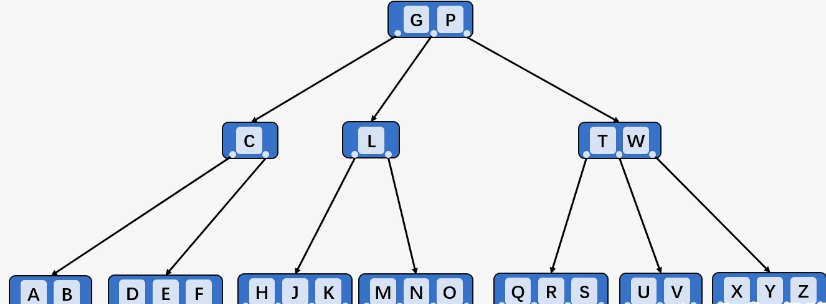

    image-20220621154319407 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 结点y已满，分裂结点y 
void BTreeNode::splitChild(int i, BTreeNode *y) { 
    // 创建一个新的结点存储 t - 1 个关键字
    BTreeNode *z = new BTreeNode(y->t, y->leaf); 
    z->n = t - 1; 

    // 将结点 y 的后 t -1 个关键字拷贝到 z 中
	for (int j = 0; j < t-1; j++) 
		z->keys[j] = y->keys[j+t]; 

	// 如果 y 不是叶子结点，拷贝 y 的后 t 个孩子结点到 z中
	if (y->leaf == false) { 
		for (int j = 0; j < t; j++) 
			z->C[j] = y->C[j+t];  
	}

	// 将 y 所包含的关键字的个数设置为 t -1——y 中包含的关键字变为 2t-1 - (t-1) -1 
    y->n = t - 1; 

	// 给当前结点的指针分配新的空间，父结点将多一个孩子
	for (int j = n; j >= i+1; j--) 
		C[j+1] = C[j]; 

	// 当前结点的下一个孩子设置为z 
	C[i+1] = z; 

	// 将所有父结点中比上移的关键字大的关键字后移，找到上移结点的关键字的位置
	for (int j = n-1; j >= i; j--) 
		keys[j+1] = keys[j]; 

	// 拷贝 y 的中间关键字到其父结点
    keys[i] = y->keys[t-1]; 

	// 当前结点包含的关键字个数加 1 
    n = n + 1; 
}

删除

  • 如果删除内部结点的Key，需要对结点的子结点重新排列

  • Keyk在叶结点x，删除即可

  • Keyk在内部结点x中：

    1. x中k之前的第一个子结点y至少有t个Key，则子结点y中找到k的前驱结点k_0，递归删除k_0，将x中的k替换为k_0（例如，删除G，此时删除F并把G替换为F）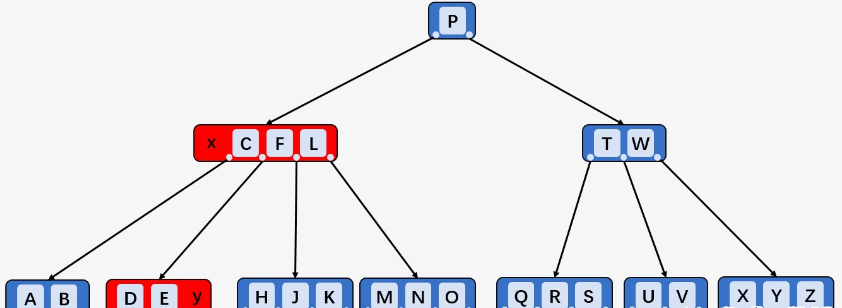

      image-20220621161225497

    2. x中k之前的第一个子结点y的Key少于t ，则检查结点x中k的后一个子结点``z 的Key数目，如果z至少有t个Key，则找k的直接后继k_0并删除，k替换为k_0（例如，删除 C， y只有2个Key，而度为3，C 的后一个子结点z包含[D、E、F] ，其直接后继为D，删除D 并将C替换为D`）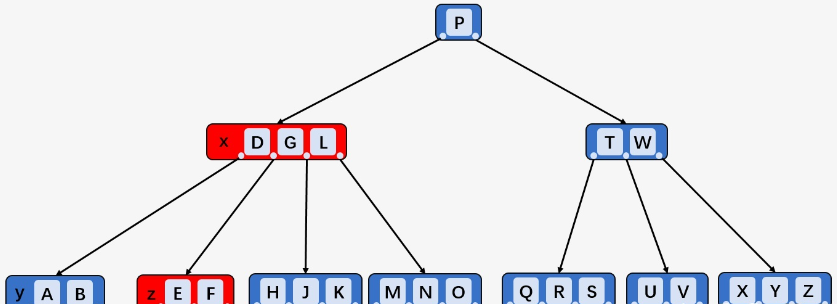

      image-20220621161842479

    3. y和z都只有t -1个Key，合并k和所有z的Key到y，x将失去k和子结点z，y此时包含2t -1个Key，释放z的空间并从y中递归地删除关键字k

  • 以上都假设结点富有，即结点删除这个key时，能根据自己所在的子树进行rebalance，不需要兄弟结点的帮助

  • 如果结点不富有：

    • 兄弟结点“富有”，从父节点要一个Key，兄弟结点补一个Key给父节点（例如，删除180，父节点的230下移，右兄弟结点[240,250,260]的240上移）

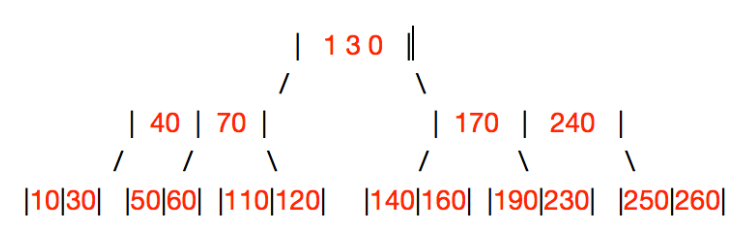
      image-20220621162734903image-20220621163325461

      image-20220621163325461

    • 兄弟结点不富有：

      • 父节点不富有：先从父节点要一个key，让父节点找“叔叔结点”、“爷爷结点”（例如，上图继续删除50，要下来父节点的40，兄弟合并）

        image-20220621163443195

      • 父节点富有：从父节点要一个下来，然后兄弟合并（例如，继续删除140）

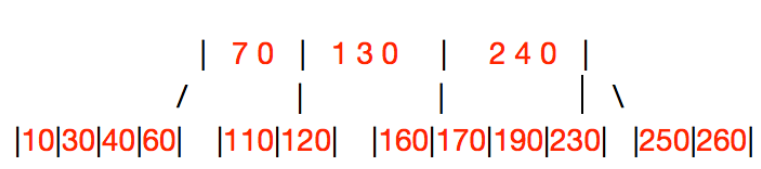
        image-20220621163559279

B+Tree

  • B树所有中间结点均存储数据指针（即指向了包含相应Value的磁盘文件块），B+树仅在叶子结点存储数据指针，因此所有数据地址必须要到叶子结点才能获取，每次数据查询的磁盘IO次数都一样

  • 特征：

    • 内部结点有k个Key，就会有k+1个子结点（下方第一个图为内部结点，第二个图为叶结点）

      image-20220621193914691

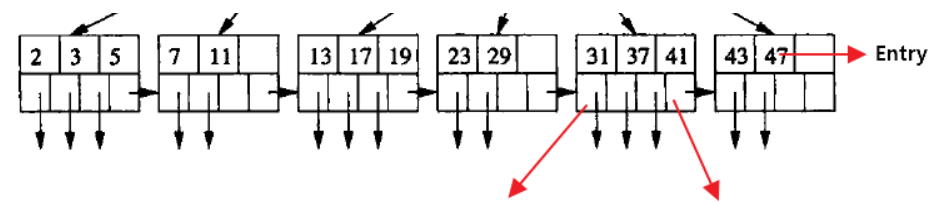
      image-20220621193951107

    • 每个元素不保存数据，只用来索引，所有数据都保存在叶结点

    • 所有的叶结点包含全部元素的信息，及指向含这些元素记录的指针，叶结点依Key升序链接

    • 所有中间结点元素同时存在于叶结点，在子结点元素中是最大（或最小）元素

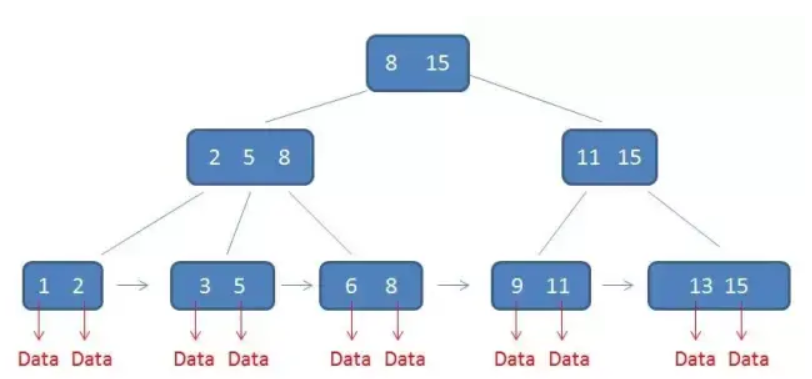
      image-20220621170620816

    • 数据库的聚集索引（Clustered Index）中，叶结点包含卫星数据。非聚集索引（NonClustered Index）中，叶结点带有指向卫星数据的指针。卫星数据指索引元素所指向的数据记录，如数据库某一行

  • 单行查询：例如查找元素3，自顶向下查询，第一次IO为[258]，第二次IO为35

  • 范围查询：例如查找3到11的范围数据。B树会自顶向下查询，查找到下限3，中序遍历到6，到8，到9，到11；B+树找到下限3时，直接通过链表指针遍历

插入

  • 插入全部在叶结点上进行，不能破坏Key的相对顺序
  • 结点中Key个数超过阶数，需要将结点 “分裂”
  • （下图B+树的阶数M=3，⌈M/2⌉=2、⌊M/2⌋=1）
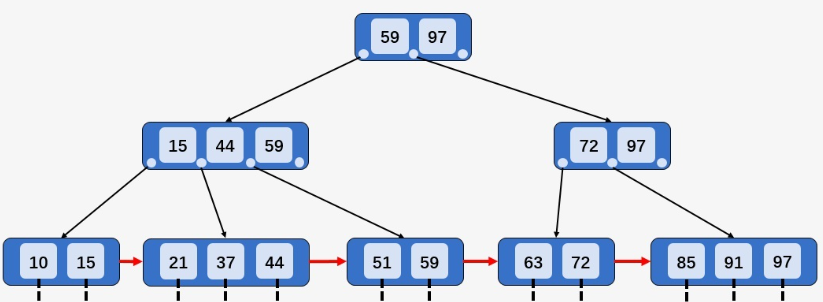
image-20220621171740365

  • 3种情况：

    1、被插入Key所在的结点，Key数目小于阶数，则直接插入（例如插入12 ，结点[10，15]有2个Key）

    2、被插入Key所在的结点，Key数目等于阶数，则将结点分裂为两个结点，分别包含⌊M/2⌋和⌈M/2⌉个Key，将⌈M/2⌉的Key关键字上移到双亲结点

    • 如果双亲结点的Key少于阶数，则插入操作完成（例如插入95，结点[85、91、97]的Key数目等于阶数，分裂为[85、91]和[97]，95插入[95、97] ，91上移至其双亲结点）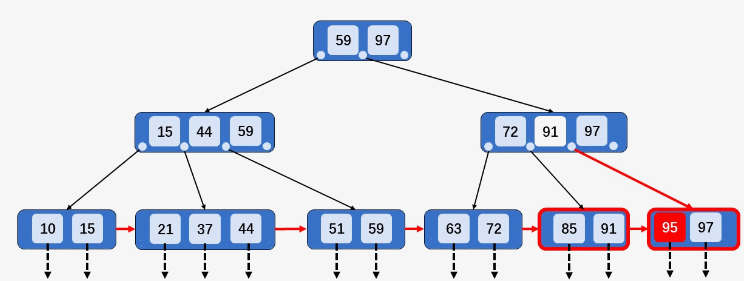

      image-20220621180358087

    • 如果双亲结点的Key等于阶数，则继续分裂双亲结点（例如插入40，37上移到父结点，父结点[15、37、44、59]的Key多于M，分裂父结点[15、37、44、59]为[15、37]和[44、59]，37上移到爷爷结点[37、59、97]）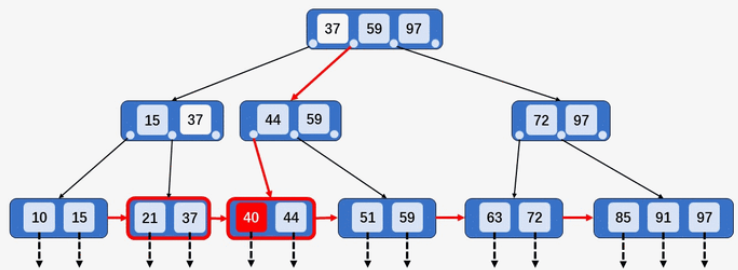

      image-20220621180519757

    3、被插入Key比当前结点的最大值还大，需要及时修正，再做其他操作（例如插入100，插入后根结点到该结点经过的所有结点的最后的值，都由97改为100，然后分裂）

删除

B+树中做删除Key的操作，采取如下的步骤：

  1. 删除该Key，如果不破坏 B+树本身的性质，直接完成删除操作（情况 1）
  2. 如果删除操作导致其该结点中最大（或最小）值改变，则相应改动其父结点中的索引值（情况 2）
  3. 在删除Key后，如果导致其结点中Key个数不足，可以向兄弟结点借，或者同兄弟结点合并（情况 3、4 和 5）

B+树在磁盘里的样子

  • user table：id为主键，每行数据为record，磁盘中被分为不同的数据页

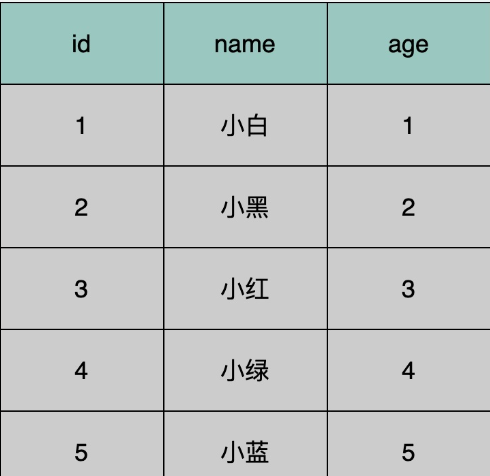
    image-20220621170325480
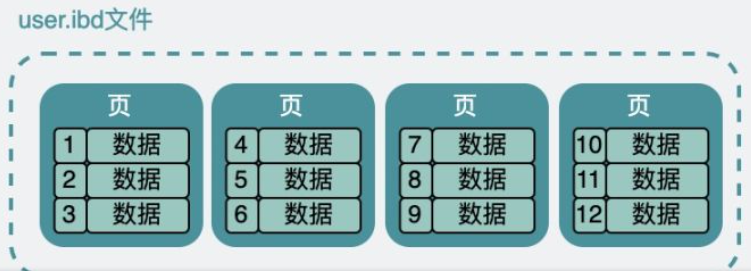
image-20220621180824413

  • 此时可以生成一个页目录，从而通过二分查找找到相应的页，再取出来判断record是否是客户端请求的record

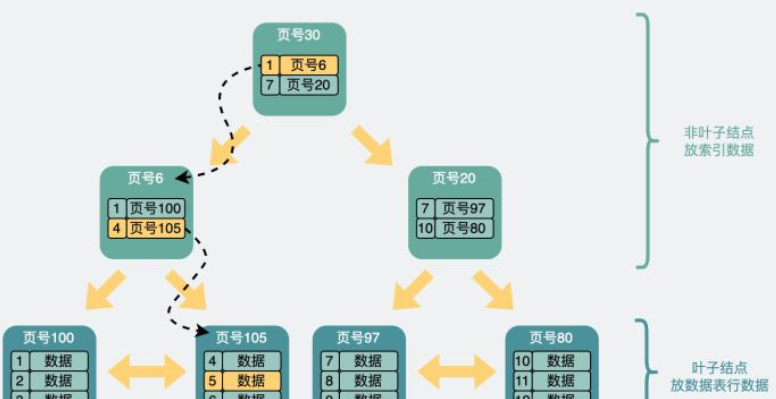
  • 为了加速搜索，每个页选出id最小的record，组成一个新的页（这个页的record中，只有主键id，以及所在页的页号），于是页之间有了层级关系，下图是两层B+树的结构

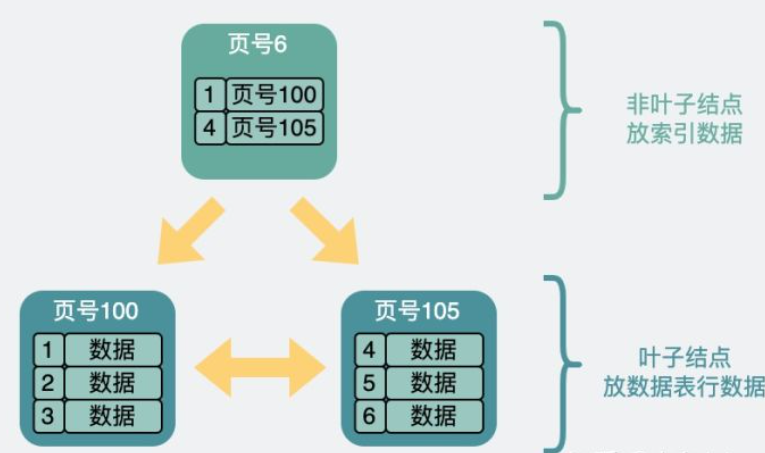
    image-20220621181044025

  • 三层结构查找id为5的record：从顶层页的record入手，其中record包含主键id和页号（页地址）。此时向左最小id为1，向右最小id为7，id=5的数据如果存在必定在左子结点，于是继续判断id=5>4，在右边的数据页里，加载105号数据页，从中找到id=5的实际record

    image-20220621181225717

参考资料

图解：什么是B树？（心中有 B 树，做人要虚心）一文读懂B-树

数据结构: B-Tree 的删除)

B+树看这一篇就够了（B+树查找、插入、删除全上）

什么是B+树？（详细图解）

相关文章推荐