Hands-on Machine Learning（4）

《Hands-on Machine Learning》第二部分阅读笔记（4）RNN 和 1D CNN 处理序列

使用 RNN 和 CNN 处理序列

循环神经元和层

最简单的 RNN：由一个神经元接收输入，产生一个输出，并将输出发送回自己
- 在每个时间步t（称为一个帧），循环神经元接收输入x[t]以及它自己的前一时间步长y[t - 1]的输出
- 可用时间轴来表示这个微小的网络
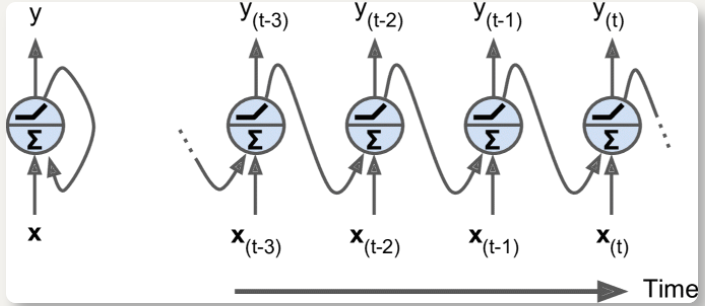
循环神经元层：在每个时间步t，每个神经元都接收输入向量x[t]和前一个时间步y[t - 1]的输出向量；此时输入和输出都是向量（当只有一个神经元时，输出是一个标量）
- 两组权重：
  - 用于输入x[t]——w[x]
  - 用于前一时间步长y[t - 1]的输出——w[y]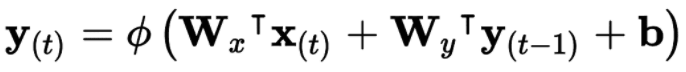
- 将所有输入和时间步t放到输入矩阵X[t]，一次计算出整个 batch 的输出

记忆单元

保留一些跨越时间步长的状态，称为记忆单元
单个循环神经元或循环神经元层是非常基本的单元，只能学习短期规律，通常是 10 个时间步
时间步t的单元状态，记为h[t]，是该时间步的某些输入和前一时间步状态的函数

输入和输出序列

可以同时输入序列并输出序列
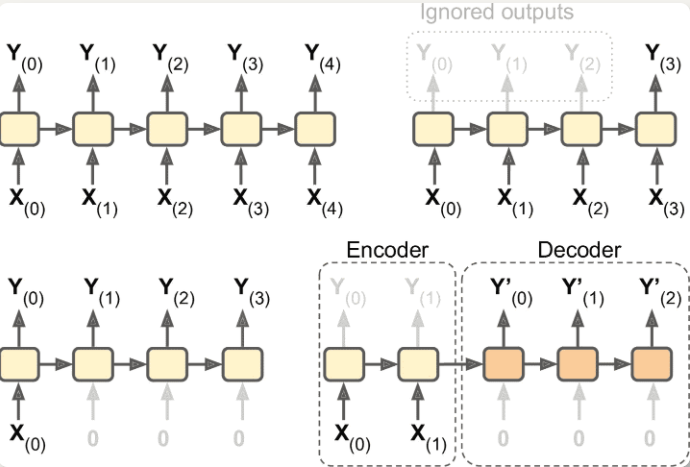
可以向网络输入一个序列，忽略除最后一项之外的所有输出——序列到向量；例如输入评论单词序列，输出情感评分
可以向网络重复输入相同的向量，输出一个序列——向量到序列；例如输入图像（或 CNN 输出），输出该图像标题
序列到向量 + 向量到序列：编码解码器；比用单个序列到序列的 RNN 实时地进行翻译要好得多，因为句子的最后一个单词可以影响翻译的第一句话

训练RNN

在时间上展开，然后反向传播（BPTT）
展开的网络先有正向传播，使用损失函数C(Y[0], Y[1], …Y[T]])评估输出序列（可能会忽略一些输出），梯度在损失函数所使用的所有输出中反向流动
如图，梯度流经损失函数使用的最后三个输出Y[2]，Y[3]和Y[4]，但不通过Y[0]和Y[1]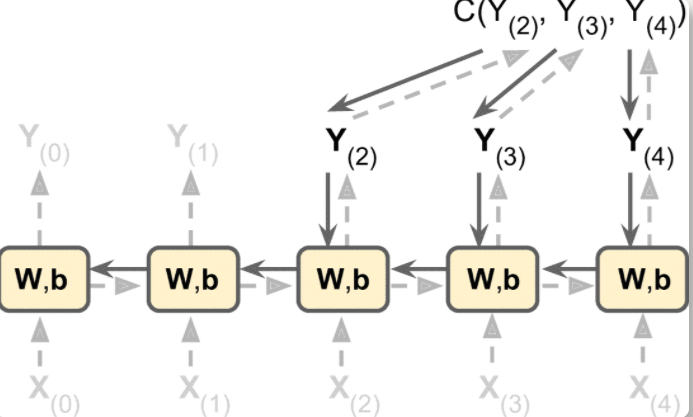

预测时间序列

generate_time_series()生成随机的时间序列，长度为n_steps，返回形状 [batch size, 时间步数, 1] 的 NumPy 数组

def generate_time_series(batch_size, n_steps):
    freq1, freq2, offsets1, offsets2 = np.random.rand(4, batch_size, 1)
    time = np.linspace(0, 1, n_steps)
    series = 0.5 * np.sin((time - offsets1) * (freq1 * 10 + 10))  #   wave 1
    series += 0.2 * np.sin((time - offsets2) * (freq2 * 20 + 20)) # + wave 2
    series += 0.1 * (np.random.rand(batch_size, n_steps) - 0.5)   # + noise
    return series[..., np.newaxis].astype(np.float32) 
    
n_steps = 50
series = generate_time_series(10000, n_steps + 1)
X_train, y_train = series[:7000, :n_steps], series[:7000, -1]
X_valid, y_valid = series[7000:9000, :n_steps], series[7000:9000, -1]
X_test, y_test = series[9000:, :n_steps], series[9000:, -1]

输入特征通常用 3D 数组来表示，其形状是[批次大小, 时间步数, 维度]，对于单变量时间序列，其维度是 1，多变量时间序列的维度是其维度数

基线指标（Baseline metrics）

使用 RNN 最好有基线指标：朴素预测（预测每个序列的最后一个值），或使用全连接网络

model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[50, 1]),
    keras.layers.Dense(1)
])

MSE 损失、Adam 优化器、 20 个周期

简单 RNN 实现

1
2
3

model = keras.models.Sequential([
  keras.layers.SimpleRNN(1, input_shape=[None, 1])
])

默认时，Keras 循环层只返回最后一个输出。要返回每个时间步的输出，必须设置return_sequences=True

循环神经网络可以处理任意的时间步，所以第一个输入维度设为None
SimpleRNN默认使用双曲正切函数激活
初始状态h[init]为 0，和时间序列的第一个值x[0]传递给神经元。神经元计算两个值的加权和，使用双曲正切激活，得到y[0]。简单 RNN 中，这个输出也是新状态h[0]。新状态和下一个输入值x[1]按此流程重复，直到输出最后一个值y[49]

某些模型需要先移出趋势和季节性，例如，研究网站的活跃用户数，它每月会增长 10%，需要去掉这个趋势。训练好模型之后可以将趋势加回，做最终预测

深度 RNN

将多个层堆叠

model = keras.models.Sequential([
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.SimpleRNN(20, return_sequences=True),
    keras.layers.SimpleRNN(1)
])

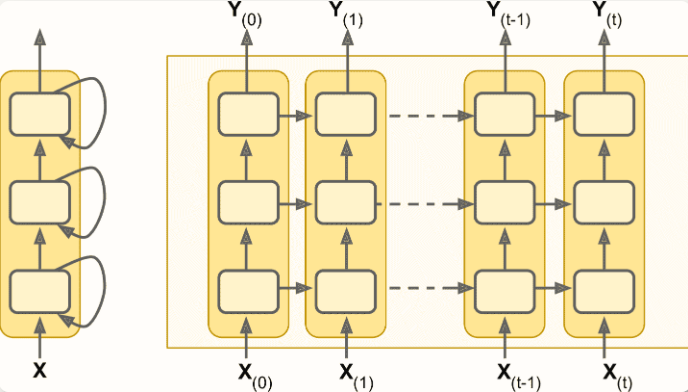
所有循环层一定要设置return_sequences=True，否则输出的是 2D 数组，即只有最终时间步的输出

优化：一个神经元表示隐藏态只有一个值。RNN 大部分使用其他循环层的隐藏态的所有信息

model = keras.models.Sequential([
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.SimpleRNN(20),
    keras.layers.Dense(1)
])

预测多个时间步

使用训练好的模型预测出下一个值，将这个值添加到输入中再预测下一个值——错误可能会累积

series = generate_time_series(1, n_steps + 10)
X_new, Y_new = series[:, :n_steps], series[:, n_steps:]
X = X_new
for step_ahead in range(10):
    y_pred_one = model.predict(X[:, step_ahead:])[:, np.newaxis, :]
    X = np.concatenate([X, y_pred_one], axis=1)

Y_pred = X[:, n_steps:]

一次预测10个值

修改输入向量，每个时间步有 10 个值

series = generate_time_series(10000, n_steps + 10)
X_train, Y_train = series[:7000, :n_steps], series[:7000, -10:, 0]
X_valid, Y_valid = series[7000:9000, :n_steps], series[7000:9000, -10:, 0]
X_test, Y_test = series[9000:, :n_steps], series[9000:, -10:, 0]

修改输出层

model = keras.models.Sequential([
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.SimpleRNN(20),
    keras.layers.Dense(10)
])
Y_pred = model.predict(X_new)

优化：之前是最后一个时间步预测 10 个值，可以在每个时间步预测接下来的 10 个值——时间步 0，模型输出一个包含时间步 1 到 10 的预测向量，在时间步 1，模型输出一个包含时间步 2 到 11 的预测向量，以此类推

# 目标序列，目标要包含出现在输入中的值（X_train 和 Y_train有许多重复）
Y = np.empty((10000, n_steps, 10)) # each target is a sequence of 10D vectors
for step_ahead in range(1, 10 + 1):
    Y[:, :, step_ahead - 1] = series[:, step_ahead:step_ahead + n_steps, 0]
Y_train = Y[:7000]
Y_valid = Y[7000:9000]
Y_test = Y[9000:]

model = keras.models.Sequential([
    keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.SimpleRNN(20, return_sequences=True),
    keras.layers.TimeDistributed(keras.layers.Dense(10))
])

def last_time_step_mse(Y_true, Y_pred):
    return keras.metrics.mean_squared_error(Y_true[:, -1], Y_pred[:, -1])

optimizer = keras.optimizers.Adam(lr=0.01)
model.compile(loss="mse", optimizer=optimizer, metrics=[last_time_step_mse])

必须在每个时间步添加全连接输出层，因此使用TimeDistributed层：将任意层（比如，紧密层）包装，在输入序列的每个时间步上使用，即输入从[批次大小, 时间步数, 输入维度]变形为[批次大小 × 时间步数, 输入维度]，运行全连接层，将输出从[批次大小 × 时间步数, 输出维度]变形为[批次大小, 时间步数, 输出维度]
此例子中，输入维度为 20，因为 SimpleRNN 维度为 20；输出为 10，因为包装的全连接层维度为 10
预测和评估时，只需最后时间步的输出，需要自定义指标

处理长序列

不稳定梯度

运行许多时间步，则展开的 RNN 是一个很深的网络
不能在时间步骤之间使用 BN，只能在循环层之间使用

层归一化：不在批次维度上做归一化，在特征维度上归一化；通常用在输入和隐藏态的线型组合之后

class LNSimpleRNNCell(keras.layers.Layer):
    def __init__(self, units, activation="tanh", **kwargs):
        super().__init__(**kwargs)
        self.state_size = units
        self.output_size = units
        self.simple_rnn_cell = keras.layers.SimpleRNNCell(units,
                                                          activation=None)
        self.layer_norm = keras.layers.LayerNormalization()
        self.activation = keras.activations.get(activation)
    def call(self, inputs, states):
        outputs, new_states = self.simple_rnn_cell(inputs, states)
        norm_outputs = self.activation(self.layer_norm(outputs))
        return norm_outputs, [norm_outputs]

call()接收：当前时间步的inputs和上一时间步的隐藏states；call()先使用简单 RNN 单元，计算当前输入和上一隐藏态的线性组合，之后归一化，激活，返回输出和新的隐藏态

构造器创建LayerNormalization层

model = keras.models.Sequential([
    keras.layers.RNN(LNSimpleRNNCell(20), return_sequences=True,
                     input_shape=[None, 1]),
    keras.layers.RNN(LNSimpleRNNCell(20), return_sequences=True),
    keras.layers.TimeDistributed(keras.layers.Dense(10))
])

短期记忆问题

数据在 RNN 中流动时会经历转换，每个时间步都损失了一定信息，一定时间后，第一个输入会在 RNN 的状态中消失

LSTM

设置 LSTM 层

model = keras.models.Sequential([
    keras.layers.LSTM(20, return_sequences=True, input_shape=[None, 1]),
    keras.layers.LSTM(20, return_sequences=True),
    keras.layers.TimeDistributed(keras.layers.Dense(10))
])

设置 LSTMCell 参数（此方法使用较少，因为RNN大多用来自定义层）

model = keras.models.Sequential([
    keras.layers.RNN(keras.layers.LSTMCell(20), return_sequences=True,
                     input_shape=[None, 1]),
    keras.layers.RNN(keras.layers.LSTMCell(20), return_sequences=True),
    keras.layers.TimeDistributed(keras.layers.Dense(10))
])

LSTM 单元：状态分为两个向量h[t]（短期记忆状态）与c[t]（长期记忆状态）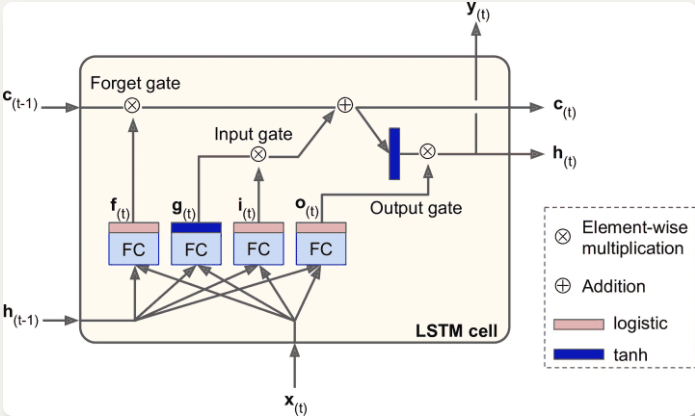
* 长期状态`c[t-1]`从左向右传播，先经过遗忘门丢弃一些记忆，后通过添加操作增加一些记忆（从输入门中选择一些记忆） * 长期状态复制后经过 tanh 激活，被输出门过滤，得到短期状态`h[t]` * 输入向量`x[t]`和前一时刻的短期状态`h[t-1]`传给四个不同的全连接层 * 输出`g[t]`的层是主要层，分析当前的输入`x[t]`和前一时刻的短时状态`h[t-1]` * 其它三个全连接层是门控制器，采用 Logistic 作为激活函数，输出范围在 0 到 1 之间，提供逐元素乘法操作 * 遗忘门（`f[t]`控制）决定哪些长期记忆需要被删除 * 输入门（`i[t]`控制）决定哪部分`g[t]`应该被添加到长期状态 * 输出门（`o[t]`控制）决定长期状态的哪些部分要读取和输出为`h[t]`和`y[t]` * 学习识别重要输入（输入门），存储进长期状态，并保存必要的记忆（遗忘门）
Keras 中，LSTM层基于keras.layers.LSTMCell单元
tf.keras.experimental.PeepholeLSTMCell支持窥孔——各个门控制器都可窥视长期状态，获取一些上下文信息

GRU

LSTM 的简化版本，实现同样的性能
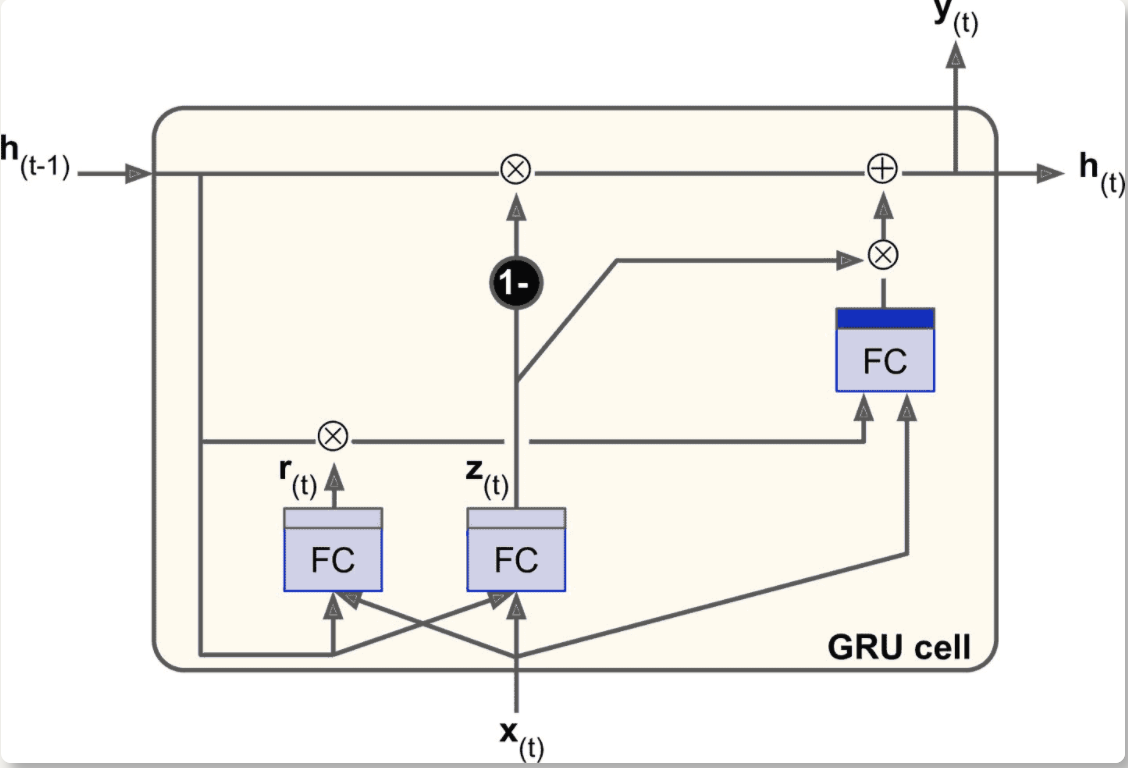
- 长期状态和短期状态合并为一个向量h[t]
- 一个门控制器z[t]控制遗忘门和输入门，输出 1 则遗忘门打开输入门关闭
- 取消了输出门，每个时间步输出全态向量
- 增加一个控制门r[t]控制前一状态的哪些部分呈现给主层g[t]
Keras 提供keras.layers.GRU层（基于keras.layers.GRUCell记忆单元）；只需将SimpleRNN或LSTM替换为GRU

一维卷积层

1D 卷积层在序列上滑动卷积核，每个核产生一个 1D 特征映射，学到一个非常短序列模式——用 10 个核，则输出会包括 10 个 1 维的序列（长度相同）
如果 1D 卷积层的步长是 1，填充为 same，则输出序列的长度和输入序列相同

通过缩短序列，卷积层可以帮助 GRU 检测长模式

model = keras.models.Sequential([
    keras.layers.Conv1D(filters=20, kernel_size=4, strides=2, padding="valid",
                        input_shape=[None, 1]),
    keras.layers.GRU(20, return_sequences=True),
    keras.layers.GRU(20, return_sequences=True),
    keras.layers.TimeDistributed(keras.layers.Dense(10))
])

model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse])
history = model.fit(X_train, Y_train[:, 3::2], epochs=20,
                    validation_data=(X_valid, Y_valid[:, 3::2]))

核大小比步长大，则所有输入会被用来计算输出
必须裁剪Y_train中的前三个时间步，因为核大小是 4，卷积层的第一个输出基于输入时间步 0 到 3；并用因子 2 对Y_train做降采样