More Than Code

Modeling the adversary to evaluate password strength with limited samples

发表于 分类于
本文字数： 3k 阅读时长 ≈ 3 分钟

《Modeling the adversary to evaluate password strength with limited samples》论文阅读笔记

摘要

  • 提供一种改进的方法，评估密码合生成策略的安全性
  • 设计一个猜测次数计算框架；提出对 PCFG 语法的几个改进；使用框架来研究各种策略下密码的猜测性

介绍

  • 密码合成策略的目的是让密码更难猜测，但并不清楚这些策略在保护用户方面有多有效——这是论文背后的动机，改进现有的评估密码组合策略强度的度量标准

  • 威胁模型（本文对攻击者的一些假设）：

    • 攻击者能进行$10^{12}$以上的猜测
    • 攻击者的知识仅限于密码数据集、目标密码组成策略、字典，并且这些数据量不会太大
    • 本文不关注”在线攻击“

  • 课题陈述：

    Our automated approach to evaluating password-composition policies can model a more efficient and more powerful adversary than previous machine-learning approaches, assuming an offline-attack threat model.

    • 大量借鉴了 Weir 等人的工作
    • 使用机器学习方法自动学习密码模板
    • 可以破解比以前的 PCFG 更多的密码
    • 贡献：
      • 开发了一个系统，基于可配置的混合训练数据自动学习密码猜测模型（PCFG），并将该模型应用于明文测试集，并以一种比显式枚举单个猜测快得多的方式来评估密码
      • 对 PCFG 进行改进
      • 提供了四个评估策略的应用案例

获得猜测次数

  • 提供一种比以前的机器学习方法更好的密码强度度量

  • Simple guess 算法

    • 给定训练密码 P 和测试密码 T，输出 T 中密码需要的猜测次数。辅助结构：哈希表 FREQ、哈希表 TEST

    • 步骤：

      • FREQ 建立 P 的密码字典，键为密码，值为出现次数；TEST 建立 T 的密码字典，内容同上
      • 新建一个列表 SORTEDGUESS，包含 FREQ 的每一项，按频率降序排列
      • 对 SORTEDGUESS 按序编号，第一个编号为1，第二个编号为2，以此类推；此时具体频率可以丢弃
      • 按序遍历 SORTEDGUESS，对每一项(p, g)，查看 TEST 中是否有密码 p，如果有，输出 TEST[p] 次的(p, g)，然后从 TEST 中删除相应键值对
      • 对 TEST 中剩余键值对(t, freq)，分别输出freq次的(t, -1)

    • 此算法中，猜测次数的临界值就是训练集中唯一密码数目

    • 可用于查看满足某一策略的密码集，其密码的猜测次数与猜中比例的曲线

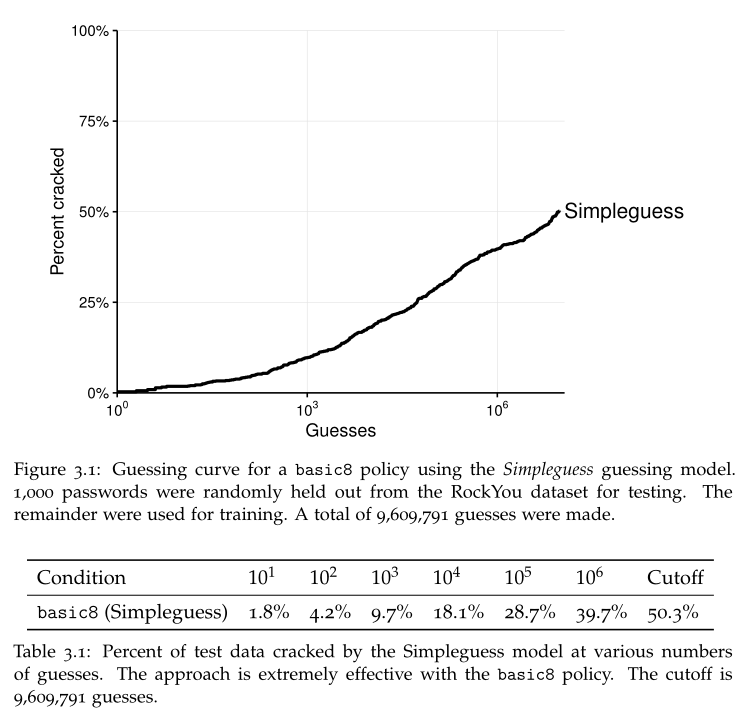
      image-20210721140836308

  • 与 PCFG 结合：将 PCFG 的输出作为 SORTEDGUESS，因为其输出本身是依据概率顺序递减

    • 过程如下：这里猜测密码的语法结构、数字串、特殊字符串来自训练密码，字母串可以来自训练密码也可以来自额外的wordlist

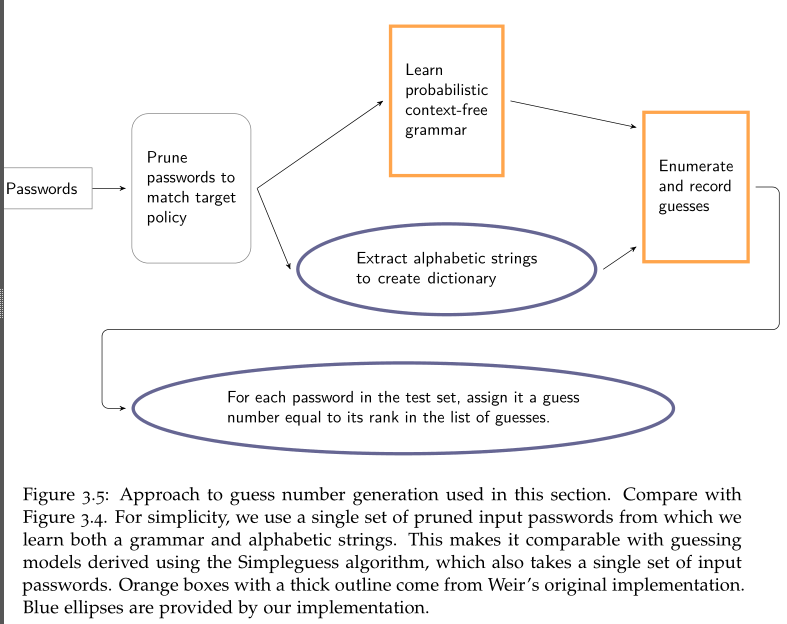
      image-20210721161237619

    • 改进：以上的方法，需要明确枚举猜测数据，限制了可以分配的猜测数字。具体改进后的流程如下（蓝色的框是对 PCFG 本身的改进）：

      • 可以为终端设置单独的语料库，而不是全都从训练数据中学习
      • 对不同来源的语料库进行加权：各个语料库建立密码字典，相应密码频率同语料库本身权重相乘，得到一个新的语料库。最终所有加权后的语料库，在运行时会得到一个新的”运行语料库“
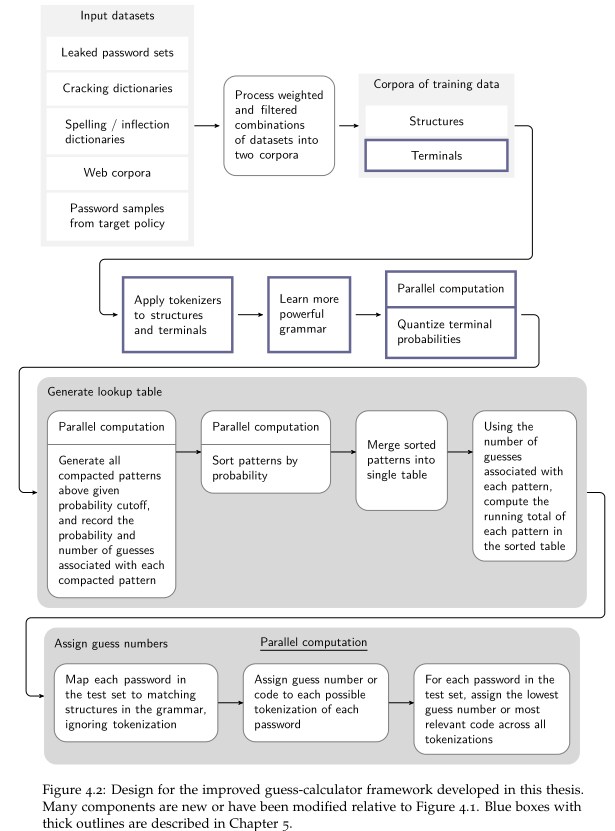
      image-20210721155326858

      • 查找表生成：提供一种以概率顺序存储大量密码的数据结构

        • 不再生成一个个的猜测密码，而是生成密码模板（一个模板对应多个猜测，每个猜测概率相同），并保存模板概率、猜测次数

        • 对所有模板排序，编号。第一个模板为1，第二个模板为1+a（a是第一个模板的猜测次数），第三个模板为1+a+b（b为第二个模板猜测次数），以此类推

        • 将同一个非终端下不同终端依据概率分割，概率相同的分作一组，即为一个”模板“

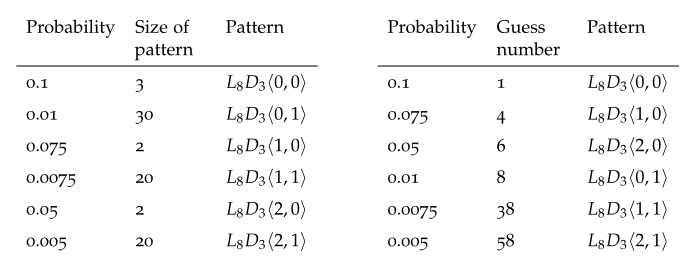
          image-20210722101030136

      • Intelligent skipping

PCFG的改进

学习字符串频率

  • 09年Weir提出的模型没有从训练数据中学习字母串的概率，而是为所有字母终端分配相同的概率

    image-20210718174533243

生成未知的终端字符串

  • 添加一个特殊的符号表示一组未知的终端，即添加了平滑技术
  • 假如样本 s 是以前没有看到的终端，则 s 被称为 singleton
  • 利用现有的 singleton 数目，估计遇到新的 singleton 的概率——如果总样本中有 10% 是 singleton，则估计遇见新 singleton 的概率为 10%，则未知终端的总概率为 10%，并假设所有未知终端的概率为 10%
  • 依据上述方法平滑概率

更复杂的PCFG结构

  • 方法1：{L，D，S}增加为{ {U，L}，D，S}，{U，L}代表大写字母和小写字母
    • 以小写形式存储终端，但以非终端形式记录它们的大小写
    • 即：如果遇到 Password、password、passWord，则认为遇到 password 三次，但三种不同的非终端分别遇到一次（PCFG需要分别记录非终端、终端的出现次数）
    • 本文认为，大小写在密码中主要用于满足密码设置要求，而不具有实际意义，因此上述的记录方式，能够让所有非终端都有机会尝试不同方式的大写，但本文没有对此做更多研究
  • 方法2：将出现比较多的结构本身，存储为一个非终端
    • 例如，遇到 password123! 时，为了保留“三个部分会同时出现”这一信息，需要将 password123! 单独作为一个终端存储，因此大幅扩展非终端集合${ {U,L}^i,D_i,S_i}$为${ {U,L,D,S}^i}$，此时上方终端将来自一个非终端 L8D3S1

语义分割（标记化）

  • 将原始字符串拆分为多个部分称为标记化

  • Weir 中非终端基于单个字符类指定，此时标记化为字符级别的标记化

  • Weir 的学习方式无法获得 token 之间的关联性

  • 方法1：

    • 一个简单方法是将整个密码作为单个 token 学习，例如对于 password123!，可以学习到$S\rightarrow(L8D3S1),(L8D3S1)\rightarrow password123!$
    • 此方法将完全无法生成没有见过的密码结构
    • 改进：同时学习标记化和未标记化的结构
      • 实验中，结果更偏向于未标记化的结构（即整个密码作为一个 token 学习），因为标记化的结构生成密码时，需要多个非终端连乘，得到的概率更低
      • 这使得生成密码与训练密码相似度更高

  • 方法2：

    • 基于语义的分割（标记化）
    • 例如，已知 n 元组“I love you”，则可在密码中识别“Iloveyou”并提取出来，形成结构 L1L4L3
    • 使用 Google Web Corpus 作为语义分割器（此数据集最长为 5 元组），需要将每个特殊符号、数字串分割开，以在字母串中寻找常用单词
    • 分割过程：
      • 根据语料，准备一个 trie 和一个 token table
      • 给定一个字符串 s，首先在 trie 中寻找 s 最长的前缀，在 token table 中查找此类前缀中最频繁的 token，以将前缀分解为单词。重复此过程
      • trie 与 token table 的建立：
        • token table：从语料库中移除非字母的 ngram，忽略大小写；对每个 ngram 保存其完整版、添加空格版本以及语料库中的频率，最后依据频率排序
        • trie：使用 python 的库 marisa-trie 实现；给定任意字符串，在 trie 中快速寻找此字符串最长的前缀

  • 方法3：

    • 无监督的分割
    • p@ssw0rd、p@ssw0rd1等密码用以上方法无法正确分割
    • 借用了别人的算法并进行了改进，此算法能够在具有完整句子的语料库中搜索最可能的分段结果，以对输入进行分割（基于无监督学习算法来识别完整文本中的单词）
    • 此方法的相关代码本文作者没有公开
相关文章推荐