《自然语言处理入门》阅读笔记(2) 第三章+第四章
二元语法
- 语言模型:语言的数学抽象,模拟说话顺序——给定词语序列,预测下一个词语的后验概率
- 数据稀疏
- 计算代价大
马尔可夫链与二元语法
马尔可夫假设:假定时间线上有一串事件按顺序发生,每个事件的发生概率只取决于前一个事件
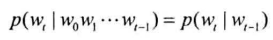
二元语法模型:
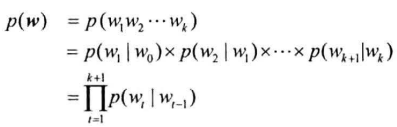
n元语法模型以此类推
n越大,数据稀疏问题越严重
平滑:将n元语法频次的折线平滑为曲线——线性插值法
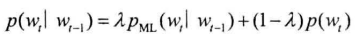
- $\lambda$:常数,平滑因子
中文分词语料库
- PKU:1998年《人民日报》语料库
- MSR:微软亚洲研究院语料库
- 繁体中文分词语料库
- 语料库的统计特征:词语种数、总词频
训练和预测分词
遍历一遍语料库即可,得到:

- @分隔开二元语法的两个单词
- 数字表明语法频次
- 特殊符号:始##始、末##末
对目标句子分词:以“商品和服务”为例
构建“词网“

词网的创建,是扫描出句子中所有的一元语法及其位置(与词典的全切分类似)
起始位置相同的单词写在一行
词网必须保证从起点出发的所有路径都将连通到终点,如果出现一元语法中没有的词语,则需要额外添加,以保证词网连通(如第五行”务“)
首行、末行对应:始##始、末##末
词网中的元素通过行号索引
词网中,第$i$行词语$w$与第$i+len(w)$行的所有词相连,都能构成二元语法,从而形成词图,词图从起点到终点的每一条路径都代表句子的一种分词方式,二元语法模型的解码任务是找到最合理的路径
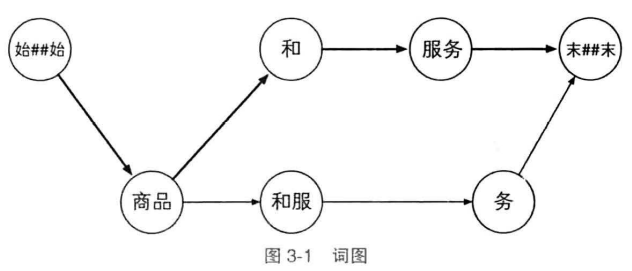
节点距离与最短路径
每条边的二元语法的概率作为距离——为防止下溢,将概率取负对数,浮点数乘法转为负对数加法
可使用拉普拉斯平滑
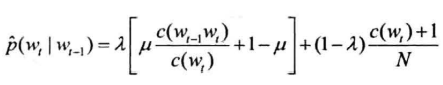
得到有向无环图
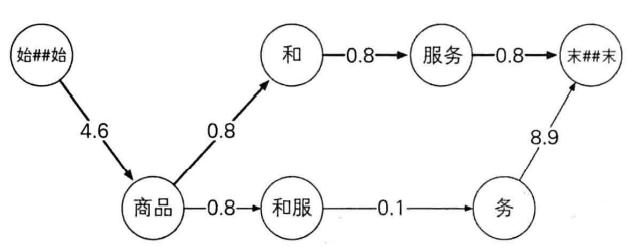
维特比算法计算最短路径,即为最佳分词方式
隐马尔可夫模型
序列标注问题
给定一个序列$x=x_1,…,x_n$,找出序列中每个元素对应的标签$y=y_1,…,y_n$
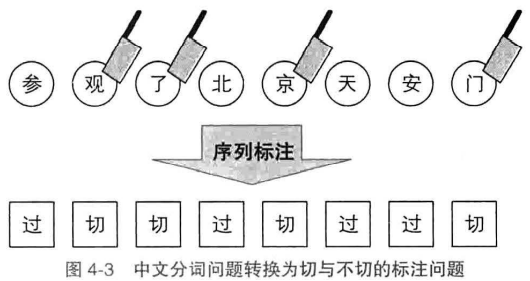
中文分词:
标注集为{切,过}
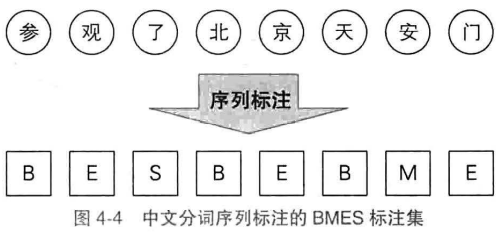
标注集为{B(词语首部),M(词中),E(词语尾部),S(单字成词)},最近的两个BE标签内所有字符合并为一个词,S对应的字符为单字词语
词性标注
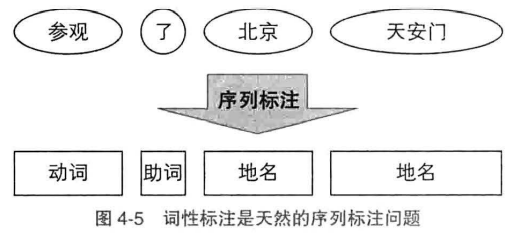
命名实体识别:将单词标注为”B/M/E/S-类别“,不构成命名实体的单词标注为O
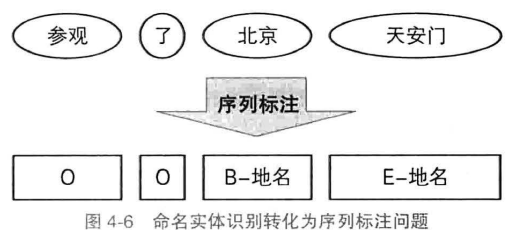
隐马尔可夫模型
隐马尔可夫模型描述两个时序序列联合分布$p(x,y)$的概率模型
- $x$序列外部可见,为观测序列
- $y$序列外部不可见,为状态序列
- 如观测$x$为单词,状态$y$为词性,需要根据单词序列猜测词性
- 三个要素:初始状态概率向量,状态转移概率矩阵,发射概率矩阵
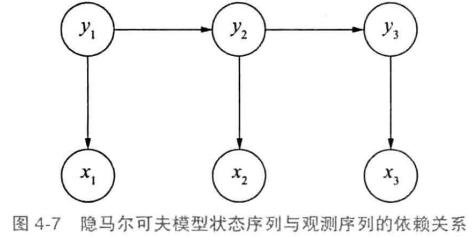
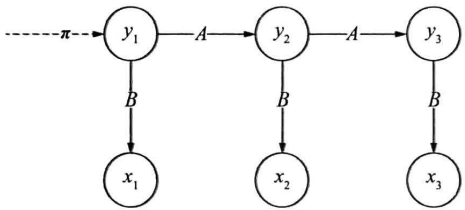
马尔可夫假设作用于状态序列,假设当前状态只依赖前一个状态,任意时刻的观测只依赖当前时刻的状态
初始状态概率向量:第一个状态$y_1$为初始状态,若有N种取值,则$y_1$为独立的离散随机变量,由初始状态概率向量$\pi$描述,给定其取值分布
状态转移概率矩阵:从$y_t$转移到$y_{t+1}$的概率(有N种状态,则有$N\times N$的方阵
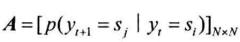
发射概率矩阵:给定状态$y_t$,$x$的概率分布参数向量。由于有N种状态,参数向量构成$N\times M$的矩阵
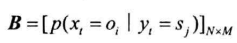
基本应用:
- 样本生成问题:给定模型$\lambda=(\pi,A,B)$,生成一系列的观测序列及其对应的状态序列
- 模型训练问题:给定训练集(一系列观测序列及状态序列),估计模型参数$\lambda=(\pi,A,B)$
- 序列预测问题:已知模型参数$\lambda=(\pi,A,B)$,给定观测序列$x$,求最可能的状态序列$y$
样本生成问题
例:医疗诊断
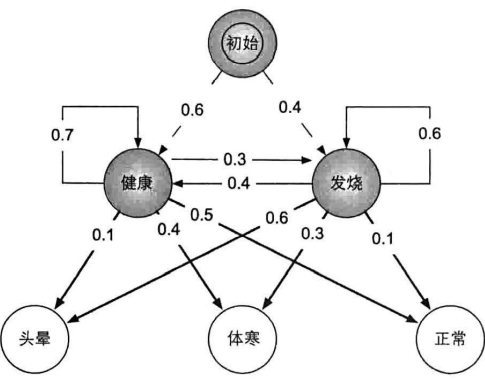
生成算法:长$T$的样本序列,其生成过程即为沿隐马尔可夫链生成$T$次
- 根据初始状态率向量采样第一个时刻的状态$y_1=s_i$
- 根据状态转移概率矩阵第$i$行采样下一时刻状态
- 对每个状态$y_t=s_i$,根据发射概率矩阵第$i$行采样$x_t$
- 重复2、3步骤$T-1$和$T$次,输出序列$x$、序列$y$
模型训练问题
根据训练集是否记录隐状态$y$,可分为完全数据(监督学习)和非完全数据(无监督学习)
下面均为监督学习,无监督学习使用EM算法
监督学习中,极大似然法来估计隐马尔可夫模型参数
估计转移概率矩阵
样本序列在时刻$t$处于状态$s_i$,下一时刻转移到状态$s_j$,统计此类转移频次,计入矩阵元素$A_{i,j}$,通过归一化估计$s_i$到$s_j$的转移概率
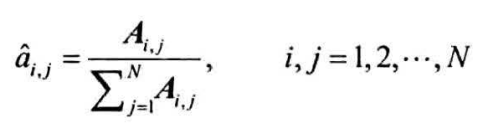
估计初始状态概率向量
可视为状态转移的特例,即从BOS转移到$y_1$,用类似的方法统计和归一化
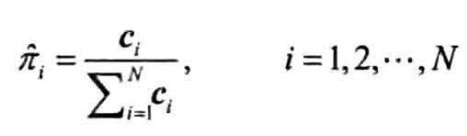
估计发射概率矩阵
统计样本中状态为$s_i$,观测为$o_j$的频次,进入矩阵元素$B_{i,j}$,则状态$s_i$发射观测$o_j$的概率为
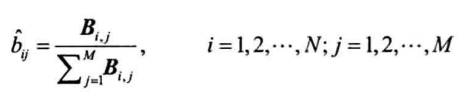
序列预测问题
给定观测序列,求最可能的序列及其概率
给定观测序列$x$和状态序列$y$,估计二者的联合概率$p(x,y)$
初始状态的概率由$\pi$决定:
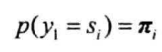
之后的状态由前一个状态转移而来,转移概率由$A$决定,因此状态序列的概率为:
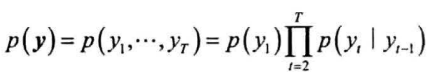
每一个状态都会发射一个观测,因此给定状态序列$y$,对应$x$的概率为:
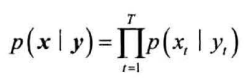
由此得联合概率:
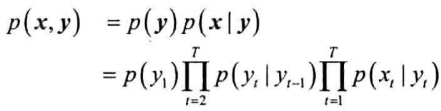
寻找最大概率对应的状态序列:
每个状态作为有向图的节点,节点距离由转移概率决定,节点本身花费由发射概率决定
所有备选状态构成有向无环图,所求状态序列即为最长路径
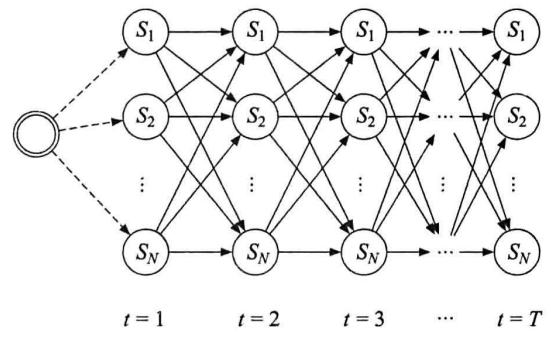
使用维特比算法搜索
从起点到时刻$t$的最优路径,对时刻$t$到$T$的路径选取也是最优
定义二维数组$\delta_{t,i}$表示时刻$t$以$s_i$结尾的所有局部路径最大概率
定义二维数组$\psi_{t,i}$,存储局部最优路径最后状态$y_t$的前一个状态
具体过程如下图所示:


