《自然语言处理入门》阅读笔记(3) 第五章+第六章
感知机
- 隐马尔可夫模型仅捕捉两个特征:前一个标签、当前字符
- 线性模型包括:提取特征的特征函数$\phi$、权重向量$w$
线性分类与感知机算法
线性模型:用一条线性直线或高位平面将数据一分为二,模型由特征函数$\phi$、权重向量$w$组成
特征向量:描述样本特征的向量
特征提取:构造特征向量的过程
分离超平面:任意维度空间中的线性决策边界
D维空间的超平面方程为:
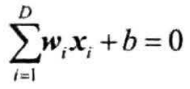
将$b$也看作一个权重,则:
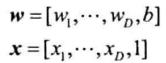
超平面方程简化为:
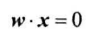
线性模型进行最终决策:
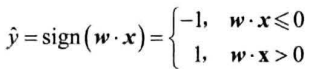
感知机算法:迭代式算法,每次读入一个样本,将预测结果与标签对比,计算误差、更新参数
过程:
- 读入训练样本$(x^{(i)},y^{(i)})$,预测$\hat{y}=sign(w\cdot x^{(i)})$
- 若$\hat{y}\neq y^{(i)}$,则更新参数$w \leftarrow w+y^{(i)}x^{(i)}$
如果数据本身线性不可分,则感知机的损失函数不收敛,此时解决方案为:
创造更多特征,将样本映射到高维空间,使其线性可分
使用其他训练算法,如支持向量机
使用投票感知机、平均感知机
投票感知机:每个epoch产生一个新模型,则预测时每个模型给出结果,结果根据模型在测试机上的准确率加权平均,作为最终结果
平均感知机:取多个模型权重的平均

模型调优方法:
- 特征工程(修改特征模板)
- 更换训练算法
- 收集、标注更多数据
结构化预测问题
- 预测对象结构的监督学习问题
- 例如:序列标注、语法分析、机器翻译
- 每个小部分都是分类问题,但必须考虑整体结构的合理性——由模型给出的分值或概率来衡量
- 给定模型$\lambda$、打分函数$score_\lambda(\cdot)$,利用打分函数给备选结构打分,选择分数最高的结构输出
结构化感知机
定义新的特征函数,将结构$y$也作为一种特征,得到结构化特征向量$\phi(x,y)$,则$score_\lambda(x, y)=w\cdot \phi(x,y)$,预测函数为:
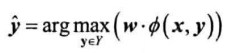
预测算法:

序列标注问题:
对连续标签提取转移特征:
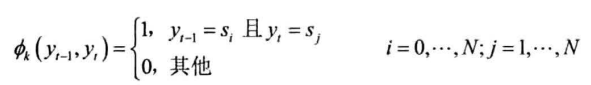
- $y_t$为序列第$t$个标签,$s_i$为标注集第$i$种标签,$N$为标注集大小,
获得每个时刻的状态特征:
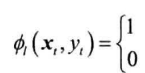
- 具体什么时候等于1,什么时候等于0,取决于特征模板
- 状态特征只与当前状态有关,与先前状态无关
结构化感知机的特征函数为转移特征、状态特征的合集:$\phi=[\phi_k;\phi_l]$,即$\phi(y_{t-1},y_t,x_t)$
整个序列的得分为各个时刻得分之和:
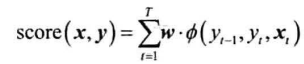
结构化感知机的维特比算法:
搜索分数最高的结构,这里即为对序列的搜索
定义$\delta_{t,i}$为时刻$t$以$s_i$结尾的所有局部路径最高分数
定义$\psi_{t,i}$存储局部最优路径中,最后一个状态$y_t$的前驱状态
具体如下:
初始化,$t=1$时初始最优路径的备选由$N$个状态组成,前驱为空
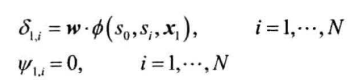
递推,$2\leq t$时每条备选路径增长一个单位,分数由打分函数确定。确定新的最优局部路径,更新以上两个二维数组
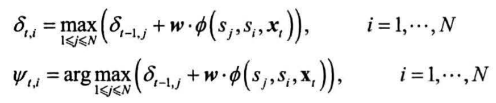
终止,获得最终时刻$\delta_{t,i}$数组中最大分数$S^*$与相应结尾状态下标$i_T^*$
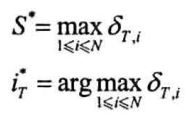
回溯,根据前驱数组$\psi$回溯前驱状态,获得最优路径下标$i^*=i_1^*,…,i_T^*$
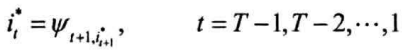
条件随机场
机器学习谱系
机器学习谱系图(忽略回归问题)
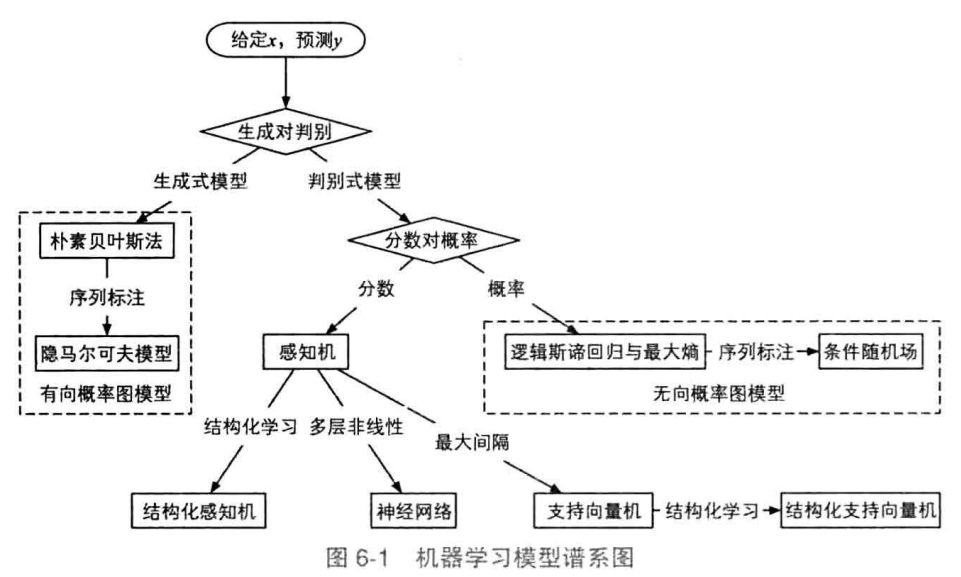
- 根本问题是,给定一些随机变量x,预测另一些随机变量y
- 根据y是独立变量还是多个关联的变量,分为分类问题和结构化预测问题
- 根据建模内容(联合概率分布$p(x,y)$还是条件概率分布$p(y|x)$),分为生成式模型和判别式模型
- 生成式模型:先有因素y,后有结果x——由联合分布模拟 $p(x,y)=p(y)p(x|y)$
- 如隐马尔可夫模型和朴素贝叶斯模型
- 间接建模$p(x)=\sum p(x,y)$
- 判别式模型:不关心x的内部联系,直接对$p(y|x)$建模
- 感知机、条件随机场、支持向量机、神经网络等
- 生成式模型:先有因素y,后有结果x——由联合分布模拟 $p(x,y)=p(y)p(x|y)$
概率图模型(PGM)
- 表示与推断联合分布$p(x,y)$
- 节点$V$表示随机变量,边$E$连接有关联的随机变量
有向图模型(DGM)
根据事件的先后因果顺序将节点连接为有向图
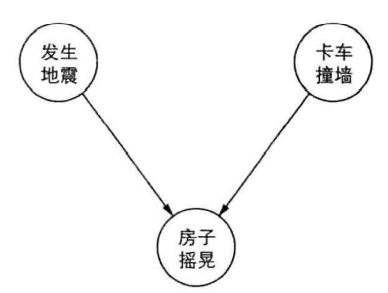
将概率有向图分解为条件概率的乘积,如果$\pi(v)$表明节点$v$的所有前驱节点,则联合分布$p(x,y)=\prod_{v\in V}p(x|\pi(v))$
无向图模型
不涉及条件概率分解,边代表两个事件有关联
将概率分解为所有最大团上的某个函数乘积:$p(x,y)=\frac{1}{Z}\prod_a{\psi_a(x_a,y_a)}$
- $a$为因子节点
- $\psi_a$为一个因子节点对应的函数,如$\psi_a(x_a,y_a)=exp{\sum_k w_{ak}f_{ak}(x_a,y_a)}$
- $k$为特征编号
- $f_{ak}()$为特征函数
- $w_{ak}$为特征权重
- $x_a,y_a$为与因子节点相连的所有变量节点
- 为约束上式成为概率分布,常数$Z$定义为归一化因子$Z=\sum_{x,y}\prod_a{\psi(x_a,y_a)}$
最大团:满足所有节点相互连接的最大子团
为便于分析,定义了一些虚拟的因子节点(factor),每个因子节点只连接部分节点,以组成较小的最大团
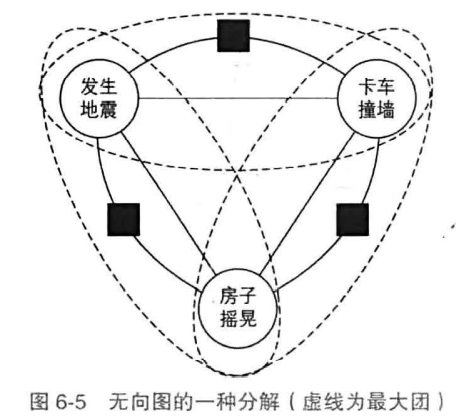
判别式模型常用无向图表示,归一化时对每个x求一个归一化因子$Z(x)=\sum_{y}\prod_a{\psi(x_a,y_a)}$,则$p(y|x)=\frac{1}{Z(x)}\prod_a{\psi_a(x_a,y_a)}$
条件随机场
给定输入随机变量x,求解条件概率$p(y|x)$的概率无向图模型
序列标注时,特化为线性链条件随机场,输入输出随机变量为等长的两个序列
例如:
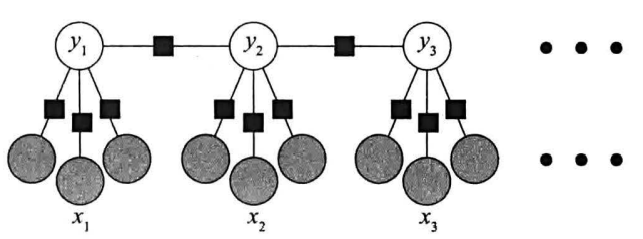
灰色节点代表特征(这里表明每个$x_i$有三个特征)
黑色方块为因子节点,视为特征函数$f_k(y_{t-1},y_t,x_t)$,其中只利用$x_t,y_t$的称为状态特征,利用了$y_{t-1}$的称为转移特征
线性链条件随机场定义如下:
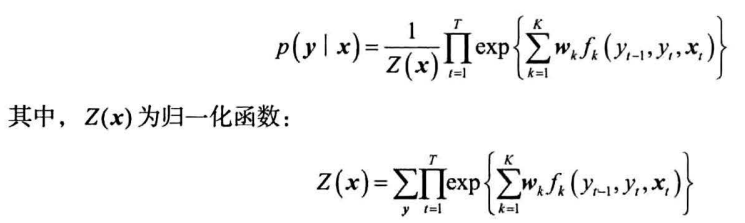
- 需要遍历所有可能的标注序列,即使是非法的
将特征函数和权重写作向量形式,则简化为:
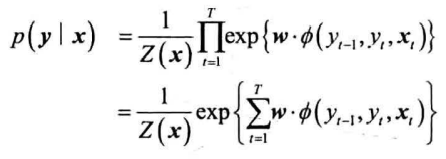
对比结构化感知机的打分函数可知:
- 感知机打分函数与此式的指数部分一致
- 条件随机场和结构化感知机的特征函数一致
- 结构化感知机对某预测打分高,则随机场对其的预测概率越大
- 结构化感知机和条件随机场的预测算法一致,均为维特比算法
训练条件随机场:略
对比结构化感知机:
- 特征函数、权重向量、打分函数、预测算法一致
- 训练算法不同——这是二者准确率差异的唯一原因
- 感知机为在线学习,每次参数更新只使用一个训练实例,没有考虑整个数据集;感知机奖励正确答案对应的特征函数,但只惩罚错得厉害的特征函数
- 条件随机场的对数似然函数和梯度,定义在整个数据集上,每次参数更新都经过全局的考虑;奖励正确的特征函数,惩罚所有错误结果对应的特征函数(虽然惩罚总量不变,但根据模型赋予每个答案的概率,分摊惩罚力度)
工具包:略

