《自然语言处理入门》阅读笔记(5) 第十章+第十一章
文本聚类
文档层级、划分聚类
聚类:将给定对象的集合划分为不同子集,各个子集内部元素尽量相似;子集又称簇,一般没有交集
- 硬聚类:每个元素确定地归入一个簇
- 软聚类:每个元素与每个簇都有从属关系,程度不同
- 划分式聚类算法:结果是一系列不相交的子集
- 层次化聚类算法:结果是一棵树,叶子为元素,父节点为簇
文本聚类流程:特征提取+向量聚类
文档的特征提取
- 词袋(bag-of-words):
- 文档视为一个装有词语的袋子,根据每种词语的计数等统计量,将文档表示为向量
- 其他统计量:
- 布尔词频
- TF-IDF:上一章有阐述,考虑了每个词语的倒序词频
- 词向量
- 其他无监督生成文档向量的方法:自动编码器、受限的玻尔兹曼机等
- 本书以词频作为统计指标,以词袋模型提取文档特征向量
- 定义n个文档的集合为S,第i个文档的特征向量为$\pmb{d}_i=(TF(t_1,d_i),…,TF(t_m,d_i))$,$t_j$表明词表中第j种单词,m为词表大小,$TF(t_j,d_i)$为单词$t_j$在文档$d_i$的出现次数,最后缩放向量使得$||\pmb{d}||=1$
k-means
给定n个向量和一个整数k,找到k个簇$S_1…S_k$和各自的质心$c_1…c_k$,使得下式最小:需要最小化的函数称为准则函数
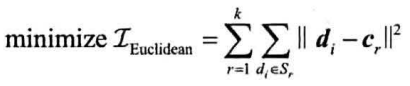
最小化每个向量到质心的欧拉距离的平方和为准则
质心计算:簇内数据点的几何平均:第一个式子为簇内所有向量的和
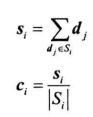
过程:
- 选取k个点作为初始质心
- 所有点分配到最近质心所在的簇
- 计算每个簇的质心
- 重复2和3,直到质心不再变化
不保证收敛到全局最优,但可以局部最优
关键:初始质心的选取,两点距离的度量
- 朴素实现通过随机选取确定初始质心
- 优化:将质心的选取也作为优化的部分,即先随机选取一个数据点作为质心,计算准则函数,保存一个数组维护每个点到最近质心的距离的平方。选取准则函数值的一部分作为标准,遍历所有数据点,若该点到最近质心的距离的平方小于此标准,则添加到质心列表中,同时更新准则函数和保存的数组。循环多次,直到凑够k个初始质心
- 获得质心后,将点分配到质心:
- 欧式距离或余弦距离
HanLP使用了更快的准则函数(基于余弦距离)
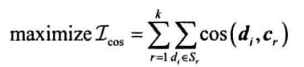
- 数据点从原簇移动到新簇时,上一个准则函数需要重新计算质心,以及两个簇内所有点到新质心的距离
- 这里只需要求原簇和新簇的合成向量即可
- 训练过程如下

重复二分聚类
提高k-means的效率,重复对子集进行二分——每次产生的簇由上到下形成一颗二叉树
- 挑选一个簇进行划分
- 利用k-means将簇划分为两个子集
- 重复1、2,直到产生足够数目的簇
第一步中簇的挑选标准:
- 簇的体积最大
- 簇内元素到质心的相似度最小(距离最大)
- 二分后准则函数的增幅最大
- 每产生一个新簇,都将其二分并计算准则函数的增幅
- 对增幅最大的簇二分,重复多次
自动判断聚类数目
- 设定准则函数的增幅阈值$\beta$,来自动判断k——此时不用人工指定
- 此时的停止条件:所有簇都不可再分,即所有簇的二分增幅都小于$\beta$
标准化评估
P、R、F1
给定:n为文档总数,簇j和其类别i,$n_{ij}$表明簇j中类别为i的文档数目,$n_j$为簇j的文档总数,$n_i$表明类别为i的文档总数
对每种$i,j$的组合,计算:
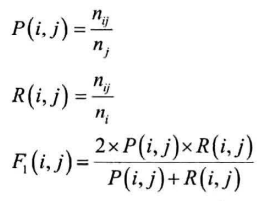
F1简化为一个综合的F1:
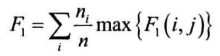
语料库:搜狗实验室的语料库,分为5个类,每个类由1000个文章
文本分类
一个文档属于多个类别:多标签分类
语料库:搜狗实验室的语料库
分类流程:特征提取+分类器处理
文本分类的特征提取
- 这里依旧使用词袋向量作为特征向量,且为词语的频次或TF-IDF向量
- 许多单词对分类决策帮助不大:
- 使用停用词表过滤
- 使用卡方非参数检验过滤
- 计算每个特征(词语)的卡方值
- 去掉卡方值小于10.83的特征——对应p值为0.001
- HanLP中提取TF特征
朴素贝叶斯分类器
联合概率转为条件概率,利用特征条件独立假设简化条件概率的计算
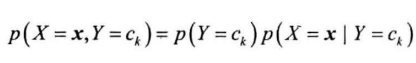
前面通过统计每个类别下的样本数获得
后面假设所有特征条件独立,即:
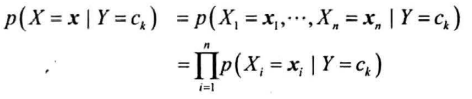
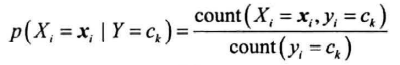
获得以上概率后,训练结束
预测时,根据贝叶斯公式找到使后验概率$p(Y=c_k|X=\pmb{x})$最大的类别即可
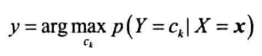
即为:
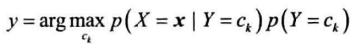
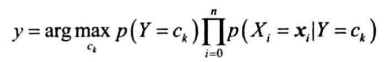
支持向量机分类器
一种二分类模型,找到一个决策边界,使得边界到正负样本的最小距离都最远
线性支持向量机:决策边界为超平面$w\cdot x+b=0$
定义样本点$(x^{(i)},y)$到超平面的距离为几何间隔:
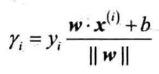
数据集的几何间隔为所有样本点的几何间隔最小值:
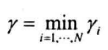
线性支持向量机需要最大化所有样本点的几何间隔最小值,即下面的约束最优化问题:
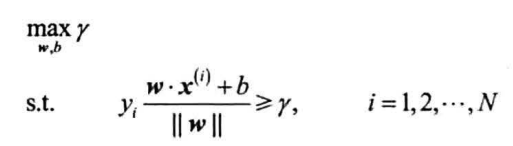
定义函数间隔,取其为1,得到:
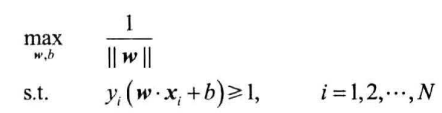
最大化$\frac{1}{||w||}$等价于最小化$\frac{1}{2}||w||^2$,从而等价于:
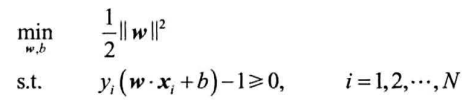
利用拉格朗日法得到最优解$w^、b^$,得到分类决策函数:
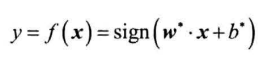
标准化评估
指标为P、R、F(对于每个分类的指标,反应对某一类别的分类性能):
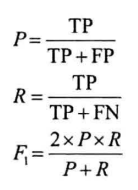
整体性能:将所有类目下的TP、FP、FN求和后,计算上述指标
情感分析
同上类似
词袋模型丢失了词序,并且无法处理一些否定词或双重否定的句子,一种方案为用n元语法保留一些词序

