More Than Code

Chunk-Level Password Guessing

发表于 分类于
本文字数： 3.3k 阅读时长 ≈ 3 分钟

《Chunk-Level Password Guessing: Towards Modeling Refined Password Composition Representations》（CCS 2021）

摘要

  • 经验显示，文本密码存在微妙的内部模式（pattern），例如“4ever”，“ing”，这些模式是密码猜测SOTA模型无法理解的
  • 本文将密码视为几个组块（chunk）的组合，一个组块是频繁出现在一起的字符序列
  • 本文提出一种密码分段方法，能够将密码自动地分块，分别用Markov、PCFG、FLA建立三个chunk级的猜测模型
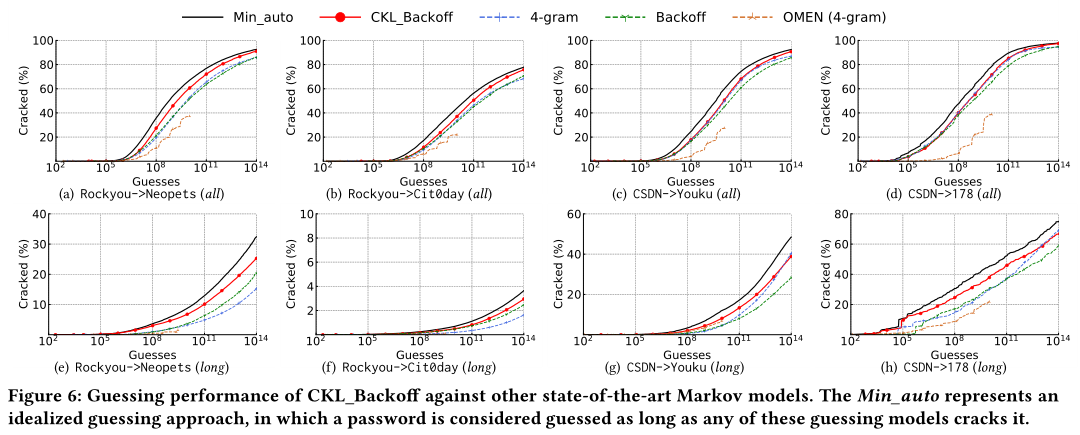
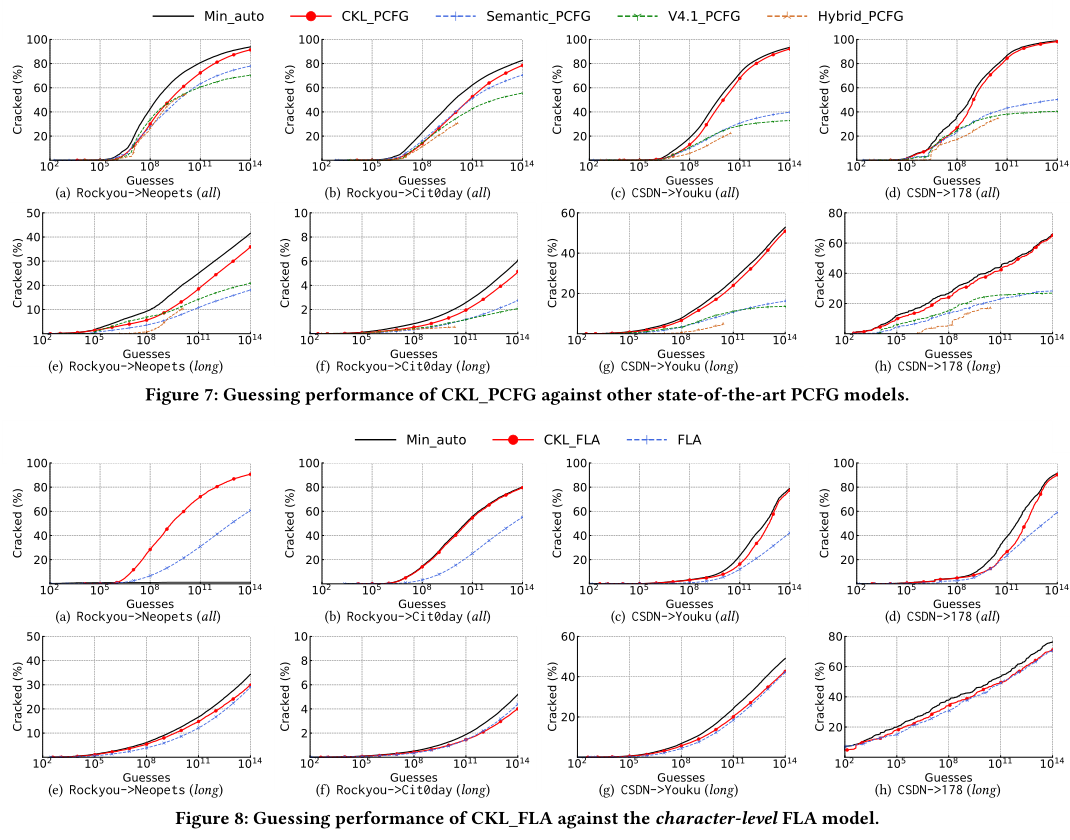
  • 本文在2.5亿条密码上评估了本文方法，结果显示，chunk-level模型的性能分别提高5.7%、51.2%和41.9%
  • 本文认为，密码中公共组块的存在使得密码更容易被攻击，因此本文开发了一个部署在客户端的实时密码强度计来评估密码抵抗chunk-level猜测模型攻击的能力

介绍

  • 模型对训练密码的概率分布建模，以生成猜测密码——因此，看待密码的角度会带来不同的建模，包括：

    • 将密码视为一般字符序列（Markov）
    • 将密码视为相同类别字符串的组合（PCFG）
    • 基于自然语言的单词序列（语义分割的PCFG）

  • 用户通常会用一些特殊技巧来生成密码——例如，4ever——以辅助记忆，并满足“强”密码的要求，因此当密码被视为通用文本序列去建模时，很难找到这些合适的密码组成单元

    • 基于字符的模型（Markov、FLA）过于精细
    • 基于模式的模型（PCFG）过于粗糙

  • 大量现有工作基于人工定义规则、与密码无关的知识（如，单词）来进一步优化密码的表征，例如Backoff Markov将频率高于阈值的最长字符序列视为一个单元，并逐步往后退；Veras提出语义PCFG，以更细粒度切分——但密码中微妙的pattern和自然语言存在差异

  • chunk时频繁出现在一起的字符序列，通过统计获得（例如，“p@ssw0rd4ever”分为两个chunk）

  • 本文提出一种特定于密码的分段方法（termed PwdSegment），可以学习密码中的chunk并建立三种chunk-level的密码猜测模型

    • PwdSegment扩展了BPE算法，密码能被自动分解为多个chunk
    • 基于此，本文建立基于Backoff的chunk-level Markov模型、chunk-level的PCFG、chunk-level的FLA
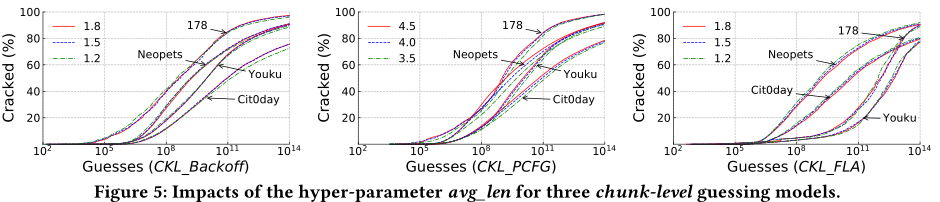
    • CKL Backoff和CKL FLA用较短的chunk（平均长1.8个字符）来替换密码字符，CKL PCFG用较长的chunk（平均4.5个字符）来替换密码字符

  • 本文定量研究了几个安全相关因素和密码强度的关系

    • 本文发现密码中常见chunk的频率是比字符多样性更好的密码强度指标
    • 本文将CKL PCFG压缩，以部署到客户端实现Password Meter

预备知识和密码chunk

威胁模型

  • 量化密码破解需要的猜测次数
  • 离线攻击依据概率降序生成候选密码

数据集

  • 使用6个泄露密码集，超过2.5亿条纯文本密码

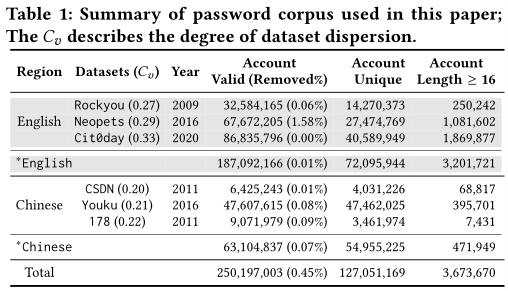
    image-20220228220944571

  • 删除非ascii密码和超过32位的长密码——附录中评估了这些长密码

  • 用变异系数$C_v$来统计每个数据集的复杂度，其值和数据集分散程度成比例

PwdSegment

  • PwdSegment训练一个基于纯文本密码的BPE算法，以获得chunk字典——这一思想源于WordSegment工具

  • BPE算法将生僻的词拆分为多个单元，并保证常用词的完整性：

    • BPE先在纯文本上训练，接着迭代地合并最常见的tokens和新的（unseen）token，最终构成subword字典

    • 每次合并操作，通过用新的subword（例如“w0”）替换最频繁出现的字符对（例如“w”、“0”），来产生新的chunk

    • 根据超参数，重复一定次数的合并操作，将产生成比例大小的chunk字典

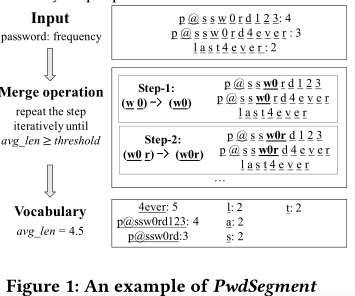
      image-20220301181333331

  • 使用chunk的平均长度（avg_len）代替合并操作的次数，扩展了BPE算法：PwdSegment计数字符对，在生成的chunk的avg_len等于或超过阈值长度时停止合并，如Figure 1所示

    • Setup：准备一组纯文本密码训练集，配置avg_len
    • Input：对密码计数，并分割为字符列表（例如，“p@ssw0rd123”出现4次，则其输入为“p @ s s w 0 r d 1 2 3: 4”）
    • Merge操作：按频率降序迭代合并字符对。第一轮迭代，将出现频率最高（7次）的字符对“w, 0”合并为“w0”。虽然“p, @”也出现了7次，但这里用字典序来合并字符对。第二轮迭代，出现频率最高的字符对为“w0, r”合并为“w0r”，以此类推
    • 生成一个chunk：重复以上步骤，直到chunk的平均长度大于等于阈值。最后，PwdSegment根据chunk字典分割密码

Chunk的属性分析

chunks与自然语言中单词的差异

image-20220302155501249
  • 本文列出top 150的单词和阈值为4.5的chunk
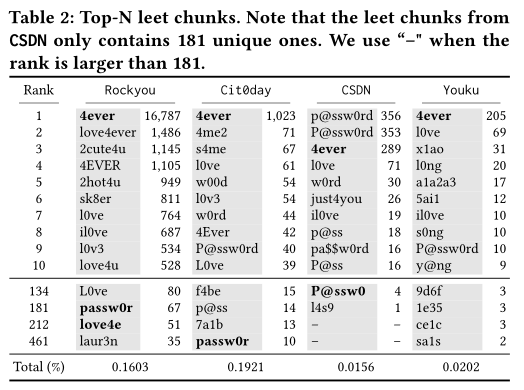
  • 数字对chunk的贡献较大，并且还表现出一定的记忆模式，包括leet、syllable、keyboard、date（还分析了这些模式的比例）
  • 存在一些不完整的语块，例如passw0rld
  • 其他的发现略
image-20220302162237982

chunk的part of speech分布

  • 比较密码字母的词性分布（利用NLTK）
  • 密码更可能包含名词、形容词，动词和副词更少

遵循齐夫定律

  • 密码的齐夫定律有两种变体：PDF-Zipf、CDF-Zipf，如果丢弃尾部密码则密码频率遵循PDF-Zipf，完整密码遵循CDF-Zipf
  • chunk同样可以由PDF、CDF-Zipf定律建模（KS检验结果的值比较低）

Chunk-level猜测模型

全串马尔可夫模型

  • 马尔可夫模型概念略

  • 传统的char-level backoff Markov

    • 为解决稀疏性和顺序选择问题，引入backoff机制
    • 例如，前缀是“p@ssw0r”，用整个前缀来确定下一个字符要更加准确。如果前缀很少出现，例如“a#!Dce”，则触发Backoff，仅使用较短的前缀来估计下一个字符
    • Backoff选择一个阈值，使用出现次数高于此阈值的最长前缀，来估计下一个字符。如果低于此阈值，换一个较短的前缀——如果使用较短的前缀，则其概率应当被标准化

  • chunk-level：

    • 用一个chunk，而不是一个字符来作为转移概率计算的基本单位

    • 设定了前缀chunk的数目阈值，而不是默认选择最多的前缀chunk

    • 给定计数阈值$\phi$，和最大前缀数目阈值$\chi$，定义$ck_i$代表组成密码的第$i$个chunk，$\lambda_{i,j}$表示$ck_i$到$ck_j$之间的密码字串（包括它们），因此有：

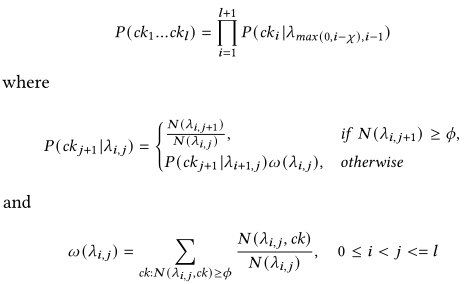
      image-20220302173402618

  • 同样的，设置一个start和一个end的chunk（只代表起始和终止）

  • 举例：“p @ s sw 0 r d 4 ever

    • $\phi$为10，$\chi$为7

    • 假设除了第9个chunk（ever）的最长前缀$\lambda_{i,j}$之外的其他最长前缀计数都大于$\phi$，则应当从当前最长前缀逐步减少，触发backoff机制。假设”ever“满足大于阈值的较短前缀chunk长度为6，此时密码的概率为：

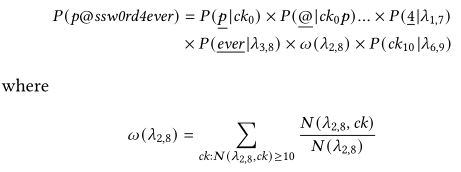
      image-20220302182212431

    • 参数设置：$\phi=10$，$\chi=5$，avg_len=1.8

基于模板的PCFG模型

  • PCFG原理略

  • 标签含义：

    • L、U、F、S：小写字母、大写字母、数字、符号
    • DM：由两种类型字符组成，例如 4ever
    • TM：由三种字符组成，例如 p@ssw0rd
    • FM：由四种字符组成，例如 P@SSw0RD

  • 举例：p@ssw0rd 4ever

    • 可以分割为$TM_8DM_5$，此时的概率为：

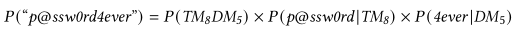
      image-20220302190004628

  • CKL_PCFG通过用从训练集里学到的相同长度实例，替换标签，以生成候选密码，并降序输出候选密码

  • 参数设置：avg_len为3.5

FLA模型

  • 同理，用较短的chunk，替代字符

  • CKL_FLA被训练成，在给定先前块的上下文时，输出下一个块的概率分布

  • 枚举所有概率高于给定阈值的密码

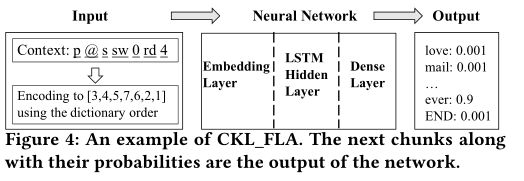
    image-20220302190436200

  • 举例：p @ s sw 0 r d 4ever

    • 给定前面的chunk序列，依据chunk字典编码
    • 输入网络，决定下一个chunk为4ever
    • 再次输入网络，下一个chunk为结束符，则输出生成的密码

  • 参数设置：大多数超参数和原本的FLA相同，使用两个隐藏层，添加64维的嵌入层；全连接层为128，avg_len取1.8

评估

image-20220302184454653

image-20220302184519413

image-20220302184555286

相关文章推荐