MIT-6.830 Lab3 总结与备忘
实现一个查询优化器(一个选择性估计框架
selectivity estimation framework,或者一个基于成本的优化器cost-based optimizer)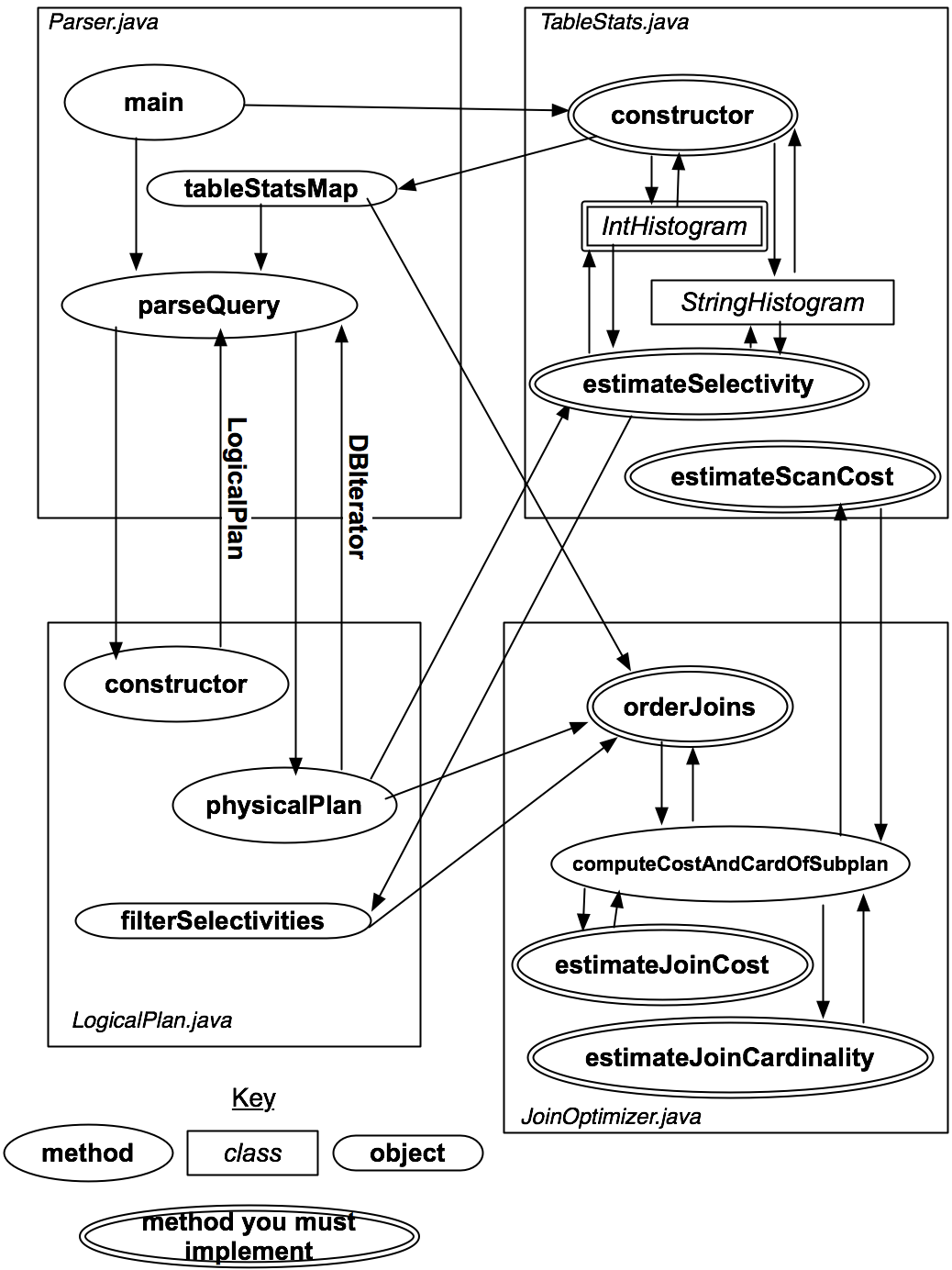
SimpleDB的查询优化器使用CBO(cost-based optimizer),核心思想是根据表的统计信息,估算不同查询计划的代价。查询计划的代价与基数(select和join语句返回的数据条数)、选择性(过滤的记录比例)有关
Parser被调用时会计算所有表的统计信息,收到查询语句时,Parser把查询转换为逻辑执行计划再调用查询优化器生成优化后的执行计划
这里只关注join的顺序,以及访问原始table的成本,不关注额外运算的成本
具体开销由I/O开销和CPU开销两部分组成(
ntups(t1)是表t1的tuple的数量)1
2
3joincost(t1 join t2) = scancost(t1) + ntups(t1) x scancost(t2) //IO cost
+ ntups(t1) x ntups(t2) //CPU cost
Here, ntups(t1) is the number of tuples in table t1.对于一个left-deep Join plan,如:
p = t1 join t2 join ... tn,其查询成本为scancost(t1) + scancost(t2) + joincost(t1 join t2) + scancost(t3) + joincost((t1 join t2) join t3) + ...,其中scancost(t1)代表扫描表t1需要的磁盘IO,joincost(t1, t2)代表t1和t2进行join需要耗费的CPU时间,为了使I/O和CPU成本具有可比性,通常使用一个恒定的比例系数ntups的值能通过遍历一遍table得到,对于有多个谓词的table,ntups的估计可以使用选择性估计,借助直方图实现:
- 计算一个表的某字段最大值、最小值
- 为每个字段构造直方图,NumB为直方图的bucket数目,每一个bucket代表数据(record)的该字段落在这个字段范围的数目(类似于轮盘赌,或者说每个直方代表一个桶)
- 对于一个表达式f=const的选择性,要计算包含值const的bucket。假设这个bucket宽度w,高度h(tuple数目),表有ntuples,则占比计算大致为(h/w/tuples)
- 对于一个表达式f>const的选择性,如果b_part代表const在b上占据的部分,则b_part可以表示为 (b_right - const / w_b),则b bucket选择性大致为 (h_b/ntups) * (b_right-const) / w_b。同时,还要将b bucket后面的筒贡献的选择性相加
- 对于其他表达式的选择性,以此类推
- 感觉上,其实就是大于某个值的区间里的tuple数量/总的tuple数量
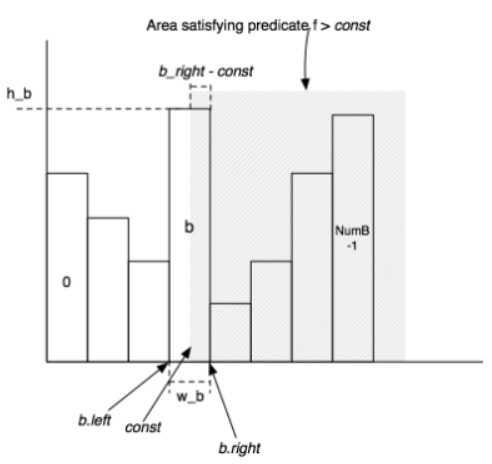
exercise1实现对某一字段直方图的构建
exercise2实现对某一表的所有字段的直方图的构建
exercise3实现对连接代价以及连接操作后基数的估计
exercise4实现查询优化,给定连接查询,选择出连接代价最小的查询
Exercise 1
思路整理
完成
optimizer/IntHistogram.java,通过IntHistogramTest单元测试数据定义为位于min~max之间的N个等宽(w_b)的bucket
1
2selectivity = (h/w) / ntup, f=const
selectivity = (h_b/ntups) * (b_right-const) / w_b, f>constIntHistogram的构造函数给出了最大值、最小值以及设置的bucket数目,因此只用赋值给对应的属性,并建立一个保存直方图数据的列表
addValue(int v):需要注意v的范围
avgSelectivity():求平均值
double estimateSelectivity(Predicate.Op op, int v):计算bucket的左右边界
具体实现
width设置:
(max - min + 1.0) / buckets给定一个值,求其所在bucket的index:
(int) ((v - this.min) / width)estimateSelectivity:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43/**
* Estimate the selectivity of a particular predicate and operand on this table.
* <p>
* For example, if "op" is "GREATER_THAN" and "v" is 5,
* return your estimate of the fraction of elements that are greater than 5.
*
* @param op Operator
* @param v Value
* @return Predicted selectivity of this particular operator and value
*/
public double estimateSelectivity(Predicate.Op op, int v) {
// some code goes here
switch (op) {
case EQUALS:
return this.estimateSelectivity(Predicate.Op.GREATER_THAN, v - 1)
- this.estimateSelectivity(Predicate.Op.GREATER_THAN, v - 1);
case LESS_THAN:
return 1.0 - this.estimateSelectivity(Predicate.Op.GREATER_THAN_OR_EQ, v);
case LESS_THAN_OR_EQ:
return 1.0 - this.estimateSelectivity(Predicate.Op.GREATER_THAN, v);
case GREATER_THAN_OR_EQ:
return this.estimateSelectivity(Predicate.Op.GREATER_THAN, v - 1);
case GREATER_THAN:
if (v <= this.min) {
return 1.0; // 此时整个直方图都算进去
} else if (v > this.max) {
return 0.0;
} else {
int index = (int) ((v - this.min) / this.width);
double sum = 0.0;
for (int i = index + 1; i < buckets.length; i++) {
sum += buckets[i];
}
double indexCoverage = buckets[index] * ( // v所在的bucket中,大于等于v的tuple数目
(min + (index + 1) * width - v - 1) / width
);
return (sum + indexCoverage) / this.numTuples;
}
case NOT_EQUALS:
return 1.0 - this.estimateSelectivity(Predicate.Op.EQUALS, v);
}
return 0.0;
}
Exercise 2
思路整理
完成
optimizer/TableStats.java,通过TableStatsTest单元测试TableStats类包含计算一个表中tuples和Page数目的方法,以及估计该表字段上谓词选择性的方法(后面exercise中创建的查询分析器,为每个表创建一个TableStats实例,并将这些结构传递给查询优化器),这里所谓“字段上谓词选择性”,其实就是给定一个谓词,表中指定字段满足谓词的tuple数目
public TableStats(int tableid, int ioCostPerPage):构造直方图,需要min, max——顺序扫描表,确定每个字段的min, max值,再从头扫描一次加载实际数据。为了方便,添加几个私有属性:1
2
3
4
5
6
7
8
9private int numTuples;
private DbFile dbFile;
private int[] min; // 保存不同field index对应的最小值
private int[] max; // 保存不同field index对应的最大值
private HashMap<Integer, IntHistogram> intHistogramHashMap; // 保存不同field index对应的intHistogramHashMap
private HashMap<Integer, StringHistogram> stringHistogramHashMap;int totalTuples():返回构造函数中记录的totalTuplesestimateSelectivity(int field, Predicate.Op op, Field constant):估计表第field个字段的在谓词Op下的选择性estimateScanCost():估计扫描全表代价,使用构造时传入的ioCostPerPage计算estimateTableCardinality(double selectivityFactor):估计表基数,将numTuple乘参数selectivityFactor就行一些接口方法不太好找(比如,想获得一个field的值,需要将field接口转为相应类,这个相应类的名字不好找,得翻看其他文件夹)
exercise 2相当于exercise 1的上层调用,给定一个表,对每个字段构建直方图,然后根据直方图计算扫描这个表的cost(此时就调用了exercise 1实现的各种方法)
Cardinality是一个数据库里面的一个术语(这里为某列不同取值的个数),分为:
- Base Cardinality 指表中记录的数量
- Effective cardinality 指对表查询操作返回的记录数量
- Join cardinality 指在存在join连接的情况下,返回的记录数量
- Distinct cardinality 指数据集中某列不同取值的个数
- Group cardinality 指group查询语句返回的记录数量
具体实现
构造函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71public TableStats(int tableid, int ioCostPerPage) {
this.tableid = tableid;
this.ioCostPerPage = ioCostPerPage;
this.dbFile = Database.getCatalog().getDatabaseFile(tableid);
int numFields = this.dbFile.getTupleDesc().numFields();
this.max = new int[numFields]; // 建立max数组,并初始化
this.min = new int[numFields];
for (int i = 0; i < numFields; i++) {
this.max[i] = Integer.MIN_VALUE;
this.min[i] = Integer.MAX_VALUE;
}
this.stringHistogramHashMap = new HashMap<>();
this.intHistogramHashMap = new HashMap<>();
// 开始扫描这个DbFile
try {
SeqScan scan = new SeqScan(new TransactionId(), this.tableid);
scan.open();
while (scan.hasNext()) {
Tuple curTuple = scan.next(); // 获得下一个Tuple
for (int i = 0; i < numFields; i++) {
// 检查字段的类型,如果不是StringType就更新最大值和最小值
if (!curTuple.getField(i).getType().equals(Type.STRING_TYPE)) {
IntField curField = (IntField) curTuple.getField(i);
int value = curField.getValue();
this.max[i] = Math.max(this.max[i], value);
this.min[i] = Math.min(this.min[i], value);
}
}
this.numTuples += 1;
}
scan.close();
} catch (DbException | TransactionAbortedException e) {
e.printStackTrace();
}
// 实例化各个field的直方图类
for (int i = 0; i < numFields; i++) {
if (this.dbFile.getTupleDesc().getFieldType(i).equals(Type.STRING_TYPE)) {
// field为STRING_TYPE
this.stringHistogramHashMap.put(i, new StringHistogram(NUM_HIST_BINS));
} else {
// field为INT_TYPE
this.intHistogramHashMap.put(i, new IntHistogram(NUM_HIST_BINS, this.min[i], this.max[i]));
}
}
// 向各个field的直方图填充数据
try {
SeqScan scan = new SeqScan(new TransactionId(), this.tableid);
scan.open();
while (scan.hasNext()) {
Tuple curTuple = scan.next(); // 获得下一个Tuple
for (int i = 0; i < numFields; i++) {
// 检查字段的类型,填充数据
if (!curTuple.getField(i).getType().equals(Type.STRING_TYPE)) {
this.intHistogramHashMap.get(i).addValue(((IntField) curTuple.getField(i)).getValue());
} else {
this.stringHistogramHashMap.get(i).addValue(((StringField) curTuple.getField(i)).getValue());
}
}
}
scan.close();
} catch (DbException | TransactionAbortedException e) {
e.printStackTrace();
}
}此外测试的时候发现并修复之前page淘汰的一个bug,以及上一个exercise的
estimateSelectivity()的bug
Exercise 3
思路整理
完成
optimizer/JoinOptimizer.java,通过单元测试JoinOptimizerTest的estimateJoinCostTest和 estimateJoinCardinality回到最开始,要获得一次join的成本,需要预估t1 join t2的ntups。此时:
- 对于等值查询(Op为Equals),如果有某个为主键,则结果集规模小于等于非主键表;如果没有主键,则大小可能为两个表大小乘积,也可能为0,可以简单地预估为大表的tuple数
- 对于范围扫描查询(Op不是Equals),可以估计为笛卡尔积的30%
JoinOptimizer包含所有用于排序和计算连接成本的方法
estimateJoinCost(LogicalJoinNode j, int card1, int card2, double cost1, double cost2):估计连接计划 j 的成本,左边输入是cardinality card1,右边输入是cardinality card2,扫描左边输入的成本是cost1,访问右边输入的成本是card2——这里应用最开始的公式即可,scancost(t1)为cost1,ntups(t1)为card1estimateJoinCardinality(LogicalJoinNode j, int card1, int card2, boolean t1pkey, boolean t2pkey):估计连接 j 输出的tuples数,左边输入大小为card1,右边输入大小为card2,左边和右边字段是否为主键的标志t1pkey和t2pkey
具体实现
根据公式,以及lab介绍的表述:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37public double estimateJoinCost(LogicalJoinNode j, int card1, int card2,
double cost1, double cost2) {
if (j instanceof LogicalSubplanJoinNode) {
// A LogicalSubplanJoinNode represents a subquery.
// You do not need to implement proper support for these for Lab 3.
return card1 + cost1 + cost2;
} else {
// Insert your code here.
// HINT: You may need to use the variable "j" if you implemented
// a join algorithm that's more complicated than a basic
// nested-loops join.
return cost1 + card1 * cost2 + card1 * card2;
}
}
public static int estimateTableJoinCardinality(Predicate.Op joinOp,
String table1Alias, String table2Alias, String field1PureName,
String field2PureName, int card1, int card2, boolean t1pkey,
boolean t2pkey, Map<String, TableStats> stats,
Map<String, Integer> tableAliasToId) {
int card = 1;
// some code goes here
if (joinOp.equals(Predicate.Op.EQUALS)) {
if (!t1pkey && !t2pkey) {
card = Math.max(card1, card2);
} else if (t1pkey && t2pkey) {
card = Math.min(card1, card2);
} else if (t1pkey) {
card = card1;
} else {
card = card2;
}
} else {
card = (int) (0.3*card1*card2);
}
return card <= 0 ? 1 : card;
}这个应该相比exercise2在更高一层
Exercise 4
思路整理
完成
optimizer/JoinOptimizer.java中,实现方法List<LogicalJoinNode> orderJoins(Map<String, TableStats> stats, Map<String, Double> filterSelectivities, boolean explain),通过单元测试JoinOptimizerTest和系统测试QueryTest。以上实现了如何估计一个join的成本,这个exercise会实现Selinger优化器。这里,join被表达为一个连接节点的列表(例如,predicates over two tables),伪代码为
1
2
3
4
5
6
7
8
9
10
111. j = set of join nodes
2. for (i in 1...|j|):
3. for s in {all length i subsets of j}
4. bestPlan = {}
5. for s' in {all length d-1 subsets of s}
6. subplan = optjoin(s')
7. plan = best way to join (s-s') to subplan
8. if (cost(plan) < cost(bestPlan))
9. bestPlan = plan
10. optjoin(s) = bestPlan
11. return optjoin(j)已经提供了几个类和方法来实现这个算法
JoinOptimizer.java的enumerateSubsets(List v, int size)返回一个大小为v的所有子集的集合,虽然对于大型集合来说效率非常低。可以通过实现一个更有效的枚举器来获得额外的分数(提示:可以考虑实现一个更有效的枚举器,使用原地生成算法和懒惰迭代器(或流)接口来避免直接计算整个幂集)——伪代码第三行computeCostAndCardOfSubplan方法:给定一个连接的子集(joinSet),一个要从该子集移除的连接(joinToRemove),方法计算出将joinToRemove连接到joinSet的最佳方法——计算在已求出的集合的最优排列上,join一个新元素的最佳方式- 返回一个CostCard对象,属性包括成本、cardinality、最佳连接顺序(一个列表),如果找不到最佳方式,或者所有计划的成本都大于参数bestCostSoFar,可能返回null
- stats和filterSelectivities来自orderJoins方法的参数
- 执行伪代码第6-8行
1
2
3
4
5
6private CostCard computeCostAndCardOfSubplan(Map<String, TableStats> stats,
Map<String, Double> filterSelectivities,
LogicalJoinNode joinToRemove,
Set<LogicalJoinNode> joinSet,
double bestCostSoFar,
PlanCache pc)printJoins:显示join plan的图形表示1
2
3
4private void printJoins(List<LogicalJoinNode> js,
PlanCache pc,
Map<String, TableStats> stats,
Map<String, Double> selectivities)PlanCache类:缓存连接子集的最佳方式(computeCostAndCardOfSubplan需要它的一个实例)
orderJoins方法应该在joins类成员上操作,返回一个连接顺序的列表。列表第0项表示left-deep plan中最左、最底的连接,相邻的连接至少共享一个字段stats可以找到查询的FROM列表中给定表名的TableStats
filterSelectivities可以找到表的任何谓词的选择性(保证FROM列表中的每个表有一个条目)
explain指定应该输出一个连接顺序的表示,以供参考
left-deep:
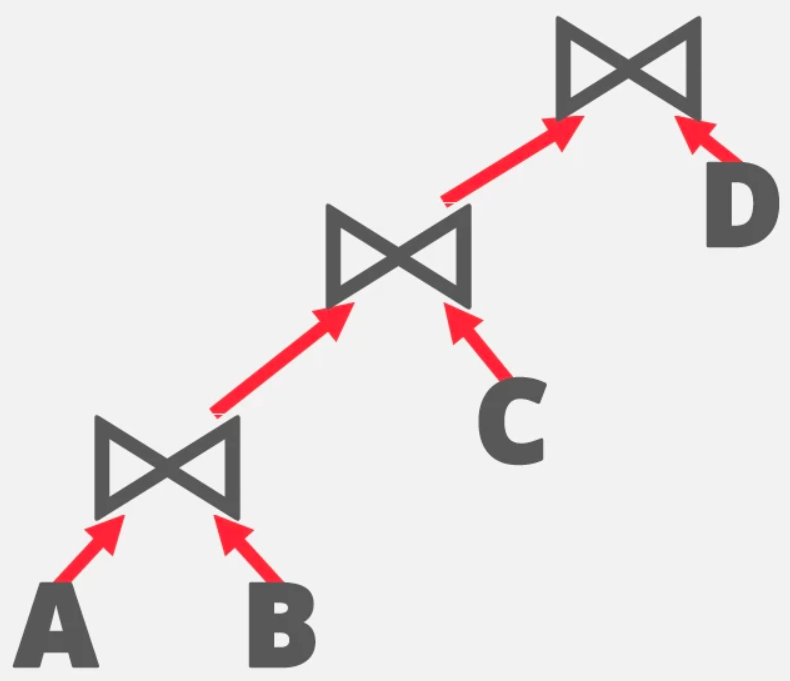
Selinger optimizer
- 对于有N个Join的式子,适当的先后顺序能更快速完成join
- 对于一个Join最少的cost,就是其本身,保存到Cache
- 对于两个Join,AB和BA是两种不同的cost,算出最优的结果,保存到Cache
- 对于三个Join,
A{BC}和{BC}A在对比时,可以看到BC最优的结果已经在Cache里面了,此时只需要比较A应该放前面还是后面,其余同理
具体实现
代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49/**
* Compute a logical, reasonably efficient join on the specified tables. See
* PS4 for hints on how this should be implemented.
*
* @param stats Statistics for each table involved in the join, referenced by
* base table names, not alias
* @param filterSelectivities Selectivities of the filter predicates on each table in the
* join, referenced by table alias (if no alias, the base table
* name)
* @param explain Indicates whether your code should explain its query plan or
* simply execute it
* @return A List<LogicalJoinNode> that stores joins in the left-deep
* order in which they should be executed.
* @throws ParsingException when stats or filter selectivities is missing a table in the
* join, or or when another internal error occurs
*/
public List<LogicalJoinNode> orderJoins(
Map<String, TableStats> stats,
Map<String, Double> filterSelectivities, boolean explain)
throws ParsingException {
// some code goes here
PlanCache cache = new PlanCache();
CostCard bestCostCard = new CostCard();
for (int i = 1; i < joins.size() + 1; i++) { // 伪代码中,i从1到|j|
Set<Set<LogicalJoinNode>> subsetJoinNodes = enumerateSubsets(joins, i);
for (Set<LogicalJoinNode> subset : subsetJoinNodes) {
double best = Double.MAX_VALUE;
for (LogicalJoinNode joinNode : subset) {
CostCard costCard = this.computeCostAndCardOfSubplan(
stats,
filterSelectivities,
joinNode,
subset,
best,
cache
);
if (costCard == null) {
continue;
}
best = costCard.cost;
bestCostCard = costCard;
}
if (best != Double.MAX_VALUE) {
cache.addPlan(subset, best, bestCostCard.card, bestCostCard.plan);
}
}
}
return bestCostCard.plan;
}exercise4挺难理解的,特别是伪代码不是那么清楚,要靠函数的参数类型去猜自己还有什么没写的
有时间还需要结合系统测试Query和几个单元测试,把这个lab再过一遍。有些概念和流程还是不太清楚

